Уравнение и график рыночной линии (CML). Уравнение и график линии ценной бумаги (SML)
В отличие от модели рынка, постулирующей исключительную роль характеристик рыночного портфеля при определении доходности отдельных рисковых активов, CAPM обосновывает это положение.
Из теоремы сепаратности теории портфеля следует, что у всех покупателей акций структура спроса одинакова; хотя размеры портфелей у инвесторов различны, все они хотят иметь одинаковый ассортимент рисковых активов. Для обеспечения равновесия на рынке рисковых ценных бумаг необходимо, чтобы структура предложения совпадала со структурой портфеля, определяемой на рис. 5.16 точкой M - точкой касания прямой, проходящей через i с линией области эффективного выбора портфеля. Отсюда вытекает исходное положение CAPM: при равновесии на рынке ценных бумаг рыночный портфель как совокупность всех обращающихся на рынке рисковых активов совпадает с оптимальным для инвесторов портфелем. Поэтому в состоянии равновесия ожидаемая доходность имущества ( 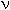 ), определяемая по формуле (5.8), у любого инвестора равна
), определяемая по формуле (5.8), у любого инвестора равна
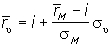 | . | (5.17) |
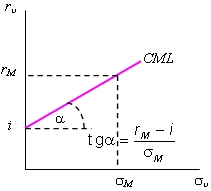
| Уравнение (5.17) получило название уравнения линии рынка капитала CML (capital market line), которая показана на рис. 5.16. Она представляет множество эффективных структур финансовых вложений при равновесии на рынке рисковых ценных бумаг. Это означает, что при равновесии на финансовых рынках имущество рационального инвестора состоит из рыночного портфеля определенного размера и вложений или задолженности на денежном рынке. Угол наклона CML отражает цену риска вложений на рынке рисковых активов: он показывает, на сколько повышается доходность имущества инвестора при увеличении на единицу их риска, который изменяется прямо пропорционально изменению доли рисковых активов в общей сумме имущества. Иначе говоря, tg 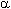 - предельная доходность риска имущества при наличии на рынке рисковых и безрисковых активов - предельная доходность риска имущества при наличии на рынке рисковых и безрисковых активов 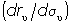 . . |
Можно доказать, что приведенное соотношение у рыночного портфеля акций определяется по формуле
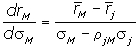 | , |
где 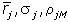 - соответственно ожидаемая доходность, мера риска и коэффициент корреляции некоторого j-го вида рисковых активов.
- соответственно ожидаемая доходность, мера риска и коэффициент корреляции некоторого j-го вида рисковых активов.
Поскольку структура рыночного портфеля определяется точкой касания прямой CML с эффективной областью выбора портфеля, то 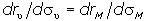 . Поэтому
. Поэтому
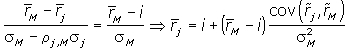 | . | (5.18) |
Второе слагаемое в формуле (5.18) представляет премию за риск: ожидаемая доходность рискового актива j превышает доходность безрисковой ссуды. Если риск измерять посредством ковариации доходностей j-й акции и рыночного портфеля, то 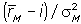 есть цена риска.
есть цена риска.
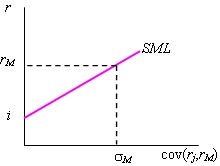
В графическом виде зависимость между ожидаемой доходностью рискового актива и величиной присущего ему риска (формула 5.18) представляется линией рынка ценных бумаг SML (security market line), изображенной на рис. 5.17, а. Она показывает, что между доходностью и риском финансового актива существует положительная линейная зависимость. В отличие от линии CML, которая показывает, как растет ожидаемая доходность имущества по мере роста его риска, линия SML представляет связь между ожидаемой доходностью отдельной акции и ее риском, измеряемым посредством cov 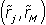 .
.
Обратим теперь внимание на то, что сомножитель, стоящий за скобкой в уравнении (5.18), есть коэффициент 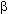 j, характеризующий в модели линейной регрессии взаимозависимость между
j, характеризующий в модели линейной регрессии взаимозависимость между 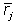 и
и 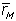 :
: 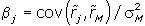 . Поэтому уравнение линии SML можно записать следующим образом:
. Поэтому уравнение линии SML можно записать следующим образом:
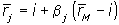 | . | (5.19) |
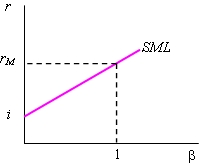
Ее график изображен на рис. 5.17, б.
| Ожидаемую доходность акции за период можно представить в виде
где |
Из формул (5.19) и (5.20) следует, что в модели САРМ
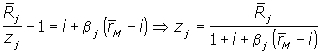 | , | (5.21) |
т.е. цена рискового актива определяется путем дисконтирования ожидаемого от него дохода по рыночной ставке процента, увеличенной на премию за риск.

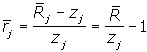
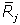 - сумма ожидаемых дивидендов плюс цена акции на конец периода; zj - текущая цена акции.
- сумма ожидаемых дивидендов плюс цена акции на конец периода; zj - текущая цена акции.