Оценка риска актива
В качестве численного показателя риска актива могут использоваться следующие показатели:
• ожидаемая доходность;
• стандартное отклонение;
• коэффициент вариации.
Ожидаемую доходность по каждому активу, являющуюся одной из важнейших характеристик эффективности инвестиций.
То есть ожидаемая доходность актива рассчитывается как, средневзвешенная доходностей при разных будущих состояниях экономики по вероятности наступления этих будущих состояний. Очевидно, что наиболее предпочтительные проекты обладают наибольшей ожидаемой доходностью. Рассчитанная таким образом ожидаемая доходность не является той величиной, которая будет достигнута. Эта величина может рассматриваться как наиболее вероятная или как математическое ожидание доходностей при различных будущих состояниях экономики.
Рассмотрим ряд статистических величин, оценивающих риск и доходность финансовых активов.
Дисперсией, называется мера разброса возможных исходов относительно ожидаемого значения: чем выше дисперсия, тем больше разброс. Для расчета дисперсии дискретного распределения используется следующая формула:
s2 = 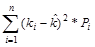 .
.
Поскольку интерпретация термина «процент в квадрате» затруднительна, в качестве другого измерителя разброса индивидуальных значений вокруг среднего часто используется средне, квадратическое отклонение, представляющее собой квадратный корень из дисперсии:
s = 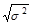 .
.
Как правило, чем выше ожидаемая доходность, тем больше величина среднего квадратического отклонения. Прежде чем использовать s в качестве меры относительного риска инвестиций с различной ожидаемой доходностью, необходимо стандартизировать среднее квадратическое отклонение и рассчитать риск, приходящийся на единицу доходности. Сделать это можно при помощи коэффициента вариации, который представляет собой отношение среднего квадратического отклонения к ожидаемому значению доходности:
CV = 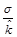 .
.
