Абораторная работа №3 Доходность финансовых операций. 1 страница

абораторная работа №1. Наращение и дисконтирование. Потоки платежей. Ренты.

ариант 1

Вопрос 1. Понятие ставки процента. Сложные проценты.

Вопрос 2. Каким образом учитывается инфляция при вычислении наращенной суммы?

Вопрос 3. Современная величина дискретной ренты при непрерывном начислении процентов

Вопрос 4. Дисконтирование на основе непрерывных процентных ставок. Переменная сила роста.

Задача 1. Найти современную и наращенную величины годовой ренты с , .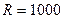

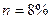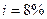Задача 2. Вычислить 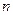- годичную ссуду покупки квартиры за A рублей с годовой ставкой 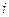процентов и начальным взносом 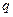процентов. Сделать расчет для ежемесячных и ежегодных выплат.

Расчет провести для следующих данных: 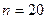; 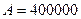руб.;

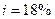
Задача 3. Какая сумма предпочтительнее при ставке сложных процентов 12% : $1000 сегодня или $1500 через 3 года?

Задача 4. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 5 лет с годовым платежом 1000, и другая — 8 лет и платежом 800. Годовая ставка процента 8%.

Задача 5. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 5 лет с годовым платежом 1000, и другая — 8 лет и платежом 800. Годовая ставка процента 8%.

ариант 2

Вопрос 1. Мультиплицирующие и дисконтирующие множители.

Вопрос 2. Современная величина дискретной ренты при непрерывном начислении процентов.

Вопрос 3. Каким образом учитывается инфляция при вычислении наращенной суммы?

Вопрос 4. Дайте определение понятиям «поток платежей», «аннуитет», «наращенная сумма платежей», «современная сумма платежей».

Задача 1. Семья хочет накопить $12000 на машину, вкладывая в банк $1000 ежегодно. Годовая ставка процента в банке 7%. Как долго ей придется копить?

Задача 2. Каждые полгода на банковский счет писателя издательство перечисляет 2000 руб., на которые банк начисляет каждые полгода 7% по схеме сложных процентов. Сколько будет на счете через 4 года?

Задача 3. Определить процентную ставку для 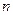- летнего займа в 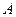рублей с ежегодной выплатой в 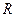рублей. Решить задачу для следующих исходных данных:

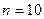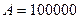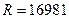лет, руб., руб.

Задача 4. Замените годовую ренту с годовым платежом $600 и длительностью 10 лет семилетней годовой рентой. Ставка процента 8% в год.

Рекомендация. Из уравнения 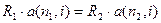находим платеж .

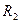Задача 5. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 7 лет с годовым платежом 1500, и другая — 4 года и платежом 1800. Годовая ставка процента 12%.

ариант 3

Вопрос 1. Современная величина годовой ренты с начислением процентов m раз в год.

Вопрос 2. Поток платежей. Основные характеристики.

Вопрос 3. Какие задачи необходимо решить при объединении рент?

Вопрос 4. Дисконтирование на основе непрерывных процентных ставок. Переменная сила роста.

Задача 1. Годовая ставка сложных процентов равна 15%. Через сколько лет начальная сумма увеличится на 50%?

Задача 2. В банк помещен депозит в размере 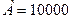руб. По этому депозиту в первом году будет начислено 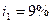, во втором - 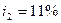, в третьем - 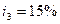, в четвертом и пятом - 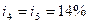. Сколько будет на счету в конце пятого года? Расчеты проведите по схеме простых и сложных процентов.

Задача 2. Замените годовую десятилетнюю ренту с годовым платежом $1000 на ренту с полугодовым платежом по $600. Годовая ставка процента 8%.

Рекомендация. Из уравнения 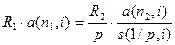находим срок .

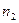Задача 3. У вас есть возможность вложить денежные средства в проект стоимостью 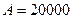. Через год будет возвращено 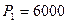, через два года - 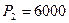, через три года - 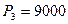, через четыре года 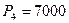. Альтернативный вариант - положить деньги в банк под 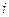процентов годовых. При какой годовой процентной ставке выгоднее вложить деньги в инвестиционный проект?

Задача 4. Покупатель предложил два варианта расчетов при покупке дачи: 1) $5000 немедленно и затем по $1000 в течение 5 лет; 2) $8000 немедленно и по $300 в течение 5 лет. Какой вариант выгоднее при годовой ставке процента: а)10% , б) 5% .

Задача 5. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 5 лет с годовым платежом 1000, и другая — 8 лет и платежом 800. Годовая ставка процента 8%.

ариант 4

Вопрос 1. Принцип неравноценности денег.

Вопрос 2. Дисконтирование по простым и сложным процентам.

Вопрос 3. Понятие номинальной и эффективной ставки, их взаимосвязь.

Вопрос 4. Принцип финансовой эквивалентности обязательств.

Задача 1. Годовая ставка сложных процентов равна 8%. Через сколько лет начальная сумма удвоится?

Задача 2. Рассмотрим годовую ренту при 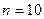, 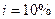. Что более увеличит наращенную величину ренты: увеличение длительности на 1 год или увеличение процентной ставки на 1%?

Задача 3. В банк помещен депозит в размере 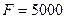руб. По этому депозиту в первом году будет начислено 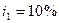, во втором - 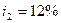, в третьем - 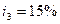, в четвертом и пятом - 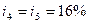. Сколько надо было бы поместить на счет при постоянной процентной ставке 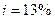, чтобы обеспечить ту же сумму.

Расчеты проведите по схеме простых и сложных процентов.

Задача 4. Провести детальный анализ ренты длительностью 4 года, годовым платежом R = 1000 д.е. и переменной процентной ставкой: 5% во 2-м году, 8% — в 3-м, 10% — в 4-м году. Определить современную величину этой ренты?

Задача 5. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 5 лет с годовым платежом 500, и другая — 4 года и платежом 1800. Годовая ставка процента 9%.

ариант 5

Вопрос 1. Множитель наращения. Соотношение множителей наращения по простым и сложным процентам.

Вопрос 2. Финансовая рента. Основные характеристики.

Вопрос 3. Соотношение между наращенной и современной величинами ренты.

Вопрос 4 Наращенная сумма p-срочной ренты.

Задача 1. 13 января в банк положили сумму 1000 до востребования под ставку 12% годовых сложных процентов. Какую сумму снимет вкладчик 1 сентября?

Задача 2. . Предположим, что Вы заключили депозитный контракт на сумму $10000 на 3 года при 12-и процентной ставке. Если проценты начисляются ежеквартально, какую сумму Вы получите по окончании контракта?

Задача 3. Для ренты с параметрами: годовая ставка процента – 12%, годовой платеж – 400 д.е., длительность ренты – 6 лет, получить следующие ее характеристики: коэффициенты приведения и наращения; современную и наращенную величины.

Задача 4.После внедрения мероприятия по снижению административных издержек предприятие планирует получить экономию $1,000 в год. Сэкономленные деньги предполагается размещать на депозитный счет (под 5 % годовых) с тем, чтобы через 5 лет накопленные деньги использовать для инвестирования. Какая сумма окажется на банковском счету предприятия?

Задача 5. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 7 лет с годовым платежом 800, и другая — 3 года и платежом 1500. Годовая ставка процента 11%.

ариант 6

Вопрос 1. Понятие непрерывных процентов.

Вопрос 2. Как определяется наращенная сумма годовой ренты, p-срочной ренты?

Вопрос 3. Параметры финансовых рент.

Вопрос 4. Консолидирование задолженностей.

Задача 1. 10 марта в банк положили сумму 10000 до востребования под ставку 9% годовых сложных процентов. Какую сумму снимет вкладчик 1 ноября?

Задача 2. Проведя усовершенствование технологического процесса предприятие в течение трех последующих лет планирует получение ежегодное увеличение денежного дохода на 50000. Эти деньги оно собирается немедленно вкладывать под 11% годовых, желая через три года накопить сумму для приобретения нового оборудования. Какую сумму денег предприятие получит через три года?

Задача 3.Каждые полгода на банковский счет писателя издательство перечисляет 5000 руб., на которые банк начисляет каждые полгода 5% по схеме сложных процентов. Сколько будет на счете через 3 года?

Задача 4.Предприятие приобрело облигации муниципального займа, которые приносят ему доход $10000, и хочет использовать эти деньги для развития собственного производства. Предприятие оценивает прибыльность инвестирования (получаемых каждый год $10000) в 14 %. Необходимо определить настоящее значение этого денежного потока.

Задача 5. Замените годовую ренту с годовым платежом $600 и длительностью 10 лет семилетней годовой рентой. Ставка процента 8% в год.

Рекомендация. Из уравнения 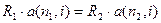находим платеж .

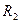ариант 7

Вопрос 1. Понятие ставки процента. Сложные проценты.

Вопрос 2. Простые виды конверсий.

Вопрос 3. Параметры финансовых рент.

Вопрос 4. Параметры финансовых рент.

Задача 1. У Вас есть возможность вложить денежные средства в проект стоимостью 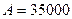. Через год будет возвращено 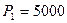, через два года - 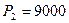, через три года - , через четыре года 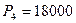. Альтернативный вариант - положить деньги в банк под 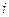процентов годовых. При какой годовой процентной ставке выгоднее вложить деньги в инвестиционный проект?

Задача 2. Предположим, что Вы заключили депозитный контракт на сумму $1000 на 3 года при 9 процентной ставке. Если проценты начисляются ежегодно, какую сумму Вы получите по окончании контракта?

Задача 3. Каждые полгода на банковский счет писателя издательство перечисляет 10000 руб., на которые банк начисляет каждые полгода 7% по схеме сложных процентов. Сколько будет на счете через 2 года?

Задача 4.Для ренты с параметрами: годовая ставка процента – 14%, годовой платеж – 600 д.е., длительность ренты – 4 лет, получить следующие ее характеристики: коэффициенты приведения и наращения; современную и наращенную величины.

Задача 5. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 8 лет с годовым платежом 500, и другая — 4 года и платежом 1700. Годовая ставка процента 7%.

ариант 8

Вопрос 1. Множитель наращения. Соотношение множителей наращения по простым и сложным процентам.

Вопрос 2. Мультиплицирующие и дисконтирующие множители.

Вопрос 3. Сложные конверсии.

Вопрос 4 Параметры ренты. Определение срока ренты.

Задача 1. При какой ставке сложных процентов за 9 лет сумма удваивается?

Задача 2. Банк предлагает 15% годовых. Чему должен быть равен изначальный вклад, чтобы через 3 года иметь на счете 5 млн. руб

Задача 3. Анализируются два варианта накопления средств по схеме аннуитета (поступление денежных средств осуществляется в конце соответствующего временного интервала):

План 1: вносится вклад на депозит $500 каждые полгода при условии, что банк начисляет 8% годовых с полугодовым начислением процентов.

План 2: делается ежегодный вклад в размере $1000 на условиях 9% годовых при ежегодном начислении процентов.

Определите:

а) какая сумма будет на счете через 10 лет при реализации каждого плана? Какой план более предпочтителен?

б) изменится ли ваш выбор, если процентная ставка в плане 2 будет снижена до 8,5%?

Задача 4. Стоит ли покупать за $5500 ценную бумагу, генерирующую ежегодный доход в размере $1000 в течение 7 лет, если коэффициент дисконтирования равен 8%?

Задача 5. Провести детальный анализ ренты длительностью 4 года, годовым платежом R = 1000 д.е. и переменной процентной ставкой: 5% во 2-м году, 8% — в 3-м, 10% — в 4-м году. Определить современную величину данной ренты?

ариант 9

Вопрос 1. Дисконтирование на основе непрерывных процентных ставок. Переменная сила роста.

Вопрос 2. Наращенная сумма p-срочной ренты.

Вопрос 3. Понятие непрерывных процентов.

Вопрос 4 Принцип финансовой эквивалентности обязательств.

Задача 1. Вы имеете 10 млн. рублей и хотели бы удвоить эту сумму через 5 лет. Каково минимально приемлемое значение процентной ставки?

Задача 2. Банк предлагает 12% годовых, чему должен быть равен изначальный вклад, чтобы через 3 года иметь на счете 100 000 руб.

Задача 3. В банк помещен депозит в размере 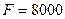руб. По этому депозиту в первом году и втором году будет начислено 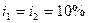, в третьем - , в четвертом 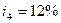и пятом - 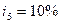. Сколько надо было бы поместить на счет при постоянной процентной ставке 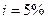, чтобы обеспечить ту же сумму.

Задача 4. Провести детальный анализ ренты длительностью 4 года, годовым платежом R = 1000 д.е. и переменной процентной ставкой: 5% во 2-м году, 8% — в 3-м, 10% — в 4-м году. Определить современную величину данной ренты?

Задача 5. Замените годовую ренту с годовым платежом $700 и длительностью 5 лет трехлетней годовой рентой. Ставка процента 8% в год.

Рекомендация. Из уравнения 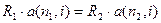находим платеж .

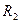ариант 10

Вопрос 1. Понятие номинальной ставки.

Вопрос 2. Принцип неравноценности денег.

Вопрос 3. Какие задачи необходимо решить при объединении рент?

Вопрос 4. Как вычисляется современная величина дискретной ренты при непрерывном начислении процентов.

Задача 1. Банк предлагает 11% годовых. Чему должен быть равен изначальный вклад, чтобы через 2 года иметь на счете 5 млн. руб.

Задача 2 В банк помещен депозит в размере 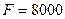руб. По этому депозиту в первом году и втором году будет начислено 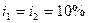, в третьем - , в четвертом 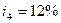и пятом - 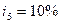. Сколько надо было бы поместить на счет при постоянной процентной ставке 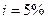, чтобы обеспечить ту же сумму.

Задача 3. Для ренты с параметрами: годовая ставка процента – 12%, годовой платеж – 1000 д.е., длительность ренты – 7 лет, получить следующие ее характеристики: коэффициенты приведения и наращения; современную и наращенную величины.

Задача 4.Предприятие располагает 120,000 и предполагает вложить их в собственное производство, получая в течение пяти последующих лет ежегодно 50,000. В то же время предприятие может купить на эту сумму акции одной солидной корпорации, приносящие 12 процентов годовых. Какой вариант Вам представляется более приемлемым, если считать что более выгодной возможностью вложения денег (чем под 12 процентов годовых) предприятие не располагает?

Задача 5. Замените годовую десятилетнюю ренту с годовым платежом $1000 на ренту с полугодовым платежом по $800. Годовая ставка процента 8%.

Рекомендация. Из уравнения 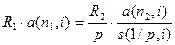находим срок 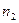.Здесь .

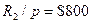ариант 11

Вопрос 1. Каким образом учитывается инфляция при вычислении наращенной суммы?

Вопрос 2. Как определяется эффективная ставка?

Вопрос 3. Дисконтирование по простым процентам.

Вопрос 4 Понятие ставки процента. Сложные проценты. Непрерывные проценты.

Задача 1. Какую ставку должен назначить банк, чтобы при годовой инфляции 12% реальная ставка оказалась равной 6%?

Задача 2 Рассчитайте наращенную сумму с исходной суммы в 2 млн. руб. при размещении ее в банке на условиях начисления сложных процентов, если годовая ставка 15%, а периоды наращения 90 дн., 180 дн., 1 год, 5 лет, 10 лет.

Задача 3. Для ренты с параметрами: годовая ставка процента – 17%, годовой платеж – 1600., длительность ренты – 6 лет, получить следующие ее характеристики: коэффициенты приведения и наращения; современную и наращенную величины.

Задача 4. редприятие располагает $60,000 и предполагает вложить их в собственное производство, получая в течение четырех последующих лет ежегодно $20,000. В то же время предприятие может купить на эту сумму акции одной солидной корпорации, приносящие 18 процентов годовых. Какой вариант Вам представляется более приемлемым?

Задача 5. Замените годовую ренту с годовым платежом 21 000 и длительностью 5 лет семилетней годовой рентой. Ставка процента 9% в год.

Рекомендация. Из уравнения 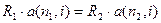находим платеж .

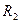ариант 12

Вопрос 1. Консолидирование задолженностей.

Вопрос 2. Капитализированная сумма платежей.

Вопрос 3. Понятие непрерывных процентов.

Вопрос 4 Множитель наращения. Соотношение множителей наращения по простым и сложным процентам.

Задача 1. Рассчитайте наращенную сумму с исходной суммы в 2 млн. руб. при размещении ее в банке на условиях начисления сложных процентов, если годовая ставка 15%, а периоды наращения 90 дн., 180 дн., 1 год, 5 лет, 10 лет.

Задача 2. В банк помещен депозит в размере 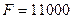руб. По этому депозиту в первом году будет начислено 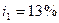, во втором году 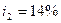в третьем - 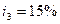, в четвертом 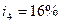и пятом - 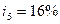. Сколько надо было бы поместить на счет при постоянной процентной ставке 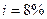, чтобы обеспечить ту же сумму.

Задача 3. Дана вечная рента с годовым платежом 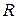при ставке процента 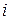. Известно, что ее современная величина, т.е. в момент 0, равна 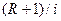. Найдите ее величину в произвольный момент 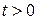. При каком 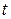эта величина максимальна, минимальна?

Задача 4. Провести детальный анализ ренты длительностью 4 года, годовым платежом 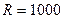д.е. и переменной процентной ставкой: 9% во 2-м году, 11% — в 3-м, 12% — в 4-м году. Определить современную величину этой ренты?

Задача 5. Замените годовую ренту с годовым платежом 1200 и длительностью 5 лет четырехлетней годовой рентой. Ставка процента 8% в год.

Рекомендация. Из уравнения 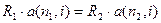находим платеж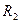

ариант 13

Вопрос 1. Поток платежей. Основные характеристики.

Вопрос 2. Дисконтирование на основе непрерывных процентных ставок. Переменная сила роста.

Вопрос 3. Определение процентных ставок для сложных процентов.

Вопрос 4 Понятие номинальной ставки.

Задача 1. Какую ставку должен назначить банк, чтобы при годовой инфляции 14% реальная ставка оказалась равной 7%?

Задача 2. Рассчитайте будущую стоимость $1000 для следующих ситуаций:

· 5 лет, 8% годовых, ежегодное начисление процентов;

· 5 лет, 8% годовых, полугодовое начисление процентов;

· 5 лет, 8% годовых, ежеквартальное начисление процентов.

Задача 3. Для ренты с параметрами: годовая ставка процента – 7%, годовой платеж – 10000., длительность ренты – 5 лет, получить следующие ее характеристики: коэффициенты приведения и наращения; современную и наращенную величины.

Задача 4. Определить процентную ставку для 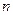- летнего займа в 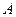рублей с ежегодной выплатой в 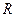рублей. Решить задачу для следующих исходных данных:

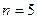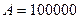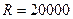лет, руб., руб.

Задача 5. Найдите ренту, которая представляет собой сумму для двух годовых рент: одна длительностью 7 лет с годовым платежом 1300, и другая — 4 года и платежом 17 000. Годовая ставка процента 9%.

ариант 14

Вопрос 1. Классификация экономико-математических моделей.

Вопрос 2. Какие задачи необходимо решить при объединении рент.

Вопрос 3. Современная величина дискретной ренты при непрерывном начислении процентов

Вопрос 4. Соотношение между наращенной и современной величинами ренты.

Задача 1. Рассчитайте текущую стоимость каждого из приведенных ниже денежных поступлений, если коэффициент дисконтирования равен 12%:

а) 5000 руб., получаемые через 3 года;

б) 50000. руб., получаемые через 10 лет.

Задача 2. В банк помещен депозит в размере 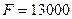руб. По этому депозиту в первом году будет начислено 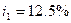, во втором году 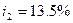в третьем - 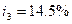, в четвертом 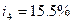и пятом - 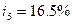. Сколько надо было бы поместить на счет при постоянной процентной ставке 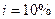, чтобы обеспечить ту же сумму.

Задача 3. Предприятие рассматривает два альтернативных проекта капитальных вложений приводящих к одинаковому суммарному результату в отношении будущих денежных доходов:

Год	Проект 1	Проект 2
	$30,000	$6,000
	$40,000	$40,000
	$20,000	$30,000
	$6,000	$20,000
Всего	$	$

Оба проекта имеет одинаковый объем инвестиций. Предприятие планирует инвестировать полученные денежные доходы под 18% годовых. Сравните современные значения полученных денежных доходов.

Задача 4. Рассмотрим годовую ренту при n = 8, i= 12%. Что бо­лее увеличит наращенную величину ренты: увеличение длительности на 1 год или увеличение процентной ставки на 1%?

Задача 5. Замените годовую ренту с годовым платежом 2700 и длительностью 7 лет пятилетней годовой рентой. Ставка процента 8% в год.

Рекомендация. Из уравнения 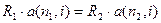находим платеж .

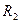ариант 15

Вопрос 1. Что означает термин «упущенная выгода»?

Вопрос 2. Понятие ставки процента. Сложные проценты.

Вопрос 3. Простые виды конверсий.

Вопрос 4 Дайте определение понятию «финансовая рента».Параметры финансовых рент.

Задача 1. По договору зафиксирован платеж через 3 года в размере 1000д.е. Через год процентная ставка увеличилась. Кому это выгодно: тому, кому будут платить, или тому, кто будет платить?

Задача 2. Что более предпочтительно - получить $2000 сегодня или $5000 через 8 лет, если коэффициент дисконтирования равен 8%?

Задача 3. Приведены данные о денежных потоках:

Поток	Год
А
В				-

Рассчитайте для каждого потока показатели NPV при r = 12% для двух случаев: а) потоки имеют место в начале года; б) потоки имеют место в конце года.