Среднеквадратичное отклонение

Билет 1

1. На практике, некоторая местность имеет неопределенное количество точек на плоскости. Первоначально мы не знаем точных значений этих точек относительно заранее известных, будь это высотные отметки, координаты, содержание руды и др. В данном случае, точки которые мы измеряем считаются случайными величинами.

Случайные величины – величины, которые в результате опытов могут занять те или иные заранее неизвестные значения. Различают дискретные и непрерывные случайные величины.

Непрерывные величины – задается функцией распределения и плотностью вероятности (графически – их кривыми)

Дискретные величины – задаются рядом распределения (графически – полигоном распределения или гистограммой) и функцией распределения.

Пусть дискретная величина Xв результате опыта может получать различные значения xi с вероятностью pi(Spi = 1).

Связь между возможными величинами и вероятностями их появления устанавливает закон распределения. Простейшая форма задания такого закона – ряд распределения (таблица значений xibpi)

Графически ряд распределения изображается полигоном распределения: по горизонтальной оси располагают случайные величины, по вертикальной – вероятности этих значений.

2. Форма залежи полезного ископаемого в недрах определяется поверхностями раздела полезного ископаемого от вмещающих его боковых горных пород. Эти поверхности изображают на топографических планах изогипсами или горизонталями. Геометрические графики называют гипсометрическими планами или структурными планами (картами).

построение гипсометрических планов производят по данным разведки непосредственным и косвенным способами. Месторождения платформенного типа со слабо наклонным или почти горизонтальным залеганием обычно разведывают сетью вертикальных разведочных скважин располагаемых более менее равномерно по площади участка (в ряде случаев по геометрической сетке). По данным разведочных скважин – абсолютным или относительным отметкам почвы и кровли залежи - строят гипсометрические планы. Изолинии строят по методу многогранника или с использованием инвариантных линий.

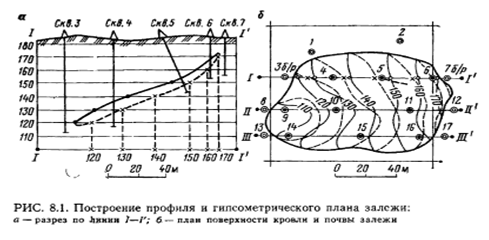Гипсометрический план месторождений с наклонным и крутым залеганием строится непосредственно по данным разведочных скважин или косвенно по разведочным линиям, которые обычно располагают вкрест простирания.

3. Мода – Модой +случайной дискретной величины называется ее наиболеевероятное, наиболее часто встречающееся значение. Длянепрерывной величины модой является ее значение, в которомплотность вероятности максимальна. Мода и математическоеожидание случайной величины в общем случае не совпадают.Они совпадают лишь при симметричном распределении. Распределение называется полимодальным когда кривая имеет не один а два или более максимумов.

для дискретного несгруппированного вариационного ряда модальным является тот вариант, который характеризуется наибольшей частотой.

Медиана случайной величины – значение для которого одинаково вероятно окажется ли случайная величина меньше или больше медианы, т.е., это срединная величина упорядоченного вариационного ряда. Геометрически на графике медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

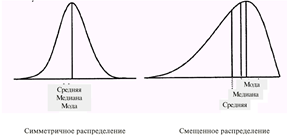
При симметричном распределении, положение моды и медианы совпадает. Медиана важна для анализа ассиметричных графиков.

Билет 2

1. Геометризация месторождения – это процесс его изучения и познания. Процесс этот постепенный и последовательный. Каждые вновь получаемые данные при разведке и разработке месторождения уточняют прежние представления о нем, позволяют корректировать ранее составленные графики и использовать их для принятия правильного решения задач последующей разведки и разработки. Геометризация не исключает геологического изучения, являясь научной математической (геометрической) базой комплексного изучения недр.

В процессе геометризации осуществляются новые теоретические разработки в области математических методов обработки информации. При этом решается две основные задачи:

- на основе использования всей полученной о месторождении на данном этапе информации создать наиболее правдоподобную модель месторождения с оценкой ее точности (установить степень соответствия модели в натуре).

- установить минимальное число точек наблюдений (скважин, проб, и т. п.) и их расположение при разведке, по данным которых построенная модель месторождения будет представлять натуру с погрешностью не превышающей величины, устанавливаемой требованиями горного производства.

2.

Гипсометрический план может строится напрямую по отметкам скважин или косвенно по разведочным линиям.

На листе бумаги наносят координатную сетку, разведочные линии, все разведочные скважины с отметками поверхностей напластования и мощности залежи, линию выхода залежи на поверхность или под наносы, границу или контур залежи в недрах. Контур залежи в недрах проводят посередине между безрудными и рудными скважинами или по изолинии нулевой мощности залежи. В ряде случаев нулевой контур вначале определяют на профилях или вертикальных разрезах по разведочным линиям, а затем переносят на план (рис.).

На геологических разрезах или профилях точки пересечения линий высотной сетки с профилем поверхности залежи проектируют на одну из линий сетки и подписывают соответствующие отметки. С разрезов эти точки переносят на план по соответствующим разведочным линиям.

Соединяя точки с одинаковыми отметками плавными кривыми, проводят горизонтали поверхности залежи, при этом учитывают характер залегания залежи по геологическому плану (карте). Сплошные изолинии изобр. поверхность кровли, пунктирными – поверхность почвы земли. На контурной линии изолинии поверхности кровли переходят в одноименные изолинии поверхности почвы залежи. Контур, составленный изолиниями кровли и почвы с одинаковой отметкой, представляет на плане горизонтальное сечение залежи на данном горизонте. Горизонтали залежи проводят с учетом разведочных выработок.

3.

Билет 3

1.

Асимметрия характеризует надежность выполнения первого свойства случайных ошибок – равновероятности одинаковых по величине положительных и отрицательных ошибок. При А = 0 ряд симметричен. При А>0 положительные ошибки встечаютсячаще чем равные им отрицательные.

2. Форма залежи полезного ископаемого в недрах определяется поверхностями раздела полезного ископаемого от вмещающих его боковых горных пород. Эти поверхности изображают на топографических планах изогипсами или горизонталями. Геометрические графики называют гипсометрическими планами или структурными планами (картами).

построение гипсометрических планов производят по данным разведки непосредственным и косвенным способами. Месторождения платформенного типа со слабо наклонным или почти горизонтальным залеганием обычно разведывают сетью вертикальных разведочных скважин располагаемых более менее равномерно по площади участка (в ряде случаев по геометрической сетке). По данным разведочных скважин – абсолютным или относительным отметкам почвы и кровли залежи - строят гипсометрические планы. Изолинии строят по методу многогранника или с использованием инвариантных линий.

Гипсометрический план месторождений с наклонным и крутым залеганием строится непосредственно по данным разведочных скважин или косвенно по разведочным линиям, которые обычно располагают вкрест простирания.

3.

Класс m, м	Частота	Частость p'	Накопл. Частость p
Пометки	n
0~2			0,0833	0,0833
2~4			0,1417	0,225
4~6			0,1916	0,4166
6~8			0,2667	0,6833
8~10			0,1667	0,85
10~12			0,0833	0,9333
12~14			0,0583	0,9916
14~16			0,0083	0,9999
			0,9999

(пример. Рекоммендую придумать свои данные. Пометки помечают точками и линиями в виде конвертика количество значений n. Например, n=10 показывается как 4 точки и 6 линий между точками. Является устаревшим методом ведения счета при подсчете кол-ва n)

Билет 4

1. Виды геометризации недр. Геологические показатели разделяются

на признаки, характеризующие форму массива горных

пород, его свойства и процессы, происходящие в недрах.

В зависимости от того, какую сторону недр главным образом

изучают, различают следующие виды геометризации:

форму залежей полезных ископаемых и условий их залегания;

размещения физико-химических и технологических свойств залежей

и вмещающих пород; процессов, происходивших и происходящих

в недрах — как изменение формы и свойств вещества

в пространстве и во времени.

При геометризации каждого вида составляют комплекс

горно-геометрических чертежей.

Форму залежей и условия их залегания представляют гипсометрические

планы кровли и почвы залежи, изолинии мощности,

изоглубины залегания, изогипсы поверхности водоупорного

горизонта, поверхностей тектонических нарушений и пр.

Размещение свойств залежей и массива горных пород представляют

графики изолиний содержания того или иного компонента

в полезном ископаемом, изолинии трещиноватости, пористости,

крепости того или иного слоя горных пород и др.

Процессы, происходящие в недрах, такие как изменение режима

подземных вод, геотемпературного поля Земли, напряженного

состояния массива горных пород из-за проведения в нем горных выработок и другие, при геометризации представляются

соответствующими графиками в виде изолиний или

векторов, характеризующих направления и скорости изучаемых

параметров.

Чертежи при геометризации форм, свойств и процессов

должны быть построены с учетом всей полученной информации.

Они должны максимально правдоподобно отражать

недра на данном этапе их изучения, так как являются основой

для решения комплекса вопросов рациональной разведки и

разработки месторождений.

В зависимости от этапа изучения месторождения, конкретных

задач и масштабов составления горно-геометрических чертежей

различают региональную, детально-разведочную и эксплуатационную

геометризацию месторождений.

Р е г и о н а л ь н а я г е оме т ри з а ци я осуществляется

в мелких масштабах (1 :5 0 0 0 0—1:500000) по данным поисковых

работ, космической, аэрофотографической, геологической и

геофизической съемки. Она позволяет делать широкие обобщения

и общие прогнозы, определять районы, перспективные для

дальнейшей разведки месторождений.

Д е т а л ь н о - р а з в е д о ч н а я г еом р т р и з а ц и я осуществляется

в масштабах от 1:5000 до 1 : 50000 на основе данных

детальной разведки, геологической структурно-геологической

и геофизической съемок. На этой стадии составляют различные

горно-геометрические графики формы, условий залегания

залежи, размещения в них компонентов и пр. По материалам

геометризации оценивают месторождения, подсчитывают запасы,

проектируют горные предприятия.

Эк с п л у а т а ц и о н ную г е о м е т р и з а ц ию составляют

в масштабах 1 100—1 :5000. Ее проводят на основе материалов

детальной разведки и богатой горно-геологической информации,

получаемой при проходке подготовительных и очистных горных

выработок.

Эксплуатационная геометризация позволяет вскрывать закономерности

структурного и качественного характера, на основе

которых становится возможным строить прогнозы на ближайшие

участки недр и планировать рациональную их разработку.

Горно-геометрические графики при геометризации строят

в проекции на горизонтальную, наклонную и вертикальную плоскости.

Выбор плоскости проекции определяется углом падения

залежи и назначением графика. Чаще всего их строят в проекции

на горизонтальную плоскость и называют планами.

Региональная, детально-разведочная и эксплуатационная

геометризация представляют собой этапы последовательного

изучения и познания месторождения, начиная от его обнаружения

и до полной отработки.

2.

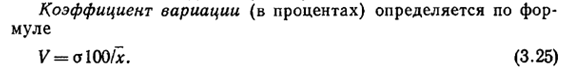
3. Глубина залегания залежи — расстояние по вертикали от земной

поверхности до кровли залежи.

В разных точках земной поверхности полезное ископаемое

залегает на разных глубинах. Геометрическое место точек на

земной поверхности с одинаковыми значениями в них глубин

называют изоглубиной. Изоглубины залегания есть не что

иное, как изомощности покрывающей залежь толщи пород. Поэтому

определения и способы построения изоглубин аналогичны

построениям изомощностей.

При косвенном способе изоглубины строят, вычитая из

плана поверхности рельефа план поверхности кровли залежи.

Практически график изоглубин дает возможность быстро

прочитать по изолиниям глубину залегания в любой точке

земной поверхности. Изоглубина с определенной отметкой может

быть границей открытых разработок.

По изоглубинам, как по изомощностям вскрыши (покрывающей

толщи пород), определяют с помощью объемной палетки

Соболевского объемы вскрышных работ при открытых

разработках.

Изоглубины строят для определения коэффициентов

вскрыши путем деления изоглубин залегания на изомощности

залежи.

Изоглубина с отметкой нуль есть линия ____выхода висячего

бока залежи на земную поверхность.

На плане линия выхода определяется как линия пересечения

одноименных горизонталей земной поверхности и висячего

бока залежи.

Если на данном участке месторождения имеются наносы

с определенной средней глубиной, то изоглубина залегания полезного ископаемого с отметкой, равной средней глубине наносов,

есть линия выхода висячего бока залежи под наносы.

Знать эту линию необходимо при задании разведочных шурфов

или скважин для уточнения выхода залежи под наносы.

Билет 5

1. Роль математической статистики в геометризации месторождения заключается в систематизации, обработке и обобщении числовой информации полученной в результате разведки и отработки, выполнении расчетов для построения горно-геометрических графиков и моделей, с помощью которых мы получаем возможность визуального анализа и выявления отдельных ошибок измерений и графических построений. По сути, геометризация основана на математической статистике.

2. Мощность залежи полезного ископаемого в различных точках

часто различна, поэтому при определении мощности ее значение

относят к определенным точкам — к точкам висячего бока

залежи.

Изменения мощности полезного ископаемого, вмещающих

его боковых пород, водоносных или водоупорных горизонтов,

а также изменения мощности отдельных свит или пачек, слоев

горных пород между соседними залежами — отображаются

в изолиниях мощности.

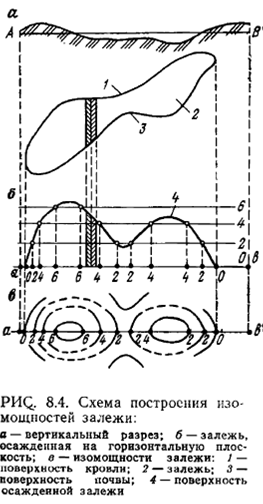
Изомощность— геометрическое место точек с одинаковыми

значениями мощности по нормали к плоскости проекции (см.

гл. 5).

Система изомощностей на плоскости проекции представляет

изображение поверхности топографического порядка.

Эта поверхность реально в природе не существует. Геометрически

она представляет поверхность, которая образуется,

если мысленно всю массу полезного ископаемого разделить на

элементарные столбики и осадить их на плоскость проекции

(рис. 8.4).

Если поверхность осажденной залежи рассечь горизонтальными

плоскостями, отстоящими на одинаковом расстоянии друг

от друга, и линии пересечения спроектировать на горизонтальную

плоскость О—О, то получаемые при этом горизонтали поверхности

тождественны изолиниям равной мощности залежи.

Изомощности залежи строят непосредственным и косвенными

способами.

Непосредственный способ состоит в построении изолиний по

отметкам равной мощности на плане. При геометрическом анализе

отметок необходимо учитывать наличие зон раздува, размыва,

пережима — зон с измененной мощностью, имеющими,

как правило, резкие границы. Поэтому нельзя производить интерполяцию

между скважинами, попавшими в эту зону. Зоны

следует предварительно оконтуривать.

Построение изомощностей начинают с участков, вскрытых

горными выработками или наиболее изученных.

В проекциях на вертикальную плоскость изолинии мощности

строят аналогичным образом.

Косвенный способ построения изолиний мощности имеет две

разновидности:

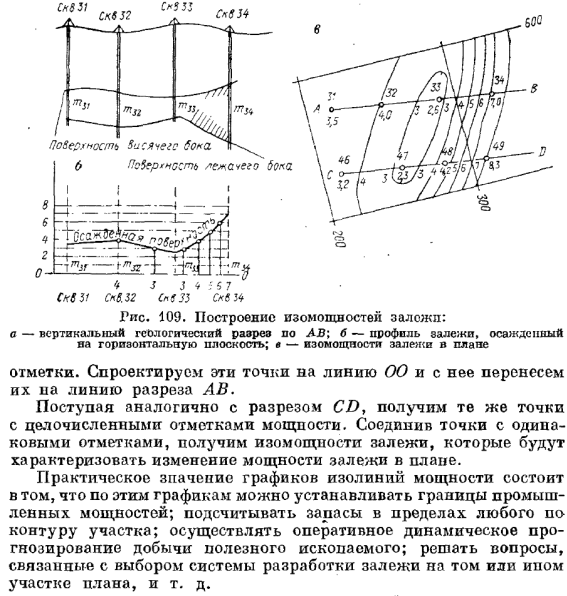
1) с использованием геологических разрезов или профильных

сечений залежи. На плане отмечают линии разрезов. С помощью

раствора циркуля или линейки последовательно устанавливают

отрезки по величине кратные выбранному сечению.

На разрезах находят точки с равной мощностью-залежи по

нормали к плоскости проекции. Точки вначале проектируют на

горизонтальную линию разреза, а затем переносят на план и подписывают соответствующие

целочисленные отметки. Соединяя

точки с одинаковыми отметками

плавными кривыми, получают

изомощности залежи.

2) путем графического вычитания

из поверхности висячего

бока залежи поверхность

лежачего бока. Этот способ является

единственным при построении

изомощностей, когда залежь

сложной формы разведана

сочетанием вертикальных, наклонных

и искривленных скважин,

когда по скважинам трудно

определить нормальную

к плоскости проекции мощность.

В этом случае по данным бурения

проще построить гипсометрические

планы висячего и лежачего

боков залежи и через них

построить изомощности.

Этот способ является также

единственным при увязке по информации

ряда взаимосвязанных

показателей залежи.

3. Статистические средние значения часто находят параллельно

с определением корреляции (соотношения или соответствия),

т. е. некоторых вероятностных связей между двумя или несколькими

показателями месторождения. Для многих месторождений обнаружены зависимости изменения одного геологическогопризнака от изменения другого, например зависимость содержания

компонента от мощности залежи или плотности руды

и т. п.

Пусть имеем несколько пар значений (хі, Уі )двух случайных

величин X и У. Выберем плоскую прямоугольную систему

координат. В этой системе за ось абсцисс примем ось случайной

величины X, которую в дальнейшем будем считать факториальной,

за ось ординат примем ось случайной величины У, которую

будем считать функциональной. Обозначим каждую пару

значений (хі, уі) случайных величин точкой в выбранной системе

координат, откладывая на соответствующих осях значения

Хіи уі. Совокупность полученных точек даст поле корреляции

диализируемых случайных величин (рис. 3.2).

Форма поля корреляции позволяет произвести качественную

оценку наличия и тесноты связи между случайными величинами.

Проведем осевую линию AB поля корреляции. Если

AB — прямая, параллельная одной из осей координат (например,

оси X), то между величинами связи нет: при увеличении

значений одной из них (X) значения второй (У) в среднем не

меняются. Если AB — наклонная прямая, то между величинами

имеется прямолинейная связь; если AB — кривая, то между

величинами существует связь, выражающаяся уравнением более

высокого порядка.

Разброс (удаленность) точек от осевой линии AB поля корреляции

характеризует тесноту связи. Чем ближе точки расположены

к осевой линии, тем теснее связь, и наоборот.Детальная количественная оценка наличия и тесноты корреляции

между двумя (парная корреляция) и более (множественная

корреляция) признаками производится на основе статистического

расчета, именуемого корреляционным анализом.

Билет 6

1. Форма залежи определяется серией горизонтальных или вертикальных,

а иногда и тех и других взаимно увязанных разрезов,

выполненных в определенном масштабе. Для наглядности

их строят в векторной или иной проекции.

2.

Асимметрия характеризует надежность выполнения первого свойства случайных ошибок – равновероятности одинаковых по величине положительных и отрицательных ошибок. При А = 0 ряд симметричен. При А>0 положительные ошибки встечаютсячаще чем равные им отрицательные.

3. Геологические разрезы составляют по каждой разведочной

линии. Построение Вертикального разреза начинают с нанесения

высотной сетки -системы горизонтальных параллельных

линий, профиля рельефа земной поверхности по данному сечению

и выходов полезного ископаемого и маркирующих горизонтов.

Затем наносят устья и оси горных и разведочных

выработок, находящихся в плоскости 'общего разреза. По осям

разведочных выработок последовательно наносят в масштабе

но Точкам встреченные горные породы, полезные ископаемые,

тектонические--рдзрывы с учетом углов падения и выдержанности нормальных расстояний между ними. После этого соответственные

точки, принадлежащие одной залежи, соединяют.

При этом построение Начинают со слоя, имеющего наибольшее

число фактических данных. Изображение горных пород на разрезе

оформляют в красках или условных знаках по стандарту.

Масштаб разрезов принимают равным масштабу геологической

или структурной карты. Вертикальный и горизонтальный

масштабы обычно берут одинаковыми. Однако в некоторых

случаях для выделения на разрезе литологических разновидностей

вертикальный масштаб принимают в несколько раз

крупнее горизонтального. В этом случае на разрезе искажаются

углы падения залежи и слоев горных пород.

Горизонтальные разрезы обычно строят на уровне отметок

подземных горных выработок. Данные для их построения получают

при проведении горизонтальных горных выработок или

по ряду вертикальных разрезов.

При построении разрезов свиты пластов по данным разведочных

скважин или квершлажных горных выработок требуется

иногда строить разрезы по разным направлениям.

Так, например, по вертикальному геологическому разрезу

квершлага требуется составить разрез по нормали и напластованию

слоев свиты с углом падения б. Для этого из некоторой

точки Она оси квершлага О А под углом 90 — б к ней

проводя линию OB. Далее на эту линию проектируют значения

мощности слоев с линии ОА перпендикулярно к линии

OB. Обозначив слои в условных знаках, получают графически

нормальный разрез свиты пластов.

Аналогично поступают при построении разреза по линии

ОС — горизонтальной линии, составляющей некоторый угол Q

с осью квершлага. Значения мощности слоев в этом случае

с линии ОА на линию ОС проектируют перпендикулярно

к ОА.

Геологические разрезы, гипсометрические планы и геологическая

карта составляются одновременно и взаимно увязываются

как по координатам X, У, Z, так и по элементам изображаемого

объекта.

Билет 7

1.Элементы залежи и их практические значение.

2. Построение плана изомощности.

3. Числовые характеристики случайных величин.

Числовыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин

Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:

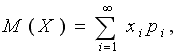
Свойство 1. Мат. ожидание постоянной равно этой постоянной.

Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий:

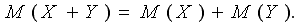
Из этого свойства следует следствие:

Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий:

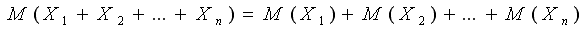
Свойство 3. Математическое ожидание произведения независимых случайных величин Х и Y равно произведению математических ожиданий этих вел. M(XY)=M(X)·(M)Y.

Следствие. Постоянный множитель можно вынести за знак математических ожидания: М(сХ) = сМ(Х)

Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:

D[Х]=M[X-M(X)]²

Свойство 1. Дисперсия постоянной величины равна нулю.

Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:

D(cX) = c²D(X)

Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий:

D(X+Y) = D(X) + D(Y), от сюда следствие:

если х₁, х₂,..., х_n - случайные величины, каждая из которых независима от суммы остальных, то

D(X₁+X₂+...+X_n) = D(X₁) + D(X₂)+...+D(X_n).

Моментом k-порядка называется математическое ожидание k-й степени отклонения случайной величины Х от некоторой постоянной с.

Если в качестве с берется нуль, моменты называются начальными

ν_k = М(Х)^k

Если с = М(Х), то моменты называются центральными

μ = M[X – M(X)]^k

Билет 8

1. Значение структурных показателй залежи для научных исследований.

2. Среднеквадратическая ошибка, дисперсия при статической обработке.

Дисперсия

Речь идет о дисперсии случайной величины. Это очень важный показатель, который активно используется в различных методах статистического анализа (проверка гипотез, анализ причинно-следственных связей и др.). Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

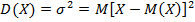
То есть дисперсия - это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое.

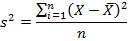
где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Примечание. Для расчета дисперсии в Excel предусмотрена специальная функция.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. В то же время не все так плохо. При увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной. Поэтому при работе с большими размерами выборок можно использовать формулу выше.

Язык знаков полезно перевести на язык слов. Получится, что дисперсия - это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, мы просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Разгадка заключается всего в трех словах.

Однако в чистом виде, как, например, средняя арифметическая, или индекс, дисперсия не используется. Это скорее вспомогательный и промежуточный показатель, который необходим для других видов статистического анализа. У нее даже единицы измерения нормальной нет. Судя по формуле, это квадрат единицы измерения исходных данных. Без бутылки, как говорится, не разберешься.

Среднеквадратичное отклонение

Дабы вернуть дисперсию в реальность, то есть использовать в более приземленных целей, из нее извлекают квадратный корень. Получается так называемое среднеквадратичное отклонение (СКО). Встречаются названия «стандартное отклонение» или «сигма» (от названия греческой буквы). Формула стандартного отклонения имеет вид:

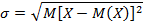
Для получения этого показателя по выборке используют формулу:

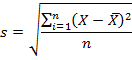
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Среднеквадратичное отклонение, очевидно, также характеризует меру рассеяния данных, но теперь (в отличие от дисперсии) его можно сравнивать с исходными данными, так как единицы измерения у них одинаковые (это явствует из формулы расчета). Но и этот показатель в чистом виде не очень информативен, так как в нем заложено слишком много промежуточных расчетов, которые сбивают с толку (отклонение, в квадрат, сумма, среднее, корень). Тем не менее, со среднеквадратичным отклонением уже можно работать непосредственно, потому что свойства данного показателя хорошо изучены и известны. К примеру, есть такое правило трех сигм, которое гласит, что у нормально распределенных данных 997 значений из 1000 находятся в пределах ±3 сигмы от средней арифметической. Среднеквадратичное отклонение, как мера неопределенности, также участвует во многих статистических расчетах. С ее помощью устанавливают степень точности различных оценок и прогнозов. Если вариация очень большая, то стандартное отклонение тоже получится большим, следовательно, и прогноз будет неточным, что выразится, к примеру, в очень широких доверительных интервалах.

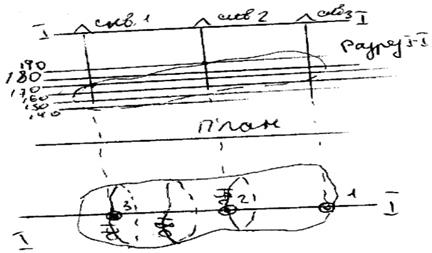
Гипометрический план качественных показателей земли. Методы построения и назначения гипсометрических планов.

Форму залежи ПИ могут определить следы поверхности раздела: поверхности лежачего и висячего боков залежи, тектонических разрывов и слоев залежи с минимальным содержанием компонентов для тех случаев когда ПИ постепенно переходит в безрудные боковые породы.

Планы, с нанесенными на них изогипсами называются гипсометрическими(структурными)Планы могут строиться непосредственным или косвенным способом.

Непосредственный способ применяется дня МПИ с пологим залеганием При построении планов используется метод инварных линий или многогранника При крутом или наклонном залегании метод многогранника или профилей.

При малой разведанности применяются следующие виды построения планов:

1. нормальная мощность пород между пластами имеет постоянную величину,

2. мощность пласта на плане переменная.

Применяется косвенный способ

Гипсометрические планы построенные с учетом данных горных работ и элементов залегания, более точно отображают поверхность залежи, чем планы, построенные по данным разведки. Их используют при прогнозировании показателей залежи и решении текущих задач по разработке соседних участков.

Назначение: используется при прогнозировании показателей залежи и при решении текущих задач по разработке соседних пластов. Гипсометрические планы поверхности почвы и кровли залежи на плане дают полное представление о залежи и широко применяются на практике для решения многих задач по вскрытию и разведке МПИ. Особое значение гипсометрические планы имеют при разработке открытым и дренажным способам. При разработке пластовых МПИ по категории разведанности и изученности: гипсометрию проводят по почве пласта и структурным колонкам залежи. Используются также при планировании горных работ, решении задач рационального размещения объектов и сооружений на ЗП. Служат как материал для изучения тектоники МПИ, определения вида складок и разрывных нарушений. Применяются при решении задач о направлении и длине выработок, составлении прогнозов и распространения нарушений на соседние пласты и нижние горизонты.

Билет 9

1. Метод инвариантных линий при построении гипсометрического плана.

2. План почвы залежи и ее практическое значение.

3.Корреляционный анализ при малом числе наблюдений. При малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по следующей формуле:

Величина коэффициента корреляции изменяется в интервале .

При между двумя переменными существует функциональная связь, при - прямая функциональная связь. Если , то значение Х и У в выборке некоррелированы; в случае, если система случайных величин имеет двумерное нормальное распределение, то величины Х и У будут и независимыми.

Если коэффициент корреляции находится в интервале , то между величинами Х и У существует обратная корреляционная связь. Это находит подтверждение и при визуальном анализе исходной информации. В этом случае отклонение величины У от среднего значения взяты с обратным знаком.

Если каждая пара значений величин Х и У чаще всего одновременно оказывается выше (ниже) соответствующих средних значений, то между величинами существует прямая корреляционная связь и коэффициент корреляции находится в интервале .

Если же отклонение величины Х от среднего значения одинаково часто вызывают отклонения величины У вниз от среднего значения и при этом отклонения оказываются все время различными, то можно предполагать, что значение коэффициента корреляции стремится к нулю.

Следует отметить, что значение коэффициента корреляции не зависит от единиц измерения и выбора начала отсчета. Это означает, что если переменные Х и У уменьшить (увеличить) в К раз либо на одно и то же число С, то коэффициент корреляции не изменится.

Строительство, как немногие отрасли экономики, в силу длительного инвестиционного цикла, немыслимо без планирования. Планирование в строительстве - сложная вещь, т.к. необходимо учитывать многие факторы, такие как :

· Данные проектно-сметной документации;

· Взаимосвязь между подразделениями;

· Использование субподрядных организаций;

· Ограниченность материальных и трудовых ресурсов;

· Своевременность поставки сырья и материалов.

План должен охватывать все стороны деятельности строительной компании:

· Производственную;

· Хозяйственную;

· Финансовую.

Одним из современных методов финансового планирования является бюджетирование. Под бюджетированием понимается управленческая технология финансового планирования, которая позволяет контролировать и анализировать планируемые и получаемые финансовые показатели [3]. Основным инструментом здесь является бюджет. Под бюджетом понимается финансовый план, в котором все показатели относятся либо к доходной, либо к расходной части.

При постановке бюджетирования строительной деятельности необходимо учитывать специфические особенности, присущие данной отрасли экономики.

Для данной сферы функционирования финансов характерна некоторая специфика, обусловленная особенностями складывающихся здесь экономических отношений. Выделим следующие особенности:

1) более продолжительный производственный цикл, обуславливающий повышенную потребность в оборотных средствах;

2) функционирование строительных организаций осуществляется в различных территориально-климатических зонах, что влияет на индивидуальную стоимость сдаваемых объектов, а также на равномерность поступления выручки;

3) сметная стоимость строящихся объектов устанавливается исходя из договоров с заказчиками и поставщиками;

4) этапы осуществляемых строительно-монтажные работ характеризуются различной степенью трудоемкости, материалоемкости, финансовой обеспеченности;

Осуществление строительства происходит, как правило, в несколько этапов: 1) геологоразведовательных работ; 2) разработки сметы строительства; 3) осуществление строительных и монтажных работ. Финансирование проводимых работ осуществляется заказчиками, а работы выполняются специализированными организациями. Подобная детализация обуславливает выделение в данной сфере финансовых отношений следующих компонентов, также характеризующихся своими особенностями:

- финансы заказчика;

- финансы проектных организаций;

- финансы геологоразведовательных организаций;

- финансы строительной организации.

Различают подрядный и хозяйственный способы ведения работ.

При подрядном способе строительная организация привлекает для отдельных видов работ специализированные организации (подрядчики), которые в свою очередь также могут иметь заключенные договора со специализированными исполнителями (субподрядчики).

При хозяйственном способе строительства организация осуществляет все виды работ собственными силами.

Планирование себестоимости работ осуществляется строительной организацией самостоятельно при разработке финансовых планов на основе заключенных договоров. Себестоимость строительных работ может включать элементы:

- затраты непосредственно связанные с осуществлением строительных работ;

- затраты связанные с обслуживанием произодственного процесса;

- затраты некапитального характера, обусловленные совершенствованием технологии строительства, улучшением отдельных видов работ и т.д.

- текущие затраты: на эксплуатацию очистных сооружений, природоохранные мероприятия и др.;

- дополнительные затраты (например, на осуществление работ вахтовым способом);

- другие виды затрат.

Финансовый результат (прибыль или убыток) деятельности строительной организации слагается из финансового результата от сдачи заказчику объектов, работ и услуг, предусмотренных договорами, реализации на сторону основных средств, иного имущества организации, продукции и услуг подсобных и вспомогательных производств, находящихся на балансе строительной организации, а также доходов от внереализационных операций, уменьшенных на сумму расходов по ним.

Балансовая прибыль может быть рассчитана по формуле:

Пб = Прп + Фри + Дв – Рв

где Пб - прибыль (убыток) балансовая;

Фри - финансовый результат от реализации основных средств и иного имущества;

Дв - доходы по внереализационным операциям;

Рв - расходы по внереализационным операциям.

Прибыль (убыток) от сдачи заказчику строительных объектов, других работ, предусмотренных договором определяется как разница между выручкой от их реализации по ценам установленным в договоре, без налога на добавленную стоимость и других вычетов, предусмотренных законодательством, и затратами на их производство и сдачу.

Учет вышеотмеченных особенностей функционирования финансов строительной сферы, знание особенностей и этапов организации строительных работ, методов их осуществления позволяют в наибольшей степени максимизировать положительный финансовый результат от осуществления данного вида деятельности.

Для характеристики финансовой устойчивости могут быть также использованы коэффициенты:

1. Обеспеченности собственными = собственные оборотные средства

оборотными средствами запасы и затраты

Показывает наличие собственных оборотных средств необходимых для финансовой устойчивости, его нормальное значение К ≥ 0,6-0,8

2.Маневреннооти= собственные оборотные средства

общая величина собственных средств

Показывает какая часть собственных средств находится в мобильной форме позволяющей относительно свободно маневрировать этими средствами. В качестве ориентировочного значения можно назвать 0,5.

3. Автономии = собственные средства / итог баланса

Показывает долю собственных средств в общем объеме ресурсов предприятия. Нормальным значением можно считать К≥0,5 - в этом случае все обязательства предприятия покрываются его собственными средствами.

4.Краткосрочной задолженности = краткосрочные обязательства / общая величина обязательств.

Следует помнить, что внешним проявлением финансовой устойчивости является платежеспособность предприятия т.е. его способность в срок рассчитываться по своим обязательствам. Предприятие считается платежеспособным если имеющиеся у него денежные средства, краткосрочные финансовые вложения (ценные бумаги) и активные расчеты (расчеты с дебиторами) покрывают его краткосрочные обязательства.

Билет 10

1. Качественные показатели залежи и их значение при планировании горных работ.

2. Цель проведения геометризации месторождения

3. Геометризация структурных показателей залежи.