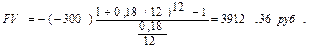Существует три основных вида операций
|
 |
|
|
 | |||||
| |||||
|
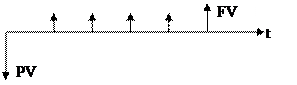
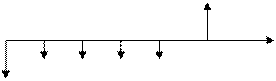 Накопление периодическими взносами (формирование денежных фондов). В начале срока финансовой сделки вносится вклад в размере PV и через равные промежутки времени к нему добавляются суммы С. К концу срока сделки с учетом начисленных процентов накопится сумма FV. Эту ситуацию можно записать (-PV, -С, -С,…-С, FV) и изобразить графически
Накопление периодическими взносами (формирование денежных фондов). В начале срока финансовой сделки вносится вклад в размере PV и через равные промежутки времени к нему добавляются суммы С. К концу срока сделки с учетом начисленных процентов накопится сумма FV. Эту ситуацию можно записать (-PV, -С, -С,…-С, FV) и изобразить графически
|
Анализ потока платежей предполагает решение
а) прямой задачи, когда проводится оценка с позиции будущего, т. е. вычисляется сумма всех платежей с начисленными процентами на конец срока проведения операции;
б) обратной задачи, когда проводится оценка с позиции настоящего, т. е. определяется современная стоимость всех платежей, приведенная на момент начала операции.
БУДУЩАЯ СУММА ПРЕНУМЕРАНДО И ПОСТНУМЕРАНДО БЕЗ ПЕРВОНАЧАЛЬНОЙ СУММЫ
Рента пренумерандо
Пусть одинаковые платежи размером С (cost – стоимость) осуществляются пренумерандо в течение n периодов. На них нарастают проценты по номинальной (ежегодной) процентной ставке r. Сначала рассмотрим С по абсолютной величине.
В начале первого периода осуществлен взнос С. К концу периода на него нарастут проценты, и будущая сумма составит
FV1 = С·(1 + r).
В начале второго периода внесена сумма С, а к концу второго периода на нее и на FV1опять нарастут проценты
FV2=С·(1+r)+С·(1+r)2.
К концу третьего периода
FV3 = С·(1+r)+С·(1+r)2+С·(1+r)3 и т. д.
К концу n-ого периода будущая сумма составит
 FVn = С· (1+r)+С· (1+r)2+ . . . +С· (1+r)n = С· (1+r) ·
FVn = С· (1+r)+С· (1+r)2+ . . . +С· (1+r)n = С· (1+r) · 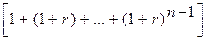 .
.
Нетрудно видеть, что это сумма геометрической прогрессии с общим членом
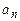 =
= 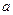 1·qn -1, где
1·qn -1, где 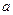 1=С· (1+r), a q=1+r.
1=С· (1+r), a q=1+r.
Как известно из школьного курса [7], сумма такой геометрической прогрессии
Sn= 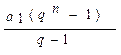 .
.
Таким образом, получаем
FVn= 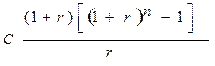
 .
.
Если взносы осуществляются m раз в году в течение k лет, то число периодов сделки n=k·m, а процентная ставка за период составляет r/m. В этом случае
FV= 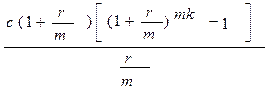 . (2.1)
. (2.1)
Рента постнумерандо
Те же условия, что в разделе 2.2.1, но рента вносится в конце каждого периода – постнумерандо.
К концу первого периода сделан взнос С и FV1=С
К концу второго периода снова сделан взнос С, а на FV1 наросли проценты:
FV2=С+С·(1+r).
К концу третьего: FV3=С+С·(1+r)+С·(1+r)2 и т. д.
Будущая сумма к концу n-ого периода
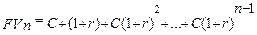 .
.
Это геометрическая прогрессия с первым членом 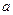 1=С и частным q=(1+r). Следовательно,
1=С и частным q=(1+r). Следовательно,
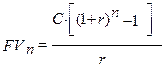 .
.
Если взносы осуществляются m раз в году в течение k лет, то n=m·k
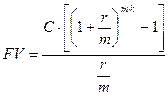 . (2.2)
. (2.2)
Формулы (2.1) и (2.2) можно объединить в одну.
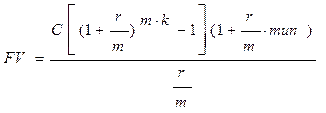 (2.3)
(2.3)
Здесь тип=0, для взносов постумерандо,
тип=1, для взносов пренумерандо.
Очевидно, что при выплатах пренумерандо абсолютная величина будущей накопленной суммы больше.
Поскольку выплаты С и конечная сумма имеют, как правило, разные знаки (-С; -С;-С; FV) или (С; С;С; -FV), то их сводят в уравнение эквивалентности
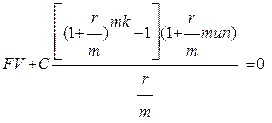 (2.4)
(2.4)
Напомним, что в выражениях (2.1) – (2.4) величина m – это число взносов и начислений процентов в году.
При ежемесячных взносах m=12;
при ежеквартальных взносах m=4;
при взносах раз в полгода m=2;
при ежегодных взносах m=1.
|
 Решение
Решение
С=-300 руб.
r=0,18
k=1
 m=1,2
m=1,2
FV=?
 Второй случай –взносы пренумерандо (тип =1)
Второй случай –взносы пренумерандо (тип =1)
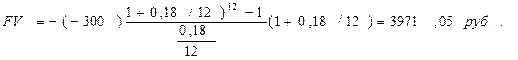
Если бы мы копили эти деньги в банке из под кофе, то в конце года имели бы только
FV=300*12=3600 руб.
Таким образом, в обоих случаях за счет процентов банк нам приплачивает в конце года больше трехсот руб. Однако во втором случае (выплаты в начале каждого месяца) мы получим почти на 60 руб. больше.