Стоимости денег во времени

Финансовый менеджмент требует постоянного осуществления различного рода финансово-экономических расчетов, связанных с по­токами денежных средств в разные периоды времени. Ключевую роль в этих расчетах играет оценка стоимости денег во времени.

Концепция стоимости денег во времени состоит в том, что стоимость денег с течением времени изменяется с учетом нормы прибыли на финансовом рынке, в качестве которой обычно высту­пает норма ссудного процента (или процента).Иными словами, в соответствии с этой концепцией одна и та же сумма денег в разные периоды времени имеет разную стоимость; эта стоимость в настоя­щее время всегда выше, чем в любом будущем периоде.

Концепция стоимости денег во времени играет основополага­ющую роль в практике финансовых вычислений. Она предопределяет необходимость учета фактора времени в процессе осуществления любых долгосрочных финансовых операций путем оценки и сравне­ния стоимости денег при начале финансирования со стоимостью де­нег при их возврате в виде будущей прибыли, амортизационных от­числений, основной суммы долга и т.д.

Оценка стоимости денег с учетом фактора времени требует пред­варительного рассмотрения связанных с ней базовых понятий. Ниже изложено содержание основных из этих понятий.

ПРОЦЕНТ —сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах (депозитный процент, кредитный процент, процент по облига­циям, процент по векселям и т.п.).

ПРОСТОЙ ПРОЦЕНТ—сумма дохода, начисляемого к основной сумме капитала в каждом интервале, по которой дальнейшие расчеты пла­тежей не осуществляются. Начисление простого процента приме­няется, как правило, при краткосрочных финансовых операциях.

СЛОЖНЫЙ ПРОЦЕНТ —сумма дохода, начисляемого в каждом ин­тервале, которая не выплачивается, а присоединяется к основ­ной сумме капитала и в последующем платежном периоде сама

приносит доход. Начисление сложного процента применяется, как правило, при долгосрочных финансовых операциях (инвес­тировании, кредитовании и т.п.).

ПРОЦЕНТНАЯ СТАВКА (СТАВКА ПРОЦЕНТА)— удельный показатель, в соответствии с которым в установленные сроки выплачивает­ся сумма процента в расчете на единицу капитала. Обычно про­центная ставка характеризует соотношение годовой суммы про­цента и суммы предоставленного (заимствованного) капитала (выраженное в десятичной дроби или в процентах)

БУДУЩАЯ СТОИМОСТЬ ДЕНЕГ— сумма инвестированных в настоя­щий момент денежных средств, в которую они превратятся че­рез определенный период времени с учетом определенной ставки процента (процентной ставки).

НАСТОЯЩАЯ СТОИМОСТЬ ДЕНЕГ— сумма будущих денежных средств, приведенных с учетом определенной ставки процента (процент­ной ставки) к настоящему периоду времени.

НАРАЩЕНИЕ СТОИМОСТИ (КОМПАУНДИНГ)— процесс приведения настоящей стоимости денег к их будущей стоимости в опреде­ленном периоде путем присоединения к их первоначальной сумме начисленной суммы процентов.

ДИСКОНТИРОВАНИЕ СТОИМОСТИ— процесс приведения будущей стоимости денег к их настоящей стоимости путем изъятия из их будущей суммы соответствующей суммы процентов (называемой „дисконтом").

ПЕРИОД НАЧИСЛЕНИЯ— общий период времени, в течение которо­го осуществляется процесс наращения или дисконтирования стоимости денежных средств.

ИНТЕРВАЛ НАЧИСЛЕНИЯ— обусловленный конкретный временной срок (в пределах общего периода начисления), в рамках кото­рого рассчитывается отдельная сумма процента по установлен­ной его ставке (осуществляется отдельный платеж процента).

ПРЕДВАРИТЕЛЬНЫЙ МЕТОД НАЧИСЛЕНИЯ ПРОЦЕНТА (МЕТОД ПРЕ-НУМЕРАНДО ИЛИ АНТИСИПАТИВНЫЙ МЕТОД)— способ рас­чета платежей, при котором начисление процента осуществля­ется в начале каждого интервала.

ПОСЛЕДУЮЩИЙ МЕТОД НАЧИСЛЕНИЯ ПРОЦЕНТА (МЕТОД ПОСТНУ-МЕРАНДО ИЛИ ДЕКУРСИВНЫЙ МЕТОД)— способ расчета пла­тежей, при котором начисление процента осуществляется в конце каждого интервала.

ДИСКРЕТНЫЙ ДЕНЕЖНЫЙ ПОТОК— поток платежей на вложенный капитал, имеющий четко ограниченный период начисления про­центов и конечный срок возврата основной его суммы.

НЕПРЕРЫВНЫЙ ДЕНЕЖНЫЙ ПОТОК— поток платежей на вложен­ный капитал, период начисления процентов по которому не огра­ничен, а соответственно не определен и конечный срок возвра­та основной его суммы.

АННУИТЕТ (ФИНАНСОВАЯ РЕНТА)— длительный поток платежей, характеризующийся одинаковым уровнем процентных ставок на протяжении всего периода.

Система основных базовых понятий позволяет последовательно рассмотреть методический инструментарий оценки стоимости денег во времени в разрезе наиболее характерных вариантов осуществле­ния такой оценки. Этот методический инструментарий дифференциру­ется в разрезе отдельных видов вычислений.

I. Методический инструментарий оценки стоимости денег по простым процентамиспользует наиболее упрощенную систему рас­четных алгоритмов.

1. При расчете суммы простого процента в процессе нараще­ния стоимости (компаундинга) используется следующая формула:

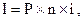
где 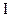— сумма процента за обусловленный период времени в

целом;

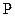— первоначальная сумма (стоимость) денежных средств;

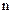— количество интервалов, по которым осуществляется рас­чет процентных платежей, в общем обусловленном пе­риоде времени;

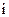— используемая процентная ставка, выраженная десятич­ной дробью.

В этом случае будущая стоимость вклада 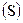с учетом начис­ленной суммы процента определяется по формуле:

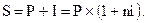
Пример: Необходимо определить сумму простого про­цента за год при следующих условиях: первоначальная сумма вклада — 1000 усл. ден. ед.; процентная ставка, Выплачиваемая ежеквартально — 20%.

Подставляя эти значения в формулу, получим сумму процента: 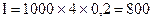усл. ден. ед.; будущая стоимость вклада в этом случае составит:

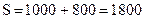усл. ден. ед.

Множитель 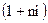называется множителем (или коэффициен­том) наращения суммы простых процентов. Его значение всегда дол­жно быть больше единицы.

2. При расчете суммы простого процента В процессе дис­контирования стоимости (т.е. суммы дисконта) используется сле­дующая формула:

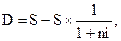
где 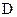— сумма дисконта (рассчитанная по простым процентам)

за обусловленный период времени в целом; 5— стоимость денежных средств;

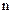— количество интервалов, по которым осуществляется рас­чет процентных платежей, в общем обусловленном пе­риоде времени;

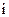— используемая дисконтная ставка, выраженная десятич­ной дробью.

В этом случае настоящая стоимость денежных средств 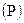с уче­том рассчитанной суммы дисконта определяется по следующим фор­мулам:

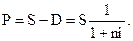
Пример: Необходимо определить сумму дисконта по простому проценту за год при следующих условиях: конечная сумма вклада определена 8 размере 1000 усл. ден. ед.; дисконтная ставка составляет 20% 8 квартал.

Подставляя эти значения в формулу расчета суммы дисконта, получим:

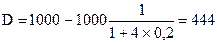усл. ден. ед.

Соответственно настоящая стоимость вклада, не­обходимого для получения через год 1000 усл. ден. единиц, должна составить:

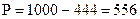усл. ден. ед.

Используемый в обеих случаях множитель 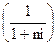называется

дисконтным множителем (коэффициентом) суммы простых процен­тов, значение которого всегда должно быть меньше единицы.

II. Методический инструментарий оценки стоимости денег по сложным процентамиспользует более обширную и более усложнен­ную систему расчетных алгоритмов.

1. При расчете будущей суммы вклада (стоимости денежных средств) в процессе его наращения по сложным процентам исполь­зуется следующая формула:

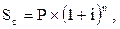
где 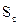— будущая стоимость вклада (денежных средств) при его

наращении по сложным процентам;

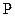— первоначальная сумма вклада;

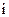— используемая процентная ставка, выраженная десятич­ной дробью;

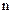— количество интервалов, по которым осуществляется каж­дый процентный платеж, в общем обусловленном пери­оде времени.

Соответственно сумма процента 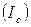в этом случае определяет­ся по формуле:

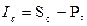
Пример: Необходимо определить будущую стоимость вклада и сумму сложного процента за весь период инвести­рования при следующих условиях: первоначальная стоимость вклада — 1000 усл. ден. ед.; процентная ставка, используемая при расчете суммы слож­ного процента, установлена в размере 20% в квартал; общий период инвестирования — один год.

Подставляя эти показатели в вышеприведенные фор­мулы, получим:

Будущая стоимость вклада =

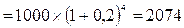усл. ден. ед.

Сумма процента 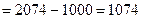усл. ден. ед.

2. При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам используется следующая формула:

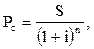
где 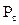— первоначальная сумма вклада;

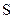— будущая стоимость вклада при его наращении, обуслов­ленная условиями инвестирования;

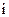— используемая дисконтная ставка, выраженная десятич­ной дробью;

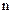— количество интервалов, по которым осуществляется каж­дый процентный платеж, в общем обусловленном пери­оде времени.

Соответственно сумма дисконта (0_С) в этом случае определяет­ся по формуле:

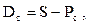
Пример: необходимо определить настоящую стои­мость денежных средств и сумму дисконта по сложным процентам за год при следующих условиях: будущая стоимость денежных средств определена в раз­мере 1000 усл. ден. ед.;

используемая для дисконтирования ставка сложного процен­та составляет 20% в квартал.

Подставляя эти значения в формулы, получим:

Настоящая стоимость =

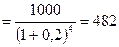усл. ден. ед.

Сумма дисконта 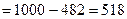усл. ден. ед.

3. При определении средней процентной ставки, используе­мой в расчетах стоимости денежных средств по сложным процен­там, применяется следующая формула:

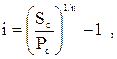
где 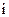— средняя процентная ставка, используемая в расчетах сто­имости денежных средств по сложным процентам, выра­женная десятичной дробью;

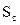— будущая стоимость денежных средств;

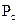— настоящая стоимость денежных средств;

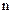— количество интервалов, по которым осуществляется каж­дый процентный платеж, в общем обусловленном периоде времени.

Пример: необходимо определить годовую ставку до­ходности облигации при следующих условиях: номинал облигации, подлежащий погашению через три года, составляет 1000 усл. ден. ед.;

цена, по которой облигация реализуется в момент ее эмис­сии, составляет 600 усл. ден. ед.

Подставляя эти значения в формулу, получим:

годовая ставка доходности =

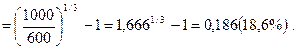
4. Длительность общего периода платежей, выраженная ко­личеством его интервалов, в расчетах стоимости денежных

средств по сложным процентам определяется путем логарифмиро­вания по следующей формуле:

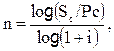
где 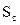— будущая стоимость денежных средств;

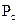— настоящая стоимость денежных средств;

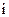— используемая процентная ставка, выраженная

десятичной дробью.

5. Определение эффективной процентной ставки в процессе наращения стоимости денежных средств по сложным процентам осуществляется по формуле:

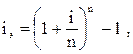
где 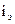— эффективная среднегодовая процентная ставка при на­ращении стоимости денежных средств по сложным про­центам, выраженная десятичной дробью;

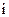— периодическая процентная ставка, используемая при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

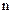— количество интервалов, по которым осуществляется каж­дый процентный платеж по периодической процентной ставке на протяжении года.

Пример: необходимо определить эффективную сред­негодовую процентную ставку при следующих условиях: денежная сумма 1000 усл. ден. ед. помещена в коммерчес­кий банк на депозит сроком на 2 года; годовая процентная ставка, по которой ежеквартально осу­ществляется начисление процента, составляет 10% (0,1).

Подставляя эти значения в формулу, получим:

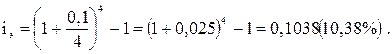
Результаты расчетов показывают, что условия по­мещения денежной суммы сроком на 2 года под 10% годовых при ежеквартальном начислении процентов, равнозначны условиям начисления этих процентов один раз в год под 10,38% годовых (10,38% составляет размер эффективной или сравнимой процентной ставки).

При оценке стоимости денег во времени по сложным процентам необходимо иметь в виду, что на результат оценки оказывает боль-

шое влияние не только используемая ставка процента, но и число интервалов выплат в течение одного и того же общего платежного периода. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большим числом интервалов в течение предусмотренного периода платежа.

Пример: Перед инвестором стоит задача разместить 100 усл. ден. ед. на депозитный Вклад сроком на один год. Один банк предлагает инвестору выплачивать доход по слож­ным процентам В размере 23% в квартал: Второй — В раз­мере 30% один раз В четыре месяца; третий — в размере 45% два раза В году; четвертый — в размере 100% один раз в году.

Для того, чтобы определить, какой Вариант инвести­рования лучше, построим следующую таблицу:

Таблица 3.1.