Расчет влияния факторов на изменение суммы прибыли (убытка) от продажи товаров, продукции, работ, услуг

Подстановки	Взаимодействующие факторы	Сумма прибыли, тыс. руб.	Влияние фактора на сумму прибыли, тыс. руб.
объем продаж	структура продаж	себестои­мость продаж	цены продаж
Исходные данные	предыду­щий год	предыду­щий год	предыду­щий год	предыду­щий год	8 540
Объем продаж отчетного года	отчетный год	предыду­щий год	предыду­щий год	предыду­щий год	7 940*	-600
Структура продаж отчетного года	отчетный год	отчетный год	предыду­щий год	предыду­щий год	8 430	+490
Себестоимость отчетного года	отчетный год	отчетный год	отчетный год	предыду­щий год	8 730**	+300
Цены отчетного года	отчетный год	отчетный год	отчетный год	отчетный год	9 170	+440
Итого						+630

7940 = 8540 х (53 750 : 57 800).

8730 = 8430 - (45 020 - 45 320).

Рассмотренные методы функционального детерминированного анализа прибыли основаны на разложении анализируемого показате­ля на составляющие элементы, но они не учитывают сложные связи, возникающие между прибылью и другими стоимостными качествен­ными показателями: производительностью труда, фондоотдачей, ма­териалоемкостью, качеством продукции.

Анализ системы таких взаимосвязей между показателями предпо­лагает применение стохастического (вероятностного) анализа, к кото­рому относятся корреляционный и регрессионный методы.

Обеспечение точности расчетов влияния факторов на результатив­ный показатель с более высокой статистической надежностью дости­гается путем сведения множества исходных экономических показате­лей к нескольким обобщающим характеристикам, т.е. к комплексным факторам (главным компонентам), на основе которых строится ре­грессионное, уравнение:

(9)

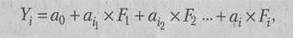где

У; — результативный показатель (прибыль);

Oq — свободный член уравнения;

й, — весовой коэффициент при г-й главной компоненте;

Fj — обобщающий фактор (главная компонента).

Выделенные при статистической обработке исходных данных главные компоненты характеризуют закономерности формирования прибыли. В регрессионном уравнении, построенном на главных ком­понентах, комплексный фактор F_x включает показатели Х_х (произво­дительность труда), Х₂ (численность рабочих) и Х₃ (коэффициент сменности). Тогда комплексный фактор F_i приобретает новую смыс­ловую нагрузку и может быть выражен как уровень использования живого труда. Фактор F₂, включающий показатели фондоотдачи и обора­чиваемости оборотных средств, характеризует использование основных и оборотных производственных фондов, а фактор F₃, включающий показатели материалоемкости и материальных затрат, характеризует уровень использования материальных ресурсов.

Свободный член уравнения, построенного на главных компонен­тах, характеризует среднее значение прибыли в анализируемой сово­купности, поэтому решение уравнения позволяет определить величи­ну прибыли только за счет выделения главных компонент. Значение прибыли в уравнении позволяет проводить сравнительный анализ ра­боты предприятия за несколько лет и установить динамику его рента­бельности.

Методика регрессионного анализа прибыли и других стоимостных показателей требует достаточной репрезентативности данных. В усло­виях отдельного предприятия для обеспечения репрезентативности необходимы данные за несколько лет.

При использовании методов стохастического анализа уравнение регрессии по прибыли принимает линейный вид. В результате реше­ния уравнения по каждому фактору, влияющему на прибыль, получа­ется многофакторная корреляционная модель анализа прибыли:

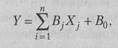(10)

где Y — моделируемый показатель (прибыль);

В_о — свободный член уравнения; Bj — весовой коэффициент при j-м факторе; Xj — фактор.

Определив параметры уравнения, можно выяснить степень зави­симости прибыли от всех включенных в модель факторов. В качестве таких факторов можно принять следующие: затраты на рубль продук­ции, производительность труда, фондоотдачу, материалоемкость, коэффициент сменности, удельный вес сертифицированной, новой или модернизированной продукции, оборачиваемость оборотных или со­вокупных активов, сумму материальных затрат, стоимость основных фондов.

Регрессионный анализ позволяет выявлять такие факторы форми­рования прибыли, которые нельзя установить на основании данных формы № 2. Вместе с тем точность расчетных значений показателя прибыли в регрессионных моделях зависит от числа включенных пе­ременных, увеличение которых снижает статистическую надежность модели.