Тема 6. практическое приложение теории процентных ставок

Консолидирование задолженности.

Пример 22

Два платежа 100 тыс.руб. и 50 тыс.руб. со сроками 150 и 180 дней (отсчитываемых от одной даты) заменяются одним со сроком 200 дней. Используется ставка простых процентов 6% годовых. Найти размер нового платежа.

Решение.

Для первого платежа срок пролонгации составляет 50 дней, для второго 20 дней. Консолидированный платеж находится суммированием наращенных платежей за соответствующие сроки.

S₀ = 100000 (1 + 0,06 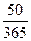) + 50000 (1 + 0,06 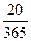) = 150986 (руб.)

Пример 23

Решено консолидировать три платежа 10 тыс.руб., 20 тыс.руб., 15 тыс.руб. со сроками 15.05, 15.06, 15.08., отсчитываемых от одной даты. Срок консолидированного платежа 01.08. этого же года. Найти размер нового платежа при использовании процентной ставки 8% годовых.

Решение.

Первый и второй платежи продляются на 78 и 47 дней соответственно. Следовательно, суммы 10000 руб. и 20000 руб. необходимо нарастить по ставке 8%. Срок третьего платежа сокращается на 14 дней, следовательно, 15000 руб. необходимо дисконтировать.

S₀=10000 (1+ 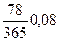) + 20000 (1+ 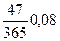) + 15000 (1+ 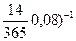=45331 (руб.)

Пример 24

Имеется обязательство уплатить 100000 руб. через 4 месяца и 70000 руб. через 8 месяцев после некоторого момента времени. По новому обязательству необходимо плату произвести равными суммами (S₀) через 3 и 6 месяцев после этого момента. В контракте используется процентная ставка 6% годовых.

Решение.

По новым условиям контракта возможны две даты приведения платежей – конец 3-его месяца и 6-ого месяца по новым условиям контракта. Возьмем в качестве даты приведения конец 3-его месяца. Платежи по старым и новым условиям контракта приводятся на эту дату. Уравнение эквивалентности имеет вид:

100000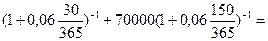

старые условия контракта

=

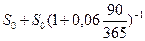
новые условия контракта.

Решая это уравнение, получаем S₀ = 84527 руб. По новым условиям контракта платежи идут равными суммами по 84527 руб. через 3 и 6 месяцев после начального момента времени.

ВНИМАНИЕ! При простом объединении платежей консолидированный платеж находится суммированием отдельных платежей, приведенных на момент времени консолидированного платежа с помощью наращения или дисконтирования по одной и той же процентной ставке. В более сложном случае, когда происходит изменение условий контракта, (см. Пример 20) необходимо использовать уравнение эквивалентности, которое в общем случае строится следующим образом: платежи по старым условиям контракта равны платежам по новым условиям контракта с учетом их приведения по одной и той же процентной ставке к дате по новым условиям контракта.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что понимается под финансовой эквивалентностью обязательств?

2.Почему объединение платежей нельзя провести простым суммированием платежей? Как решается задача консолидирования платежей?

3.Почему предполагается, что все платежи отсчитываются от одной даты? Как решается задача консолидирования разновременных платежей?

4. Как строится уравнение эквивалентности? В каком случае необхлдимо использовать уравнение эквивалентности?

ЗАДАЧИ

1. Два векселя со сроками 10.06 (10 тыс.руб.) и 01.08 (20 тыс.руб.) заменяются одним с продлением срока до 01.10.этого же года. При объединении векселей применена учетная ставка 8%. Сроки пролонгации составляют 113 и 61 день. Определить сумму нового обязательства.

2. Имеются два обязательства. Условия первого: заплатить 400 тыс.руб. через 3 месяца; условия второго: заплатить 500 тыс.руб. через 9 месяцев отсчитываемых от одной даты. Найти консолидированную сумму для нового платежа сроком:

а) 10 месяцев;

б) 1 месяц;

При объединении платежей используется простая процентная ставка 26%

годовых.

3. Два платежа S1 = 100 тыс.руб. и S2 = 50 тыс.руб. со сроками 150 и 180 дней (отсчитываемых от одной даты) заменяются одним со сроком 170 дней. Найти размер консолидированного платежа при использовании простой ставки 26% годовых.

4. Решено консолидировать три платежа со сроками 1.03., 15.04., 20.05., суммы платежей 10, 50, 15 тыс.руб. Срок консолидированного платежа 1.05. этого же года.При объединении платежей используется ставка простых процентов 20 %. Найти размер консолидированного платежа.

5. Обязательства в сумме 100 тыс.руб. и 50 тыс.руб. должны быть погашены соответственно 1.03. и 1.10. текущего года. Стороны согласились пересмотреть условия: должник уплачивает 60 тыс.руб. 1.12 текущего года, остальной долг гасится 1.04. следующего года. Найти сумму нового платежа при условии, что стороны согласились применить в расчетах простую ставку 26%:

а) дата приведения платежей 1.04.;

б) дата приведение платежей 1.12.

6. Обязательства в сумме 100 тыс.руб. со сроками погашения 2 и 4 года были пересмотрены в новых условиях контракта. По новым условиям предусмотрено уплатить долг равными суммами через 1 год и 5 лет, отсчитываемых от одного момента времени. В контракте предусмотрена ставка сложных процентов 5 % годовых. Определить размер новых платежей.

7. Имеются обязательства 10 тыс.руб., 30 тыс.руб. и 45 тыс.руб. со сроками погашения 1 год, 1,5 года и 2 года. Новыми условиями контракта предусмотрено объединение платежей в один со сроком 1,5 года, в контракте используется ставка сложных процентов 5 %. Найти размер консолидированного платежа.

8. Два векселя со сроками погашения 180 дней 10 тыс.руб. и 150 дней 15 тыс.руб. заменяются одним со сроком погашения 280 дней. При объединении векселей применена учетная ставка 15%. Определить размер консолидированного платежа.

9. Организация имеет обязательство к одному и тому же кредитору: уплатить 20.02-162 тыс. руб., 14.06. – 16 тыс. руб. и 15.07. – 284 тыс. руб. Принято решение о замене платежей: 20.09. уплатить 200 тыс. руб., остальные – 20.10. Определите сумму к погашению 20 октября исходя из 40% годовых.

10. По договору необходимо уплатить 5.09. текущего года 10 тыс. руб. и 10.12 текущего года 17 тыс. руб. Стороны договорились пересмотреть условия договора и уплатить одну сумму 1.02 следующего года исходя из ставки 10% годовых. Рассчитайте размер консолидированного платежа, если используется германская схема начисления простых процентов.