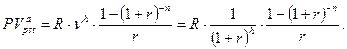Определение процентной ставки

Процентная ставка, являясь показателем доходности финансовой сделки, должна быть определена в процессе ее подготовки. Величину процентной ставки финансовой ренты невозможно определить из выражений: 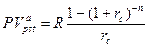и .

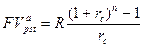Существует ряд математических методов. Рассмотрим метод линейной интерполяции.

а) При известных величинах FV, R и 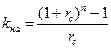= FV/ R

,

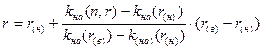где r_(н) и r_(в) – верхнее и нижнее значения предполагаемой процентной ставки;

k_на(r_(в)) и k_на(r_(н)) – значения коэффициентов наращения при использовании процентных ставок r_(н) и r_(в).

в) При известных величинах PV, R и a(n, r), где а(n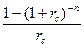,r) = =PV/R

,

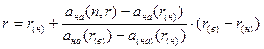где r_(н) и r_(в) – верхнее и нижнее значения предполагаемой процентной ставки;

а_на(r_(в)) и а_на(r_(н)) – значения коэффициентов приведения при использовании процентных ставок r_(н) и r_(в).

Определение параметров других видов рентных платежей

Вечная рента

Если рента не ограничена во времени и имеет неограниченное число членов, то она является вечной рентой. Пример вечной ренты – это выпуск облигационных займов без ограничения срока погашения, доходы по которым выплачиваются через определенные промежутки времени, т.е. эти доходы являются членами ренты.

В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет.

В этом случае прямая задача не имеет смысла, обратная задача (определение приведенной стоимости аануитета) имеет решение. Слагаемые выражения, вычисляющего приведенную стоимость постоянного бессрочного аннуитета представляют собой бесконечно убывающую геометрическую прогрессию с первым членом а₁=R/(1+r) и знаменателем q=1/1+r. Тогда при .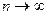

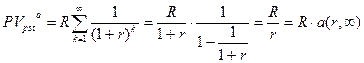Эта формула показывает, что поток даже с неограниченным числом платежей имеет все же конечную приведенную стоимость. С финансовой точки зрения это понятно, поскольку деньги, которые поступят через много лет, сейчас мало что стоят ( а при высокой инфляции практически ничего не стоят).

При сроке аннуитета, превышающем 50 лет, коэффициенты дисконтирования аннуитета незначительно отличаются друг от друга.

Формула используется для оценки целесообразности приобретения бессрочного аннуитета, если известен размер денежного поступления за период. В качестве r обычно применяется гарантированная процентная ставка (например, процент, предлагаемый государственным банком).

Пример. Определить текущую приведенную стоимость бессрочного аннуитета постнумерандо с ежегодным поступлением 4,2 тыс. руб., если предлагаемый государственным банком процент по срочным вкладам равен 14% годовых.

Решение. PV=4,2/0,14=30тыс. руб. Следовательно, если аннуитет предлагается по цене, не превышающей 30 тыс. руб., он представляет собой выгодную инвестицию.

Рассмотрим бессрочный аннуитет постнумерандо с денежными поступлениями р раз за базовый период и начислением сложных процентов m раз за базовый период, получим:

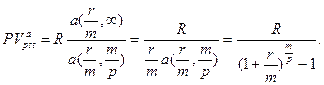
в) Для определения приведенной стоимости бессрочного аннуитета с денежными поступлениями р раз за период и непрерывным начислением процентов по ставке d перейдем к пределу при n®: и получим:

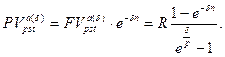
Отложенная рента (отсроченный аннуитет)

Это такая рента, когда срок реализации откладывается на время, указанное в контракте, т.е. первый из потока платежей начинает поступать через h периодов.

Современная величина отложенной ренты является дисконтированной величиной современной величины немедленной ренты по принятой для нее процентной ставке и определяется по следующей формуле: