Шестая функция денежной единицы. Взнос на амортизацию денежной единицы.

Взнос на амортизацию денежной единицы - регулярный платеж в счет погашения денежной единицы кредита и начисленных процентов.

Взнос на амортизацию денежной единицы определяется как величина, обратная текущей стоимости аннуитета:

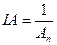(2.18)

где: IA - взнос на амортизацию денежной единицы.

Эта функция применяется при расчете платежей по погашению кредита, если эти платежи предполагаются одинаковыми по величине; при этом каждый платеж включает в себя как выплаты по основной сумме долга, так и начисленные проценты. Единичный платеж в серии

погашающих платежей рассчитывается таким образом:

FVT = PV * IA, (2.19)

где: FVT- будущая стоимость одного платежа в серии выплат кредита и процентов по нему;

PV - текущая стоимость кредита.

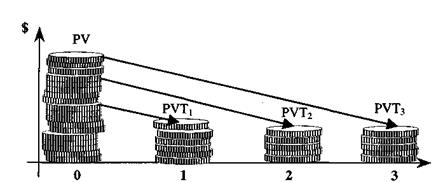
Использование в оценке (пример). Стоимость объекта составляет 100 000. Покупатель использует для приобретения кредитные ресурсы, взятые на 4 года под 15% годовых. Условия возврата кредита - одинаковыми частями каждый год, при этом ежегодно погашается как основная сумма долга, так и проценты по кредиту.

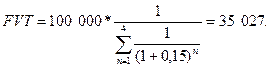(2.20)

Рис. 2.7.Графическое изображение расчета будущей стоимости одинаковых платежей в счет погашения кредита и процентов по нему

Все функции денежной единицы основаны на формуле будущей стоимости денежной единицы. Основной предпосылкой этой формулы является положение о том, что процент начисляется на всю сумму денег, находящуюся на счете, в том числе и на реинвестируемые проценты.

Все функции разделяются на прямые и обратные (см. таблицу 2.2):

Таблица 2.2

Функции денежной единицы

Прямая функция	Обратная функция
будущая стоимость денежной единицы	текущая стоимость денежной единицы
будущая стоимость аннуитета	фактор фонда возмещения
текущая стоимость аннуитета	взнос на амортизацию денежной единицы

Наибольшее применение в оценке находят функции, связанные с переводом денежной суммы из будущего в настоящее время. Это связано с тем, что приведение стоимости осуществляется на дату оценки, то есть к настоящему времени. В этой связи возникает необходимость расчета коэффициента приведения, то есть ставки дисконта, характерного для конкретного оцениваемого объекта.

В ходе оценки, исходя из принципа изменения стоимости, расчеты производятся на конкретную дату. Поэтому приведение доходов в текущую стоимость осуществляется с помощью функций текущей стоимости денежной единицы, рассчитанной на дату оценки следующим образом:

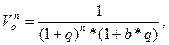(2.21)

где: n - период поступления доходов лет (1...п);

b - дробная часть года, получаемая путем деления количества дней, оставшихся до конца года на общее количество дней в году.

Таблица 2.3

Сводная таблица по шести функциям денежной единицы

Наименование функции денежной единицы	Формула расчета	Примечание
Будущая стоимость денежной		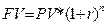Показывает рост $1, положенного на депозит, при накоплении по сложному проценту
Будущая стоимость аннуитета		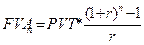Показывает, какой по истечении всего срока будет стоимость серии равных сумм, депонированных в конце каждого из периодических интервалов
Фактор фонда возмещения		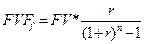Показывает сумму равновеликого периодического взноса, который вместе с процентом необходим для того, чтобы к концу определенного периода накопить $1.
Текущая стоимость денежной единицы		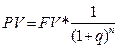Показывает текущую стоимость $1, который должен быть получен единовременно в будущем
Текущая стоимость аннуитета		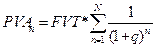Показывает текущую стоимость равномерного потока доходов. Первое поступление происходит в конце первого периода; последующие в конце каждого последующего периода.
Взнос на амортизацию денежной единицы		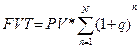Показывает равновеликий периодический платеж, необходимый для полной амортизации кредита.