Задача 8. При изучении покупательского спроса на детские носочки зарегистрирована продажа следующих размеров

10, 11, 13, 11, 10, 11, 12, 13, 13, 12, 11, 10, 11, 12

11, 11, 12, 10, 13, 13, 13, 13, 10, 11, 11, 12, 12, 10

13, 11, 10, 12, 12, 11, 10, 13, 10, 11, 12, 10, 12, 11

11, 11, 12, 10, 10, 10, 11, 12, 13, 13, 12. 10, 11, 12

12, 10, 11, 13, 13, 10, 11, 12, 12, 10, 11, 13, 13, 13

13, 12, 10, 10, 11, 12, 13, 13, 10, 11, 12, 12, 11, 11

11, 13, 10, 12, 12, 12, 10, 10, 13, 13, 13, 10, 11, 12

12, 13, 10, 11, 11, 11, 11, 10, 12, 13, 13, 12, 10, 11

10, 12, 13, 10, 11, 11, 10, 12, 12, 13, 13, 12, 11, 10

12, 11, 11, 10, 12, 12, 13, 10, 11, 11, 11, 12, 13, 12

1. Для обобщения реализованного спроса постройте ряд распределения и проанализируйте полученные результаты, сравнив их с типовой шкалой поставки носочков в магазин

Типовая шкала поставки детских носочков

Размер					Всего
Число пар носочков в % к итогу

2. Данные ряда распределения покупательского спроса и типовой шкалы производства носочков изобразите на графике.

3. Укажите модальную величину ряда распределения.

4. Сделайте выводы в соответствии предложения покупательскому спросу.

Задача 9. При изучении покупательского спроса на одежду зарегистрирована продажа следующих размеров женских брюк

25 27 26 28 25 27 28 26 27 28 28 28 26 25

26 28 26 25 25 26 28 27 26 25 28 28 27 28

25 27 26 26 27 25 28 28 27 26 27 27 25 26

26 27 27 27 28 28 27 26 26 25 27 28 26 28

27 27 28 25 25 25 26 27 28 28 26 26 28 25

27 28 28 28 28 25 25 27 28 26 26 27 28 25

27 27 26 25 25 26 27 27 27 26 28 27 25 25

25 26 26 26 28 28 27 27 28 26 26 25 27 28

26 26 25 27 28 28 27 27 26 25 25 25 26 28

25 27 27 27 28 27 26 25 27 28 27 25 26 27

1. Для обобщения реализационного спроса построим ряд распределения и проанализируем полученные результаты, сравнив их с типовой шкалой поставки одежды

размер					Всего
Число пор в % итого

2. Данными ряда распределения покупательского спроса и типовой шкалы производства одежды изобразить на графике

3. Укажите модальную величину ряда распределения и типовой шкалы

4. Сделайте выводы о соответствии предложения покупательскому спросу.

Задача 10. При изучении покупательского спроса на баскетбольные мячи зарегистрирована продажа следующих размеров

8 5 5 7 5 6 7 6 6 5 5 7 8 8

5 7 6 8 7 6 5 6 5 8 5 6 8 7

5 5 8 6 5 7 8 6 5 6 6 5 5 8

8 6 5 5 7 5 7 7 6 7 7 8 8 6

5 7 7 6 7 5 7 6 8 7 8 8 6 7

5 6 8 8 7 5 5 6 8 7 5 8 6 8

8 7 8 7 8 7 6 5 7 5 6 7 6 7

8 7 7 7 7 7 7 5 7 8 6 7 7 5

6 5 8 5 8 6 5 8 8 7 7 6 7 8

7 7 6 5 7 7 7 8 5 6 8 5 5 6

1. Доля обобщения реализованного спроса постройте ряд распределения, проанализируйте результаты, сравнив их с типовой шкалой поставки баскетбольных мячей

Типовая шкала :

Размер					Всего
количество					100 %

2. Данные ряда распределения покупательского спроса и типовой шкалы производства баскетбольных мячей изобразите на графике

3. Укажите модальную величину ряда распределения и типовой шкалы

4. Сделайте выводы о соответствии спроса и предложения.

Задача 11. Данные внешней торговли РФ (в миллиардах долларов США) составляли за 1995 по 2010 годы:

145.0	157.8	158.9	132.4	115.1	149,9	155,6	168,3
212,0	280,6	369,2	467.8	577.9	763.5	495.2	649.2

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 12. Данные сальдо торгового баланса внешней торговли РФ (в миллиардах долларов США) составляли за 1995 по 2010 годы:

19.8	21.6	14.9	16.4	36.1	60,1	48,1	46,3
59,9	85,8	118,4	139.3	130.9	179.7	111.6	151.7

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 13. Данные внешней торговли РФ по экспорту (в миллиардах долларов США) составляли за 1995 по 2010 годы:

82.4	89.7	86.9	74.4	75.6	105,0	101,9	107,3
135,9	183,2	243,8	303.6	354.4	471.6	303.4	400.4

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте по экспорту на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 14. Данные внешней торговли по странам дальнего зарубежья по экспорту (в миллиардах долларов США) составляли за 1995 по 2010 годы:

65.4	71.1	67.8	58.7	63.6	90,8	86,6	90,9
114,6	153,0	210,2	260.2	300.6	400.5	255.2	337.8

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 15. Данные внешней торговли РФ по импорту (в миллиардах долларов США) составляли за 1995 по 2010 годы:

62.6	68.1	72.0	58.0	39.5	44,9	53,8	61,0
76,1	97,4	125,4	164.3	223.5	291.9	191.8	248.7

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте по импорту на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 16. Данные внешней торговли по странам дальнего зарубежья по импорту (в миллиардах долларов США) составляли за 1995 по 2010 годы:

44.3	47.3	53.4	43.7	29.2	31,4	40,7	48,8
61,0	77,5	103,5	140.2	191.7	252.9	167.7	213.6

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 17. Данные внешней торговли со странами СНГ по импорту (в миллиардах долларов США) составляли за 1995 по 2010 годы:

18.3	20.8	18.6	14.3	10.4	13,4	13,0	12,2
15,1	19,9	21,9	24.0	31.8	39.0	24.1	35.2

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте по импорту на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 18. Данные внешней торговли со странам СНГ по экспорту (в миллиардах долларов США) составляли за 1995 по 2010 годы:

17.0	18.6	19.1	15.8	12.0	14,3	15,3	16,4
21,4	30,2	33,5	43.4	53.8	71.1	48.1	62.6

На основе этих данных:

1. Постройте интервальный ряд распределения, предварительно разбив все данные о внешнеторговом обороте на 4 группы.

2. Определите по данным ряда распределения показатель среднего оборота, среднеквадратическое отклонение и коэффициент вариации.

3. Изобразите полученный вариационный ряд графически с помощью гистограммы распределения.

4. Сделайте выводы.

Задача 19. Имеются данные в процентах о содержании хлопка в 50 образцах мужских рубашек

1. Достроить ряд распределения, разбив все данные на 5 групп с равными интервалами.

2. По данным ряда распределения вычислим среднее содержание хлопка среднее квадратическое отклонение и коэффициент вариации.

3. Указать модальный интервал ряда распределения и моду.

4. Данные о содержании хлопка представить на графике.

Задача 20

Имеются данные в % о содержании хлопка в 50 пуловерах фирмы «Olsen».

4,1	5,5	4,7	4,3	4,5	4,7	4,5	4,3	4,7	4,3
4,7	4,7	6,1	4,7	5,2	5,2	5,5	4,9	4,5	5,5
6,1	5,8	4,9	4,7	4,9	4,5	5,8	4,7	5,8	4,7
4,5	6,1	5,8	4,3	6,1	4,3	6,1	5,2	4,3	5,8
4,9	4,7	4,7	6,1	5,8	4,7	4,5	5,5	6,1	5,2

1. Построить ряд распределения, разбив все данные на 4 группы с равными интервалами.

2. По данным ряда распределения вычислить среднее содержание хлопка, среднее квадратическое отклонение и коэффициент вариации.

3. Укажите модальный интервал ряда распределений и моду.

4. Данные о содержании хлопка представить на графике.

Тестовые вопросы к главе 3

2013452 Ранжированный ряд – это ряд:

1. На основании, которого можно построить огиву;

2. В котором элементы ряда расположены в порядке возрастания или убывания признаков;

3. С непрерывно меняющими значениями вариант;

4. В котором все элементы ряда равны среднему значению;

5. В котором можно найти максимальное и минимальное значение элементов ряда.

2022315 Ряды распределения характеризуют: а) структуру совокупности по какому-либо признаку, б) изменение характеристики совокупности во времени. В процессе их анализа закономерность распределения: в) количественно измеряется, г) изменяется во времени.

1. а, в;

2. а, г;

3. б, в;

4. б, г;

5. Нет правильного ответа.

2031453 Закономерность распределения проявляется в зависимости: а) между вариантами; б) между вариантами и частотами. Она представляет собой отражение: в) общих причин и условий, характерных для всей совокупности: г) общей тенденции развития изучаемого явления.

1. а, в;

2. а, г;

3. б, в;

4. б, г;

5. Нет правильного ответа

2042135 Статистический ряд – это ряд:

1. Динамики, который получен в результате обработки первичных статистических данных и представляющих собой ряд цифровых показателей во времени;

2. Распределения, в котором представлены упорядоченные единицы совокупности по группам;

3. Который получен в результате обработки и систематизации первичных статистических материалов и представляющих собой ряд цифровых показателей, которые характеризуют отдельные стороны изучаемых явлений или процессов;

4. В котором элементы расположены в порядке возрастания или убывания признаков;

5. В котором можно найти максимальное и минимальное значение элементов ряда.

2052314 Вариацией называются: а) различие индивидуальных значений какого-либо признака внутри совокупности: б) различные значения нескольких признаков отдельной единицы совокупности.

1. а;

2. б;

3. а, б;

4. Нет правильного ответа.

5.

2062134 Размах вариации представляет собой абсолютную разность между:

1. Максимальным значением признака и средней величины;

2. Минимальным значением признака и средней величины;

3. Максимальным и минимальным значениями признака;

4. Индивидуальным значениям признака и средней величины;

5. Нет правильного ответа.

2071435 По своему содержанию статистические ряды делятся на:

1. Ряды динамики, ранжированные ряды;

2. Числовые ряды, ряды качественных показателей;

3. Ряды распределения, ранжированные ряды;

4. Ряды динамики, ряды распределения;

5. Ряды непрерывные, ряды прерывные.

2081325 Дисперсия представляет собой: а) средний размер отклонений индивидуальных значений признака от средней; б) средний квадрат этих отклонений. Она может быть рассчитана: в) только для количественного признака; г) для количественного и альтернативного признака.

1. а, в;

2. а, г;

3. б, в;

4. б, г;

5. Нет правильного ответа.

2091234 Урожайность винограда «Рислинг» с одного куста характеризуется следующими данными: = 8кг, = 73кг. Определить среднее квадратическое отклонение урожайности винограда.

1. 9

2. 3

3. 8,5

4. 8

5. 10

2102134 Ряд распределения – это:

1. Ряд, в котором представлены упорядоченные единицы совокупности по группам;

2. Ряд, полученный в результате обработки первичных статистических данных и расположенный в порядке возрастания признака;

3. Ряд распределения, представляющий упорядоченное распределение единицы совокупности на группы по какому-либо варьирующему признаку;

4. Ряд последовательно расположенных в хронологическом порядке показателей, которые характеризуют развитие явлений во времени;

5. Ряд обобщающих показателей.

2111234 Товарные запасы в среднем на 1 кв.м общей площади 20 магазинов составили 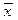= 300 ден.ед., а = 91 600. Определить дисперсию среднего товарного запаса на 1 кв.м общей площади магазинов.

1. 40;

2. 1 600;

3. 2,2;

4. 2,8;

5. 20.

2121413 На основании данных о естественной убыли товара получили: 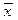= 0,8%; = 0,68%. Определить среднее квадратическое отклонение процента естественной убыли товара.

1. 0,04;

2. 0,12;

3. 0,83;

4. 0,2;

5. Нет правильного ответа.

2131235 Вариационный ряд – это:

1. Это ряд, в котором представлены упорядоченные единицы совокупности;

2. Это ряд распределения, составленный по количественному признаку;

3. Это ряд, в котором варианты принимают значение целых чисел;

4. Это ряд, в котором варианты даются в виде интервала «от - до»;

5. Это ряд, в котором частоты задаются количественными показателями.

2141235 При непрерывной вариации признака целесообразно построить:

1. Дискретный вариационный ряд;

2. Интервальный вариационный ряд;

3. Ряд распределения;

4. Ряд динамики;

5. Нет правильного ответа.

2151234 Межгрупповая дисперсия s²= характеризует вариацию: а) групповых средних; б) индивидуальных значений признака внутри выделенных групп. Среднюю из групповых дисперсий характеризует вариации: