Колеблемость динамических рядов

Основная тенденция пока­зывает, как систематические факторы воздействуют на уровень ряда динамики, а колеблемость уровней тренда служит мерой воздействия остаточных факторов.

Мерой колеблемости динамического ряда выступает средний квадрат отклонений фактических уровней, исчисленных по тренду. Ее можно измерить показателем среднего квадратического отклонения.

Относительной мерой колеблемости является коэффициент вариации, равный отношению среднего квадратического отклонения к среднему уровню ряда.

Измерение сезонных колебаний. При анализе рядов динамики большое значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или несколько лет. При изучении сезонных колебаний используются специальные показатели — индексы сезонности ( ): ,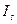

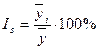где 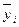- средняя для каждого месяца за изучаемый период;

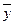- общий средний месячный уровень за изучаемый период.

Совокупность исчисленных для каждого годового цикла индексов сезонности характеризует сезонную волну развития явления во внутригодовой динамике и наглядно может быть представлена графиче­ским методом. При наличии ярко выраженной тенденции развития (увеличение или уменьшение уровней из года в год) применимы дру­гие способы измерения сезонных колебаний, в частности, индексы сезонности определяются на основе методов, которые позволяют исключать влияние тенденции роста (падения).

В таких случаях фактические данные сопоставляются с выравнен­ными, и индексы сезонности определяются по формуле:

,

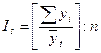где 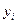- исходные уровни ряда;

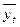- выравненные (теоретические) уровни ряда;

n - число годовых периодов.

Покажем расчет индекса сезонности на примере.

Пример. Имеются следующие данные по строительной фирме об объ­еме выполненных работ по месяцам 2007—2009 гг. по сметной стоимости.

(млн. руб.)

Месяц	Год	В среднем за три года	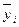Индекс сезонности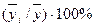
Январь	1.7	1,9	2,0	1,9	67,9
Февраль	1,8	2,1	2,3	2,1	75,0
Март	2,1	2,4	2,8	2,4	85,7
Апрель	2;4	2,6	2,9	2,6	92,9
Май	2,6	2,6	3,0	2,8	100,0
Июнь	2,8	3,0	3,2	3,0	107,1
Июль	3,2	3,3	3,4	3,3	117,9
Август	3,4	3,5	3,4	3,4	121,4
Сентябрь	3,2	3,3	3,0	3,2	114,3
Октябрь	2,9	3,1	3,2	3,1	110,7
Ноябрь	2,7	2,7	3,1	2,8	100,0
Декабрь	2,6	2,5	2,7	2,6	92,9
Средний уровень ряда ( 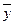)	2,6	2,8	2,9	2,8	100,0

Для ряда внутригодовой динамики, в которой основная тенден­ция роста незначительна, изучение сезонности основано на методе постоянной средней, являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца.

Однако помесячные данные одного года из-за элемента случайнос­ти могут быть ненадежными для выявления закономерности колеба­ний. Поэтому на практике используются помесячные данные за ряд лет (обычно не менее трех лет). Тогда для каждого месяца рассчитывает­ся средняя величина уровня за три года, затем определяются среднеме­сячный уровень для всего ряда и отношение средних для каждого меся­ца к общему среднемесячному уровню ряда (в процентах).

Для получения 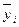проведем усреднение уровней одноименных периодов по формуле простой средней арифметической:

январь - 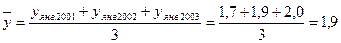(млн руб.);

февраль - 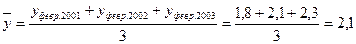(млн руб.);

декабрь - 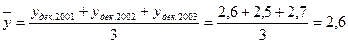(млн руб.).

Осредненные значения уровней ряда 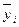для каждого месяца годового цикла представлены в таблице данного примера.

Далее по исчисленным месячным средним уровням 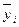определяем 1 общий средний уровень :

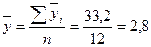(млн руб.),

где n – число месяцев.

Значение общего среднего уровня можно вычислить также по итоговым данным за отдельные годы:

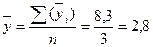(млн руб.),

где n - число лет.

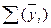- сумма среднегодовых уровней ряда динамики;

В завершение определим индексы сезонности по месяцам года по формуле :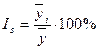

январь - ;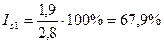

февраль - 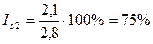и т.д.

Рассчитанные индексы сезонности представлены в таблице примера. Следовательно, минимальный объем выполненных работ строитель­ная фирма имела в январе, а максимальный — в августе.