Типовые примеры и методы их решения. Пример 3.3.1. Работник заключает с фирмой пенсионный контракт на 12 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет
Пример 3.3.1. Работник заключает с фирмой пенсионный контракт на 12 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет поступать по 3 тыс. руб. Требуется определить наращенную сумму к концу действия контракта, если на поступающие суммы будут начисляться: а) ежегодно сложные проценты по номинальной годовой процентной ставке 24%; б) ежеквартально сложные проценты по номинальной годовой процентной ставке 24%; в) непрерывны, проценты с силой роста 24% за год.
Решение.Денежные поступления образуют постоянный аннуитет постнумерандо с А = 3 тыс. руб., сроком п = 12 лет и периодом и = 2 года. Следовательно, период аннуитета больше базового периода начисления процентов, равного году. Схематично это выглядит таким образом:
3 3 3 3 3 3
 |
0 1 2 3 4 5 6 7 8 9 10 11 12 t лет
а) В этом случае r = 24%, m = 1 и по формуле (146) получим:
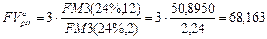 тыс. руб.
тыс. руб.
б) Поскольку в этом случае начисление процентов ежеквартальное, то m = 4 и по формуле (146) получим:
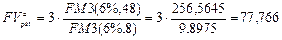 тыс. руб.
тыс. руб.
в) Полагая 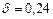 , по формуле (149) находим:
, по формуле (149) находим:
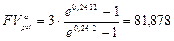 тыс. руб.
тыс. руб.
Пример 3.3.2. Определите сумму, которую необходимо поместить на счет в банке, чтобы в течение 15 лет в конце каждого трехлетнего периода иметь возможность снимать со счета 8 тыс. руб., причем к концу срока полностью выбрать все деньги со счета, если на находящиеся на счете денежные суммы будут начисляться: а) ежегодно сложные проценты по ставке 20%; б) каждые полгода сложные проценты по ставке 20%; в) непрерывные проценты с силой роста 20%.
Решение. Во всех случаях надо определить приведенную стоимость постоянного аннуитета с А = 8 тыс. руб., периодом u = 3 года и сроком n = 15 лет.
а) Так как r =20%, то, применяя формулу (147) при m = 1, получим:
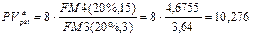 тыс. руб.
тыс. руб.
б) В этом случае m = 2, r = 20%, и поэтому из формулы (147) следует, что:
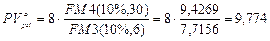 тыс. руб.
тыс. руб.
в) Поскольку в этом случае начисляются непрерывные проценты с силой роста 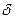 = 0,2 , то по формуле (150) получим:
= 0,2 , то по формуле (150) получим:
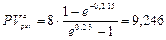 тыс. руб.
тыс. руб.
Пример 3.3.3. На счет в банке в начале каждого двухлетнего периода будет поступать по 8 тыс. руб. в течение 10 лет. Требуется определить: а) будущую стоимость аннуитета; б) приведенную стоимость аннуитета, если на поступающие суммы будут ежегодно начисляться декурсивные сложные проценты по ставке 22% годовых.
Решение. Согласно условию имеем аннуитет пренумерандо с членом А = 14 тыс. руб., периодом u = 2 года и сроком n = 10 лет. Сложная процентная ставка r = 22% годовых и число начислений процентов m = 1.
а) В соответствии с формулами (146) и (152) получим:
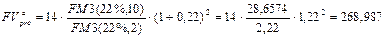 тыс. руб.
тыс. руб.
б) По формулам (147) и (153):
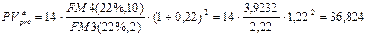 тыс. руб.
тыс. руб.
Пример 3.3.4. Предприниматель приобрел оборудование в кредит за 900 тыс. руб. под 25% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать долг нужно равными суммами в конце каждого второго года и им платить весь долг за 10 лет. Требуется определить величину каждого платежа и составить план погашения долга.
Решение.Обозначим через А величину каждого искомого платежа. Поток этих платежей представляет собой аннуитет постнумерандо, для которого 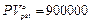 руб., r = 25%, п = 10, m = 1, u = 2. Поэтому для нахождения величины А можно пользоваться формулой (147), из которой следует:
руб., r = 25%, п = 10, m = 1, u = 2. Поэтому для нахождения величины А можно пользоваться формулой (147), из которой следует:
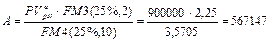 руб.
руб.
Теперь поясним составление плана погашения долга. Поскольку в течение первых двух лет предприниматель пользовался кредитом в размере 900000 руб., то платеж, который равен 567147 руб. и будет сделан в конце второго года, состоит из следующих двух частей: сложных процентов за два года в сумме 506250 руб. ( 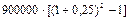 руб.) и погашаемой части долга в сумм 567147 - 506250 = 60897 руб. В следующем двухлетии расчет будет повторен при условии, что размер кредита, которым пользу предприниматель, составит уже меньшую сумму по сравнению с первыми двумя годами, а именно: 900000 - 60897 = 839103 руб. Таким образом, сложные проценты за два года будут равны 471995руб. (
руб.) и погашаемой части долга в сумм 567147 - 506250 = 60897 руб. В следующем двухлетии расчет будет повторен при условии, что размер кредита, которым пользу предприниматель, составит уже меньшую сумму по сравнению с первыми двумя годами, а именно: 900000 - 60897 = 839103 руб. Таким образом, сложные проценты за два года будут равны 471995руб. ( 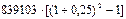 руб.), а погашаемая часть долга будет равна 567147 – 471995 = 95152 руб. и т.д. Ясно, что с течением времени сумма уплачиваемых процентов снижается, а доля платежа в счет погашения долга возрастает.
руб.), а погашаемая часть долга будет равна 567147 – 471995 = 95152 руб. и т.д. Ясно, что с течением времени сумма уплачиваемых процентов снижается, а доля платежа в счет погашения долга возрастает.
План погашения долга представим в виде таблицы
| Номер двухлетия | Остаток ссуды на начало двухлетия | Величина платежа | В том числе | Остаток ссуды на конец двухлетия | |
| проценты за два года | погашенная часть долга | ||||
Поскольку данные в ходе вычислений округлялись, величина процентов в последней строке найдена балансовым методом, т.е. вначале записываем погашенную часть долга 362972 руб., а затем определяем величину процентов за два года: 567147 – 362972 = 204175 руб. Если же непосредственно найти сложные проценты за два года от суммы в 362972 руб. исходя из процентной ставки 25%, то получим 204172 руб. Суммируя величины в пятом столбце, получим размер кредита: 900000 руб.
ПРИЛОЖЕНИЯ
Приложение 1
Сводка основных формул
· Процентная ставкаrt = 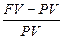 , (1)
, (1)
где PV — предоставляемая в долг сумма,
FV — возвращаемая сумма.
· Учетная ставкаdt = 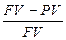 (2)
(2)
· Соотношения между ставками:rt = 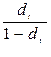 или dt =
или dt = 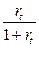 (3)
(3)
· Дисконт-фактор:n = 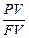 (4)
(4)
· Индекс роста капитала: Bt = 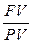 (5)
(5)
· Формула вычисления процентов «со 100»: Q’=Q∙r (6)
· Формула вычисления процентов «на 100»: 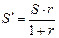 (7)
(7)
· Формула вычисления процентов «во 100»: 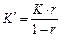 (8)
(8)
· Формула наращение простыми процентами:
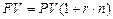 (9)
(9)
· 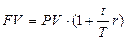 Формула простых процентов в случае нецелого числа лет вид:
Формула простых процентов в случае нецелого числа лет вид:
(10)
Возможны три варианта начисления:
а) точный процент с точным числом дней, обозначаемый как 365/365 или ACT/ACT;
б) обыкновенные проценты с точным числом дней, обозначаемые как 365/360 или АСТ/360 (t - точное, T=360);
в) обыкновенные проценты с приближенным числом дней, обозначаемые как 360/360 (t - приблизительное, считается, что в месяце 30 дней, T = 360).
· Дивизор: 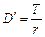 (11)
(11)
· Формулы для вычисления процентного платежа (при использовании простой ставки):
а) если известна величина капитала (P): I = P . l . r; (12)
б) если известна величина капитала, увеличенного на процентный платеж (P+I):
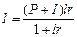 или
или 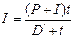 ; (13)
; (13)
в) если известна величина капитала, уменьшенного на процентный платеж (P-I):
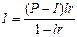 или
или 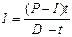 (14)
(14)
· Формула наращения простыми процентами по переменной процентной ставке:
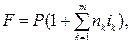 (15)
(15)
где на период nk установлена ставка ik и таких периодов m.
· Формула определения простой процентной ставки, доставляющей при наращении такой же результат, как и несколько простых процентных ставок:
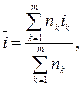 (16)
(16)
где на период nk установлена ставка ik и таких периодов m.
· Формула определения величины начисленных процентов за пользование кредитом с учетом уменьшения долга с течением времени:
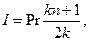 (17)
(17)
где k – число погасительных платежей в год, n – срок кредита.
· Формула приведенной стоимости (при использовании простой ставки):
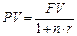 (18)
(18)
· Формула дисконтирования по простой учетной ставке:
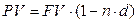 (19)
(19)
· Формула наращения по простой учетной ставке:
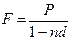 , (20)
, (20)
· Формула для определения срока ссуды (при использовании простой ставки):
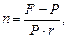 или
или 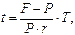 (21)
(21)
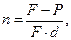 или
или 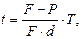 (22)
(22)
· Формулы для определения простой ставки:
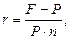 или
или 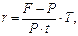 (23)
(23)
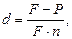 или
или 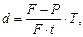 (24)
(24)
· Эквивалентность простых ставок:
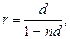 (25)
(25)
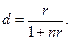 (26)
(26)
· Эквивалентность простых ставок при разных временных базах:
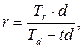 (27)
(27)
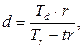 (28)
(28)
где Tr, Td – временные базы, равные количеству дней в году при использовании соответственно процентной и учетной ставок.
· Формулы определения средних значений:
а) простой процентной ставки:
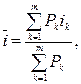 (29)
(29)
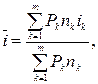 (30)
(30)
б) срока:
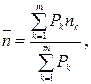 (31)
(31)
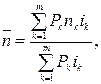 (32)
(32)
где i1, i2, …, im – простые процентные ставки, под которые взяты соответственно суммы P1, P2,…,Pm на сроки где n1, n2, …, nm.
· Формулы для определения средних значений:
а) простой учетной ставки:
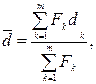 (33)
(33)
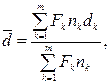 (34)
(34)
б) срока:
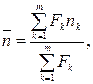 (35)
(35)
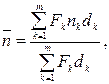 (36)
(36)
где d1, d2, …, dm – простые учетные ставки, по которым соответственно суммы F1, F2,…,Fm учитываются за сроки где n1, n2, …, nm.
· Формула наращения простыми процентами с учетом уплаты налога:
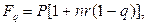 (37)
(37)
где q – ставка налога на проценты.
· Формула наращения по простой учетной ставке с учетом уплаты налога:
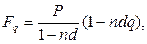 (38)
(38)
где q – ставка налога на проценты.
· Индекс цен (индекс инфляции):
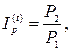 (39)
(39)
где P1, P2 – стоимости потребительской корзины в начале и в конце периода длительностью t.
· Темп инфляции:
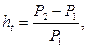 (40)
(40)
где P1, P2 – стоимости потребительской корзины в начале и в конце периода длительностью t.
· Соотношение между индексом инфляции и темпом инфляции:
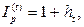 (41)
(41)
· Формула определения индекса инфляции за период при известных индексах инфляции за составляющие его подпериоды:
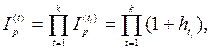 (42)
(42)
где Ip(ti) ,(hti) – индекс инфляции (темп инфляции) за подпериод ti, подпериоды расположены последовательно друг за другом и t = t1 + t2 +…+tk.
· Формула наращения простыми процентами учетом инфляции:
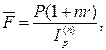 (43)
(43)
где Ip(n) – индекс инфляции за период n.
· Формулы определения простой годовой процентной ставки, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной ставке r:
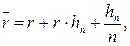 (44)
(44)
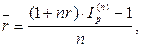 (45)
(45)
где hn – темп инфляции за период n,
Ip(n) – индекс инфляции за период n.
· Формулы определения реальной годовой процентной ставки, при объявленной номинальной процентной ставке в условиях инфляции:
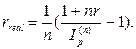 (46)
(46)
· Формулы определения простой годовой учетной ставки, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной ставке d:
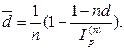 (47)
(47)
· Формулы определения реальной годовой учетной ставки, при объявленной номинальной учетной ставке в условиях инфляции:
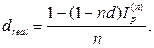 (48)
(48)
· Формула для вычисления величины нового платежа при использовании простой процентной ставки:
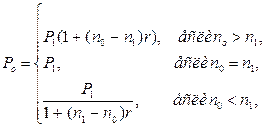 (49)
(49)
где P1 и n1 – первоначальный платеж и срок его выплаты, n0 – срок выплаты нового платежа.
· Формула для вычисления срока нового платежа при использовании простой процентной ставки:
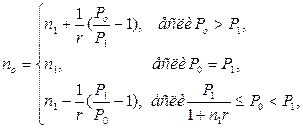 (50)
(50)
где P1 и n1 – первоначальный платеж и срок его выплаты, P0 – величина нового платежа.
· Формула определения срока консолидированного платежа при использовании простой процентной ставки:
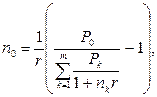 (51)
(51)
где платежи P1, P2,…,Pm, уплачиваемые соответственно через время n1, n2,…, nm заменяются одним платежом P0.
· Формула для вычисления величины нового платежа при использовании простой учетной ставки:
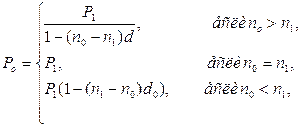 (52)
(52)
где P1 и n1 – первоначальный платеж и срок его выплаты, n0 – срок выплаты нового платежа.
· Формула для вычисления срока нового платежа при использовании простой учетной ставки:
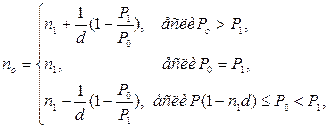 (53)
(53)
где P1 и n1 – первоначальный платеж и срок его выплаты, P0 – величина нового платежа.
· Формула определения срока консолидированного платежа при использовании простой учетной ставки:
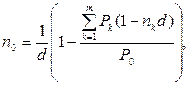 (54)
(54)
где платежи P1, P2,…,Pm, уплачиваемые соответственно через время n1, n2,…, nm заменяются одним платежом P0.
· Формула наращения сложными процентами:
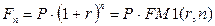 (55)
(55)
где n - число периодов начисления сложных процентов.
· Формула наращения сложными процентами по переменной процентной ставке:
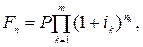 (56)
(56)
где nk –количество периодов начисления сложных процентов по процентной ставке ik , n – общий срок наращения.
· Формула наращения по смешанной схеме:
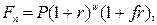 (57)
(57)
где w – целое число периодов начисления сложных процентов, f – дробная часть периода, n = w+f.
· Формула наращения сложными процентами при начислении процентов несколько раз в год:
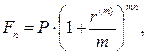 (58)
(58)
где n – число лет, m – количество начислений в год.
· Формула наращения по смешанной схеме при начислении процентов несколько раз в год:
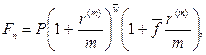 (59)
(59)
где n – число лет, 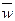 ‑ целое число периодов начисления сложных процентов в n годах,
‑ целое число периодов начисления сложных процентов в n годах, 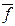 ‑ дробная часть периода,
‑ дробная часть периода, 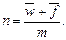
· Формула определения срока ссуды (при использовании сложной процентной ставки):
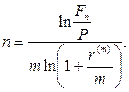 (60)
(60)
· Формулы для определения номинальной годовой процентной ставки:
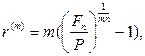 (61)
(61)
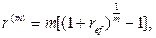 (62)
(62)
где ref – эффективная годовая процентная ставка.
· Формулы определения эффективной годовой процентной ставки:
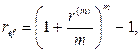 (63)
(63)
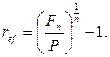 (64)
(64)
· Формула приведенной стоимости (при использовании сложной ставки):
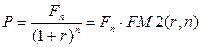 (65)
(65)
· Формула приведенной стоимости (при m-кратном начислении процентов в год):
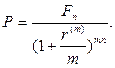 (66)
(66)
· Формула дисконтирования по сложной учетной ставке:
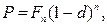 (67)
(67)
где n – число периодов дисконтирования.
· Формула дисконтирования по смешанной схеме:
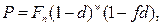 (68)
(68)
где w – целое число периодов дисконтирования по сложной учетной ставке, f – дробная часть периода, n = w+f.
· Формула дисконтирования по сложной учетной ставке, осуществляемого несколько раз в год:
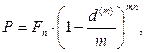 (69)
(69)
где n – число лет, m – количество осуществлений операции дисконтирования в год.
· Формула дисконтирования по смешанной схеме при дисконтировании несколько раз в год:
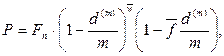 (70)
(70)
где n – число лет, 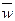 ‑ целое число периодов дисконтирования в n годах,
‑ целое число периодов дисконтирования в n годах, 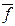 ‑ дробная часть периода,
‑ дробная часть периода, 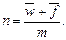
· Формула для определения срока ссуды (при использовании сложной учетной ставки):
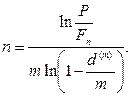 (71)
(71)
· Формулы для определения номинальной годовой учетной ставки:
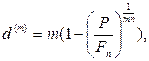 (72)
(72)
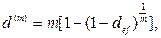 (73)
(73)
где def – эффективная годовая процентная ставка.
· Формулы определения эффективной учетной ставки:
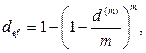 (74)
(74)
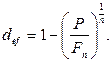 (75)
(75)
· Формула наращения сложными процентами по учетной ставке:
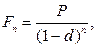 (76)
(76)
где n – число периодов начисления сложных процентов.
· Формула наращения сложными процентами по учетной ставке при начислении процентов несколько раз в год:
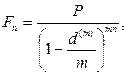 (77)
(77)
где n – число лет, m – количество начислений в год.
· Формула наращения непрерывными процентами:
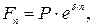 (78)
(78)
где δ – сила роста.
· Формула для определения срока ссуды (при непрерывном начислении процентов):
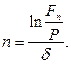 (79)
(79)
· Формула для определения силы роста:
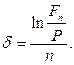 (80)
(80)
· Эквивалентность простых и сложных ставок:
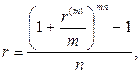 (81)
(81)
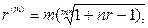 (82)
(82)
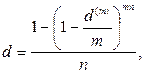 (83)
(83)
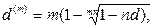 (84)
(84)
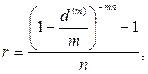 (85)
(85)
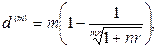 (86)
(86)
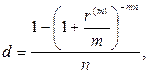 (87)
(87)
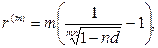 (88)
(88)
где r, d – простые ставки.
· Эквивалентность сложных ставок:
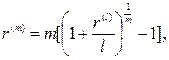 (89)
(89)
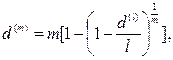 (90)
(90)
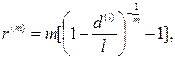 (91)
(91)
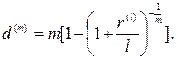 (92)
(92)
· Эквивалентность силы роста и простых ставок:
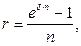 (93)
(93)
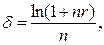 (94)
(94)
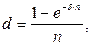 (95)
(95)
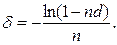 (96)
(96)
где r, d – простые ставки.
· Эквивалентность силы роста и сложных ставок:
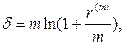 (97)
(97)
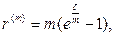 (98)
(98)
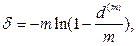 (99)
(99)
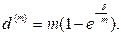 (100)
(100)
· Формулы наращения сложными процентами с учетом уплаты налога:
а) если налог на все полученные проценты выплачивается один раз в конце срока:
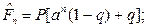 (101)
(101)
б) если налог на полученные проценты выплачивается каждый год:
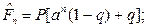 (102)
(102)
где q – ставка налога на проценты, a – коэффициент наращения, равный либо 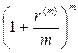 , либо
, либо 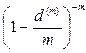 , либо
, либо 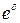 .
.
· Формулы для вычисления величины налога за каждый год при наращении сложными процентами, если налог на полученные процентами выплачивается каждый год:
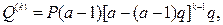 (103)
(103)
где k – номер года, за который взимается налог.
· Формула наращения сложными или непрерывными процентами с учетом инфляции:
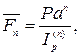 (104)
(104)
где Ip(n) – индекс инфляции за период n, a – равно либо 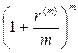 , либо
, либо 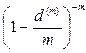 , либо
, либо 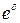 .
.
· Формула определения номинальной годовой процентной ставки, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной номинальной годовой ставке r(m):
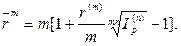 (105)
(105)
· Формула определения реальной номинальной годовой процентной ставки при объявленной исходной процентной ставке r(m) в условиях инфляции:
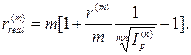 (106)
(106)
· Формула определения номинальной годовой учетной ставки, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной номинальной годовой ставке d(m):
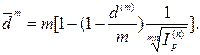 (107)
(107)
· Формула определения реальной номинальной годовой учетной ставки при объявленной исходной учетной ставке d(m) в условиях инфляции:
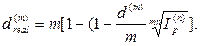
· Формула определения силы роста, обеспечивающей в условиях инфляции реальную доходность согласно первоначальной силе роста δ:
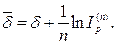 (109)
(109)
· Формула определения реальной силы роста при объявленной исходной силе роста δ в условиях инфляции:
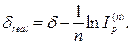 (110)
(110)
· Формула Фишера:
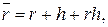 (111)
(111)
где h – годовой темп инфляции.
· Формула для вычисления величины нового платежа при использовании сложных ставок:
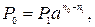 (112)
(112)
где P1 и n1 – первоначальный платеж и срок его выплаты, n0 – срок выплаты нового платежа, a – равно либо 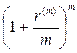 , либо
, либо 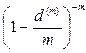 , либо
, либо 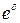 .
.
· Формула для вычисления срока нового платежа при использовании сложных ставок:
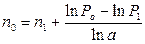 (113)
(113)
где P1 и n1 – первоначальный платеж и срок его выплаты, P0 – величина нового платежа.
· Формула для определения величины консолидированного платежа при использовании сложных ставок:
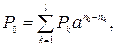 (114)
(114)
где P1, P2,…,Pl, ‑ платежи, выплачиваемые соответственно через время n1, n2,…, nl; n0 – срок консолидированного платежа.
· Формула для определения срока консолидированного платежа при использовании сложных ставок:
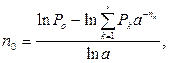 (115)
(115)
где платежи P1, P2,…,Pl, уплачиваемые соответственно через время n1, n2,…, nl; P0 – величина консолидированного платежа.
· Будущая стоимость переменного аннуитета постнумерандо:
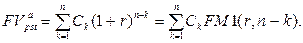 (116)
(116)
· Приведенная стоимость переменного аннуитета постнумерандо:
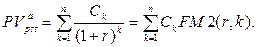 (117)
(117)
· Будущая стоимость переменного аннуитета пренумерандо:
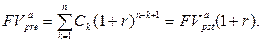 (118)
(118)
· Приведенная стоимость переменного аннуитета пренумерандо:
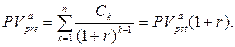 (119)
(119)
· Будущая стоимость постоянного срочного аннуитета постнумерандо:
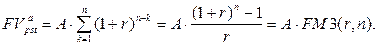 (120)
(120)
· Приведенная стоимость постоянного срочного аннуитета постнумерандо:
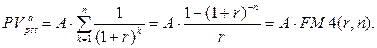 (121)
(121)
· Оценка постоянного p-срочного аннуитета постнумерандо:
а) будущая стоимость аннуитета: 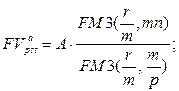 (122)
(122)
б) приведенная стоимость аннуитета: 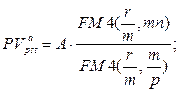 (123)
(123)
в) приведенная стоимость бессрочного аннуитета:
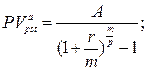 (124)
(124)
где A – величина каждого денежного поступления, r – ставка за базовый период начисления процентов, m – количество начислений сложных процентов в периоде, p – количество денежных поступлений в периоде, n – количество периодов.
· Приведенная стоимость постоянного отсроченного аннуитета постнумерандо:
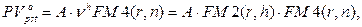 (125)
(125)
где 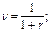 h – число периодов, через которое начинает поступать первый из потока платежей.
h – число периодов, через которое начинает поступать первый из потока платежей.
· Оценка постоянного p-срочного аннуитета пренумерандо:
а) будущая стоимость аннуитета:
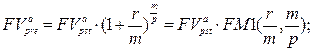 (126)
(126)
б) приведенная стоимость аннуитета:
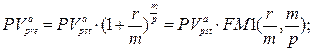 (127)
(127)
в) приведенная стоимость бессрочного аннуитета:
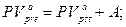 (128)
(128)
где 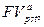
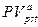 ‑ будущая и приведенная стоимости соответствующих аннуитетов постнумерандо.
‑ будущая и приведенная стоимости соответствующих аннуитетов постнумерандо.
· Будущая стоимость постоянного p-срочного аннуитета постнумерандо с начислением простых процентов в течение периода:
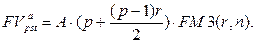 (129)
(129)
· Будущая стоимость постоянного p-срочного аннуитета пренумерандо с начислением простых процентов в течение периода:
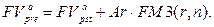 (130)
(130)
· Оценка постоянного аннуитета постнумерандо в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета: 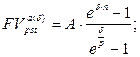 (131)
(131)
б) приведенная стоимость аннуитета: 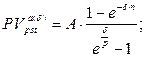 (132)
(132)
в) приведенная стоимость бессрочного аннуитета:
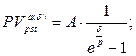 (133)
(133)
где A – величина каждого денежного поступления, δ– сила роста за базовый период начисления процентов, p – количество денежных поступлений в периоде, n – количество периодов.
· Оценка непрерывного аннуитета:
а) будущая стоимость аннуитета:
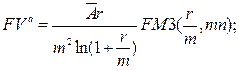 (134)
(134)
б) приведенная стоимость аннуитета:
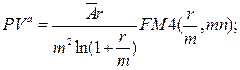 (135)
(135)
в) приведенная стоимость бессрочного аннуитета:
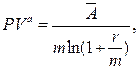 (136)
(136)
где 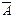 – суммарная величина денежных поступлений за базовый период начисления процентов.
– суммарная величина денежных поступлений за базовый период начисления процентов.
· Оценка непрерывного аннуитета в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета:
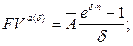 (137)
(137)
б) приведенная стоимость аннуитета:
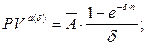 (138)
(138)
в) приведенная стоимость бессрочного аннуитета:
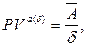 (139)
(139)
где 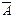 – суммарная величина денежных поступлений за базовый период начисления процентов, δ– сила роста за базовый период начисления процентов.
– суммарная величина денежных поступлений за базовый период начисления процентов, δ– сила роста за базовый период начисления процентов.
· Оценка переменного аннуитета постнумерандо, платежи которого образуют арифметическую прогрессию:
а) будущая стоимость аннуитета:
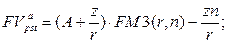 (140)
(140)
б) приведенная стоимость аннуитета:
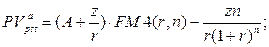 (141)
(141)
в) приведенная стоимость бессрочного аннуитета:
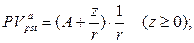 (142)
(142)
где A – первый член прогрессии, z – разность прогрессии.
· Оценка переменного аннуитета постнумерандо, платежи которого образуют геометрическую прогрессию:
а) будущая стоимость аннуитета:
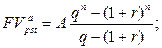 (143)
(143)
б) приведенная стоимость аннуитета:
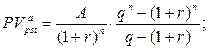 (144)
(144)
в) приведенная стоимость бессрочного аннуитета:
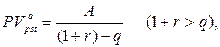 (145)
(145)
где A – первый член прогрессии, q – знаменатель прогрессии.
· Оценка постоянного аннуитета постнумерандо, период которого больше базового периода начисления процентов:
а) будущая стоимость аннуитета: 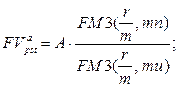 (146)
(146)
б) приведенная стоимость аннуитета:
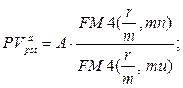 (147)
(147)
в) приведенная стоимость бессрочного аннуитета:
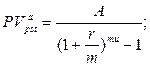 (148)
(148)
где A – величина каждого денежного поступления, r – ставка за базовый период начисления процентов, m – количество начислений сложных процентов в периоде, u – количество периодов, через которое осуществляются денежные поступления, n – количество периодов.
· Оценка постоянного аннуитета постнумерандо, период которого больше базового периода начисления процентов, в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета:
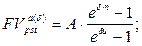 (149)
(149)
б) приведенная стоимость аннуитета:
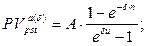 (150)
(150)
в) приведенная стоимость бессрочного аннуитета:
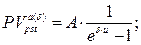 (151)
(151)
где A – величина каждого денежного поступления, δ– сила роста за базовый период начисления процентов, u – количество периодов, через которое осуществляются денежные поступления, n – количество периодов.
· Оценка постоянного аннуитета пренумерандо, период которого больше базового периода начисления процентов:
а) будущая стоимость аннуитета:
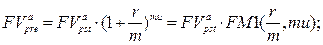 (152)
(152)
б) приведенная стоимость аннуитета:
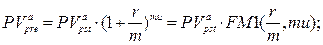 (153)
(153)
· Оценка постоянного аннуитета пренумерандо, период которого больше базового периода начисления процентов, в случае начисления непрерывных процентов:
а) будущая стоимость аннуитета: 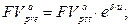 (154)
(154)
б) приведенная стоимость аннуитета: 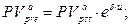 (155)
(155)
Приложение 2
