Начисление процентов по сложной годовой процентной ставке

В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, для наращения применяют сложные проценты. База для начисления сложных процентов (в отличие от простых) не остается постоянной – она увеличивается с каждым шагом во времени, абсолютная сумма начисленных процентов возрастает и процесс увеличения суммы долга происходит с ускорением. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называют капитализацией процентов.

Формула наращения годовых сложных процентов (проценты начисляются и капитализируются один раз в году) имеет следующий вид:

S (T) = S (o) (1 + i)^T (4)

Проценты за этот же период равны:

I = S (T) – S (o) = S (o) [(1 + i)^T - 1].

Величину (1 + i)^T называют множителем наращения по сложным процентам. Значения этого множителя для целых чисел Т приводятся в таблицах сложных процентов.

Иногда в расчетах используются переменные ставки сложных процентов за отдельные периоды времени. В этом случае множитель наращения имеет следующий вид: (1 + i₁)ⁿ 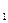(1 + i₂)ⁿ 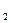… (1 + i_k)ⁿ ,

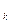где i₁, i₂, … , i_k – последовательные во времени значения ставок;

n₁, n₂, … , n_k – периоды, в течение которых действуют соответствующие ставки.

Обозначим q_m – процентную ставку для которой срок начисления меньше года и за год начисление процентов происходит m раз. Тогда наращенная сумма определяется по формуле S(T) = S(o) (1 + q_m). Например, месячная ставка равна 3%, тогда за год множитель наращения составляет (1 + 0,03)¹² = 1,43, т.е. первоначальный капитал увеличится в 1,43 раза.

Зная годовую процентную ставку можно определить ставку процентов за месяц, квартал и т.д. Например, годовая ставка сложных процентов равна 60%. Для того, чтобы определить месячную ставку iмес. приравняем множители наращения:

(1 + iмес)¹² = (1 + 0,6).

Из данного равенства найдем iмес. = (1,6)^1/12 – 1 = 4%. Ставка процентов за квартал составляет iкв. = (1,6)^1/4 – 1 = 12,5%. Процентная ставка за полугодие равна (1,6)^1/2 – 1 = 26,5%.

Если срок финансовой операции Т – не является целым числом, то возможен смешанный метод расчета наращенной суммы. В соответствии с ним начисление процентов за целое число лет идет по формуле сложных процентов, а за дробную часть периода по формуле простых процентов:

S (T) = S (o) (1 + i)^[T] (1 + i {T}),

где [T] – целая часть Т; {T} – дробная часть Т.

Пример 7.

Первоначальная сумма долга равна 50000000 руб. Определить наращенную сумму через 2,5 года, если используется ставка сложных процентов 25% годовых.

Решение:

Используя формулу (4) имеем:

S (T) = 50000000 (1 + 0,25)^2,5 = 87346390 (руб.)

Смешанный метод расчетов дает другой результат:

S (T) = 50000000 (1 + 0,25)² (1 + 0,25 × 0,5) = 87890625 (руб.).