Единовременные нетто-ставки по пожизненному страхованию на случай смерти

Для корректного расчета нетто-ставок необходимо правильно составить таблицу смертности и рассчитать коммутационные числа, на основе которых рассчитываются ставки.

Единовременные ставки по пожизненному страхованию на случай смерти рассчитывается на основе формул:

2.2.1. 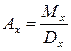– единовременная нетто-ставка при заключении пожизненного договора страхования на случай смерти для лица возраста х, выплаты страхового обеспечения производятся в конце года смерти.

Основным фактором, воздействующим на этот вид ставок, является фактор изменения процентной ставки: при уменьшении процентной ставки наблюдается увеличение тарифа, а при увеличении процентной ставки уменьшение тарифа.

содержание

Периодические нетто-ставки по пожизненному страхованию на случай смерти

Для корректного расчета нетто-ставок необходимо правильно составить таблицу смертности и рассчитать коммутационные числа, на основе которых рассчитываются ставки.

В общем случае для определения рассроченной нетто-ставки необходимо найти частное от деления единовременной нетто-ставки на соответствующий аннуитет. Нам потребуется формула аннуитета 1.1. для определения ежегодной нетто-ставки.

1.1. 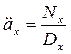– немедленный пожизненный аннуитет пренумерандо – ожидаемая стоимость взносов при пожизненном страховании, приведённая на начало действия договора страхования.

Наиболее часто используемая рассроченная ставка – ежегодная.

2.2.2. 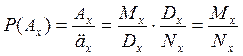– ежегодная нетто-ставка при заключении пожизненного договора страхования на случай смерти для лица возраста х, выплаты страхового обеспечения производятся в конце года смерти.

Фактор рассрочки позволяет сэкономить на персональном взносе, но через несколько лет (6-9 лет) становится фактором удорожания.

содержание

Коммутационные числа

Для упрощения расчетов тарифных ставок и резервов в контрактах по СЖ вводятся упрощающие функции – КОММУТАЦИОННЫЕ функции.

Все эти функции делятся на 2 группы:

- для доживающих

-для умерших.

Обязательным эл-том явл дисконтный мн-ль: .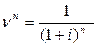

Основные коммутационные функции: (см вопрос 20)

1. Дисконтированные числа доживающих до возраста Х: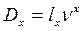

2. Сумма дисконтированных чисел всех доживающих и переживающих возраст х лет: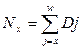

3. Сумма чисел: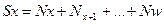

4. Дисконтированные числа умирающих в возрасте х лет: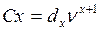

5. Сумма дисконтированных чисел умирающих в возрасте х лет и выше: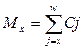

6.

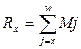
Dx, Nx, Sx выбраны для обозначения тк в простейших формулах страхования числа Dx играют роль знаменателя, числа Nx – числителя, а Sx-сумма Nx.

Сx, Mx, Rx – ближайшие по алфавиту.

Коммутационная функция строится из заданной ТС и при зажанной %-ой ставке.

Коммутац функции играли большую роль в докомпьютерную эпоху, тк значительно сокращали объем вычислений.

Западные актуарии доказали, что исп-ие коммутац функций приводит к несколько завышенным тарифам (около 1%).

Коммутац функции – технические показатели, не имеющие содержательного смысла.

Они лишь опред образом связывают показатели ТС и дисконтирующие мн-ли.

Что бы перевести в комутацион числа логические формулы (те, что записываются через интегралы) для расчета единоврем нетто-ставки:

1. записывается общая формула

2. числитель и знаменатель домножается на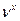

3. Это выражение записывается через коммутац числа.

содержание

30. Расчёт резервов по страхованию жизни.

Ответ из Касимова:

Существуют 2 метода расчета резервов в страховании жизни:

Метод расчета резервов, исходя из полученных премий за вычетом уплаченных страховых сумм, называется ретроспективным методом, поскольку он основывается на уже полученных премиях и выплаченных страховых суммах. Существует еще один метод, называемый проспективным, основанный на учете будущих поступлений и выплат. Конечно, оба метода дают одно и то же значение, если речь идет о чистых премиях. Проспективный метод основан на об­щем определении резерва как разности между текущими стоимостями будущих выплат и будущих премий.

Обозначим символом _t V_x величину конечных резервов для пожизненно­го страхования единичной суммы в конце t-го года после продажи полиса.

В конце t-го года текущее значение предстоящих выплат есть, очевид­но, А_х+1. Соответственно текущая стоимость ежегодных премий по этому контракту есть Р_х • 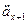Следовательно, согласно определению проспек­тивного резерва получаем

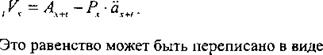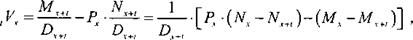Замечание. Следует отчетливо понимать, что, говоря о текущей сто­имости, мы имеем в виду год оценки резерва, т.е. t лет спустя после заклю­чения контракта.

При вычислении по ретроспективному методу мы в качестве оценки резервов должны рассмотреть разницу между полученными премиями и уже выплаченными страховыми суммами. Если х — возраст заключения контракта, a t — число лет после его заключения, то оценка резервов отно­сится к возрасту x + t - Если Р_х — величина ежегодной премии, текущая стоимость к моменту заключения контракта всех премиальных взносов за t лет для / застрахованных составит

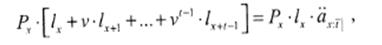
а текущая стоимость всех выплат (единичной суммы!) —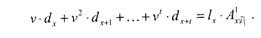

Таким образом, мы доказали, что вычисления резервов по обоим мето­дам дает одинаковый результат для контрактов страхования жизни. Резервы, рассчитанные по проспективному методу, представлены ниже:

содержание