Дюрация как средний срок платежей
Дюрация.
При расчете доходности к погашению неявно предполагалось, что все денежные поступления в каждый период вновь кладутся (реинвестируются) в банк под проценты на оставшееся до погашения время. Но через время процентная ставка может измениться.
Таким образом, возникает как риск реинвестирования, так и риск при продаже ценной бумаги до срока погашения. Поэтому возникла потребность просчитывать риск изменения процентных ставок, приводящий как к обесценению активов, так и к возможности непокрытия имеющихся долгов. В результате возникают задачи контролирования процентного риска для получения безрисковой доходности на вложенный капитал, а также задачи, целью которых является гарантия погашения обязательств.
Одним из способов решения подобных задач является формирование такого пакета облигаций, который, обладая требуемыми свойствами, сохраняет их независимо от изменения доходности на рынке.
Допустим принадлежащий инвестору пакет облигаций производит финансовый поток {CT, 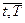 }, с текущей стоимостью Р и обязательной календарной выплатой РК.
}, с текущей стоимостью Р и обязательной календарной выплатой РК.
Напомним:
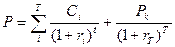 (8.1)
(8.1)
Приведенная величина этого потока Р зависит от процентных ставок rt, поэтому их вероятностные изменения могут неблагоприятно сказаться на ее величине и могут также привести к возможности неуплаты долга.
Для простоты будем предполагать, что все доходности одинаковы во времени.
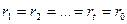 (8.2)
(8.2)
И если в ставке 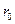 происходят какие-то изменения, то они происходят в самом начале.
происходят какие-то изменения, то они происходят в самом начале.
Одной из причин изменения процентной ставки является изменение денежного рынка. Так уменьшение денежной массы приводит к неудовлетворенному спросу на деньги. Вследствие этого банки повысят ставку до r > r0. При избытке денег банки снижают процентную ставку, и r станет меньше r0.
Дюрация как мера чувствительности.
Имеется функция y=f(x).
Коэффициент чувствительности (эластичности) показывает, на сколько процентов изменится функция y при изменении относительной величины аргумента x на 1 процент.
Коэффициент эластичности определяется выражением:
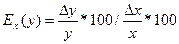 (3)
(3)
Откуда получаем:
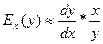 (4)
(4)
Текущая стоимость денежного потока имеет вид:
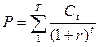 (5)
(5)
В итоге, коэффициент чувствительности текущей стоимости Р на изменение процентной ставки r будет равен:
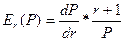 (6)
(6)
Находим производную Р по r:
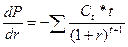 (7)
(7)
Подставив (7) в (6) получаем коэффициент эластичности:
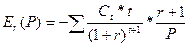 (8)
(8)
Из выражения (3) получаем:
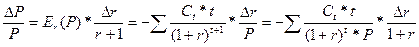 (9)
(9)
Обозначим:
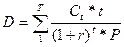 (10)
(10)
Это выражение называется дюрацией. Размерность дюрации — год.
Подставив (10) в выражение (9) получаем:
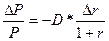 (11)
(11)
Таким образом, дюрация есть коэффициент чувствительности между относительным изменением наращивания и относительным изменением текущей стоимости.
Пример 1:
Имеется облигация номиналом 1000 д.е., купон 5%. Срок погашения 3 года; безрисковая (банковская) ставка 10%. Определить, на сколько уменьшится текущая стоимость облигации при увеличении банковской ставки до 12%.
Решение:
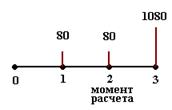
Данная облигация образует денежный поток. Изобразим его на рисунке.
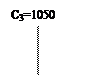 |
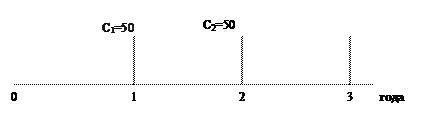
Текущая стоимость данного потока будет:
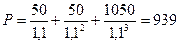 д.е.
д.е.
Дюрация данного денежного потока будет:
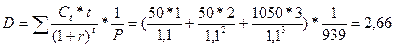 года
года
Определим, на сколько изменится относительная текущая стоимость облигации.
Согласно выражению (11) (для 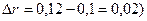 имеем:
имеем:
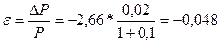
В результате текущая стоимость уменьшилась на 4,8%.
Новое значение текущей стоимости облигации стало:
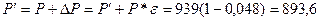 д.е.
д.е.
Текущая стоимость при увеличении банковской ставки на 2% уменьшилась на 45,4 д.е.
Дюрация как средний срок платежей.
Итак, мы определили дюрацию как чувствительность относительного изменения текущей стоимости к относительному изменению наращивания (1+r).

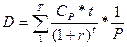
Обозначим:
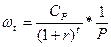 , которая имеет смысл псевдовероятности, поскольку:
, которая имеет смысл псевдовероятности, поскольку:
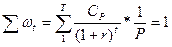 , (т.к.
, (т.к. 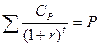 )
)
Сопоставим потоку платежей {CT, 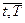 } искусственную случайную величину Q, равную дате платежа: ее возможные значения соответствуют последовательным моментам датированных выплат. Таким образом, Q принимает целочисленные значения от 1 до Т.
} искусственную случайную величину Q, равную дате платежа: ее возможные значения соответствуют последовательным моментам датированных выплат. Таким образом, Q принимает целочисленные значения от 1 до Т.
Вероятность каждого из этих значений определим той долей 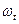 , которую вносит отдельный платеж Сt в текущую стоимость Р всего потока платежей.
, которую вносит отдельный платеж Сt в текущую стоимость Р всего потока платежей.
Представим обобщенную характеристику потока платежей {Ct}, соответствующую псевдослучайной величине Q, следующим рядом распределения:
| Величина Q | … | t | … | T | ||
Вероятность 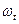 | 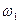 | 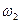 | … | 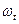 | … | 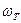 |
Найдем мат. ожидание и дисперсию этой случайной величины.
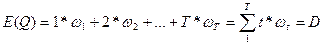
Таким образом, дюрацию можно интерпретировать как среднюю длительность платежей в потоке.
Дисперсия случайной величины определяем выражением:
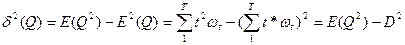
Пример 2:
Рассмотрим два потока платежей A и B с перераспределением денежных поступлений на начало и конец отчетного периода.
А = (1600, 400, 100); В = (100, 400, 1600)
Пусть (для простоты) r = 0. Найти дюрации денежных потоков.
Решение:
Получаем текущие стоимости:

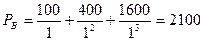
Для каждого потока имеем следующие ряды распределения:
| Величина Q(A) | |||
Вероятность 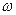 (A) (A) | 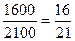 | 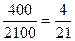 | 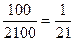 |
| Величина Q(B) | |||
Вероятность 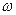 (B) (B) | 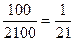 | 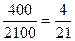 | 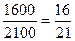 |
Отсюда найдем дюрацию (или среднюю срочность платежей) по каждому из потоков.
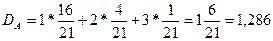 года
года
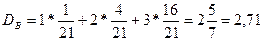 года
года
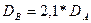
Отсюда следует, что для потоков с одинаковыми текущими стоимостями и выплатами, преобладание более ранних больших платежей уменьшает дюрацию, в то время как большие последующие выплаты ведут к ее росту.
Определим дисперсии для потоков А и В.
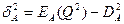
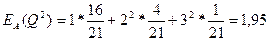 год2
год2
 год2
год2
Дисперсия для потока В:
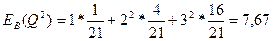
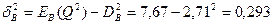
Как видим, дисперсии потоков А и В равны.
Отметим, что дюрация бескупонной облигации равна сроку ее погашения.
Выпуклость
Пусть имеется функция 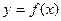 . Разложим ее в ряд Тейлора в окрестности точки x0:
. Разложим ее в ряд Тейлора в окрестности точки x0:
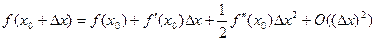 (13)
(13)
p(текущая стоимость) является функцией; r – банковская ставка – аргументом. Приращение текущей стоимости согласно (13) имеет вид:
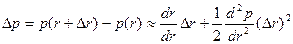 (14)
(14)
Разделим обе части (14) на p. Получаем:
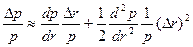 (15)
(15)
Согласно выражениям (7),(8),(9) первое слагаемое правой части выражения (15) можно представить в виде:
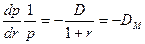 (16),
(16),
где 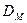 - модифицированная дюрация.
- модифицированная дюрация.
Сочетание 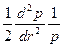 называется выпуклостью и обозначается:
называется выпуклостью и обозначается:
Convex = 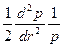 (17)
(17)
Определим вторую производную текущей стоимости от банковской ставки. Для этого продифференцируем выражение (7) по r. Получаем:
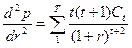 (18)
(18)
Подставив (18) в (17) получаем формулу выпуклости:
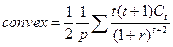 (19)
(19)
В результате получаем:
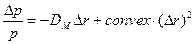 (20)
(20)
Размерность convex (год2)
Проиллюстрируем выражение (14) рисунком: зависимость текущей стоимости облигации от процентной ставки r имеет вид кривой:
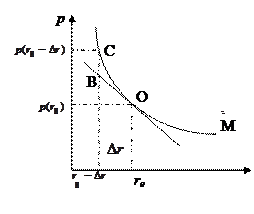
A
|
Приращение текущей стоимости 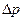 состоит из двух отрезков АВ, которые определяются выражением
состоит из двух отрезков АВ, которые определяются выражением  и ВС, который определяется выражением
и ВС, который определяется выражением 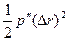 , и учитывает выпуклость.
, и учитывает выпуклость.
Отметим, что при значительных изменениях процентной ставки нужно пользоваться более точной формулой (20).
Пример 2:
Пусть процентная ставка в условиях примера 1 увеличилась на 5% (вместо 2%). В этом случае относительное изменение текущей стоимости будем определять не выражением (11), а формулой (20). Согласно формуле (19) выпуклость будет:
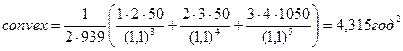
Модифицированная дюрация:
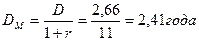
Подставив эти значения в выражение (20), получаем:
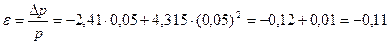
Изменение текущей стоимости:
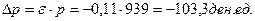
Новая курсовая стоимость облигации:
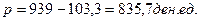
Покрытие долга.
Актив впереди долга.
Вам необходимо выплатить долг в размере L в момент времени t2. Для этого вы покупаете в текущей момент (t=0) облигацию номиналом А, которая определяется условием:
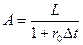 ,
,
где 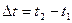 ;
; 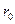 - банковская процентная ставка,
- банковская процентная ставка, 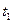 - срок погашения.
- срок погашения.
Изобразим это на рисунке:

Если процентная ставка за промежуток от 0 до t1, не изменится, то получв в момент t1, номинал А и, положив деньги в банк по ставке r0, получаем:
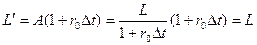
Как видим, долг покрывается.
Однако, если процентная ставка за 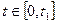 уменьшится до величины r1<r0, то получив номинал А и положив его в банк по ставке r1, получаем:
уменьшится до величины r1<r0, то получив номинал А и положив его в банк по ставке r1, получаем:
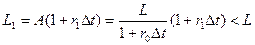
Таким образом, долг не будет покрыт.
Следовательно, если покрытие долга осуществляется облигацией, срок погашения которой меньше срока возврата долга (актив впереди долга), то при уменьшении процентной ставки долг не покрывается, и наоборот, увеличение процентной ставки перекрывает долг.
Долг впереди актива.
Вам необходимо отдать долг L, в момент t1. Для этого в момент 0 покупается облигация номиналом А со сроком исполнения t2>t1. Подбираем номинал А так, чтобы текущая стоимость в момент t1 равнялась долгу L.
Изобразим эту схему на рисунке:
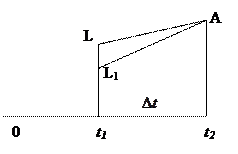
Величина номинала равна:
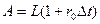
Если процентная ставка не изменится, то стоимость облигаций в момент t1 ,будет:
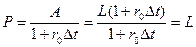
Долг покрывается. Однако, если ставка увеличится (r1>r0), то стоимость облигации в момент t1 будет:
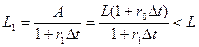
Долг не покрывается.
Таким образом, если долг впереди актива, то при увеличении процентной ставки не покрывает долг. И наоборот, при уменьшении процентной ставки долг покрывается.
Иммунизация
Понятие дюрации привело к развитию техники управления пакетами облигаций. Управляя пакетами облигаций, можно получить фиксированный доход независимо от риска изменения процентной ставки.
 | |||||
 | |||||
 | |||||
Рис.1 Кривые ПП и АА – графики текущих стоимостей потоков пассивов и активов, изображенные в осях «доходность – цена». Для базовой процентной ставки r0 в каждом рассматриваемом варианте а), б) и в) текущая стоимость актива равна текущей стоимости пассива (долга). РА=PB=P0.
Поэтому, если процентная ставка сохранится (r=r0), то для покрытия долга можно использовать любой из выделенных активов.
Однако, если процентная ставка не сохранится, то в случае а) разница в текущих стоимостях
PA-PП 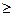 0. Это случай полного хеджирования.
0. Это случай полного хеджирования.
В случае б) 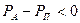 , но разница незначительна, случай b на кривой АА, при
, но разница незначительна, случай b на кривой АА, при 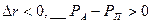 , но при
, но при 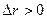 имеется риск непокрытия долга. При этом дефицит платежа (
имеется риск непокрытия долга. При этом дефицит платежа ( 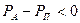 ) может быть значительным. В этом случае хеджирования нет.
) может быть значительным. В этом случае хеджирования нет.
Из рисунков видно, что необходимым условием хеджирования является касание кривых автива и пассива в точке (r0, Р0) или:
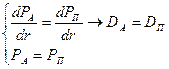
Другими словами, при хеджировании должны быть равны текущая стоимость активов и пассивов и их дюрации.
При этом, в случае полного хеджирования, выпуклость актива должна быть больше выпуклости пассива.
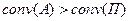
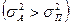 .
.
Если хеджирование неполное, наоборот.
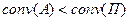
Хеджирование вклада.
Иммунизация позволяет составить портфель из облигаций, который может хеджировать вклад от процентного риска.
Пример.Имеется два типа облигаций: тип А - номинал 1000 д.е., купон 80 д.е., срок погашения 3 года; и тип В – номинал 1000 д.е., купон 70 д.е., срок погашения 1 год.
Предназначенный для вклада капитал составляет 10500 д.е. определить, в каком количестве нужно купить облигации этих типов, чтобы обезопасить вклад от процентного риска. Банковская ставка составляет 10%. Деньги вкладываются на 2 года.
Решение.
Текущая стоимость портфеля:
V = VА + VB (1)
Где VА – часть вклада вносимая облигациями типа А
VВ – часть вклада вносимая облигациями типа В.
Доли вклада:
wА = VА / V , wв = Vв / V - доли вклада,
wА + wв = 1 (2)
Дюрация портфеля (актива) определяется выражением:
D = DАwА + DВwВ (3)
Эта дюрация равна сроку вклада (дюрация пассива).
Текущая стоимость облигации А:
РАТ = 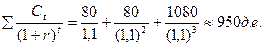
Дюрация облигации А:
Da= 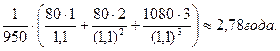
Текущая стоимость облигации В:
РвТ = 1070/1,1 = 973
Дюрация облигации В:
Dв = 1.
В результате имеем систему:
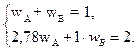
Откуда wА =0,56, wв = 0,44.
Часть капитала, предназначенная на покупку облигаций А:
VА = wА* V = 10500*0,56 = 5880
VB = wB V= 10500 0,44 = 4620
На сумма вклада VА = 5880 нужно купить по текущей стоимости 950 д.е. количество облигаций, равное nA = VA/PAT = 5880/950 = 6,189 = 6 шт.
На сумму VB = 4620 нужно купить по текущей стоимости 973 д.е. количество облигаций, равное nВ = VВ/PВT = 4620/973 = 4,74 = 5 шт.
Покажем, что созданный портфель хеджирует вклад от процентного риска.
Если бы вклад положили в банк по 10% ставке, что через 2 года получили бы сумму:
V=10500*(1,1)2 = 12705.
Однако, если ставка понизится до 5%, то накопленная сумма составит
V`=10500*(1,05)2 =11576,2 д.е.
В результате вкладчик потеряет 1128, 75 д.е. вследствие процентного риска. (12705-11576,2=1128,75).
Этого не случится, если вкладчик купит облигации в указанном количестве и применит алгоритм хеджирования.
Тогда на сумму V = 10500 покупаем облигации типов А и В в количестве nA = 6,189, nB = 4,74.
Рассмотрим финансовый результат к концу 2-ого года по облигация А и В.
По облигациям А:
Пусть процентная ставка уменьшится до 5% после покупки облигаций. Тогда за 1-ый год получим купоны 80 д.е. и эти деньги положим в банк под 5%. К концу 2-ого года стало С1(1+r) = 80(1,05) = 84. в конце 2-ого года получаем второй купон 80 д.е. и продаем облигацию по текущей стоимости РА` = 1080/(1,05) = 1028,6.
В итоге по одной облигации А финансовый результат к концу 2-ого года РА`` = 80+84+1028,6 = 1192,6
По облигациям имеем:
VA = 6*1192,6 = 7155,6 д.е.
По облигациям В:
| |

По облигации типа В в конце 1-ого года получим наминал плюс купон 1070 д.е. На эти деньги покупаем новую облигацию по новой текущей стоимости:
РВ` = 1070/1,05 = 1019.
Разницу DРВ = 1070-1019 = 51 д.е. положим в банк по ставке 5% и получаем к концу 2-ого года DРВ`=51(1+0,05) = 53,552 г.
По новой облигации B к концу 2-го года получаем наминал плюс купон = 1070.
В итоге сумма по облигации В будет 1070+53,55=1123,55
По пяти облигациям получаем: VВ=1123,55*5=5617,75.
Итоговая сумма в момент времени Т=2 будет равна выручке от продаже всех облигаций:
V = VА + VB = 7155,6+5617,75 = 12773,3, что больше суммы по депозиту, равной 12705, на 68,3 д.е.
