Задача замены оборудования
Чем дольше механизм эксплуатируется, тем выше затраты на его обслуживание и ниже его производительность. Когда срок эксплуатации механизма достигает определенного уровня, может оказаться более выгодной его замена. Задача замены оборудования, таким образом, сводится к определению оптимального срока эксплуатации механизма.
Предположим, что мы занимаемся заменой механизмов на протяжении n лет. В нчале каждого года принимается решение либо об эксплуатации механизма еще один год, либо о замене его новым. Обозначим через 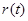 и
и 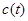 и прибыль от эксплуатации
и прибыль от эксплуатации 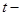 летнего механизма на протяжении года и затраты на его обслуживание за этот же период. Далее пусть s(t) — стоимость продажи механизма, который эксплуатировался t лет. Стоимость приобретения нового механизма остается неизменной на протяжении всех лет и равна I. Элементы модели динамического программирования таковы.
летнего механизма на протяжении года и затраты на его обслуживание за этот же период. Далее пусть s(t) — стоимость продажи механизма, который эксплуатировался t лет. Стоимость приобретения нового механизма остается неизменной на протяжении всех лет и равна I. Элементы модели динамического программирования таковы.
1. Этап i представляется порядковым номером года i,i= 1,2,...,п.
2. Вариантами решения на i-м этапе (т.е. для i-го года) являются альтернативы: продолжить эксплуатацию или заменить механизм в начале i-го года.
3. Состоянием на i-м этапе является срок эксплуатации t (возраст) механизма к началу i-гo года.
Пусть 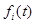 — максимальная прибыль, получаемая за годы от i до п при условии, что в начале i-го года имеется механизм t-летнего возраста.
— максимальная прибыль, получаемая за годы от i до п при условии, что в начале i-го года имеется механизм t-летнего возраста.
Рекуррентное уравнение имеет следующий вид.
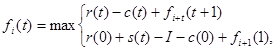
где 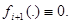
Пример 4-3
Компания планирует определить оптимальную политику замены имеющегося в настоящее время трехлетнего механизма на протяжении следующих 4 лет (n=4), т.е. вплоть до начала пятого года. Приведенная таблица содержит относящиеся к задаче данные. Компания требует замены механизма, который в эксплуатации 6 лет. Стоимость нового механизма равна 100000 долларов.
Возраст  (года) (года) | Прибыль  ($) ($) | Стоимость обслуживания 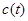 ($) ($) | Остаточная стоимость s(t) ($) |
| – | |||
Определение допустимых значений возраста механизма на каждом этапе является нетривиальной задачей. На рис 4 представлена рассматриваемая задача замены оборудования в виде сети. В начале первого года имеется механизм трехлетнего возраста. Мы можем либо заменить его (3), либо эксплуатировать (С) на протяжении следующего года. Если механизм заменили, то в начале второго года его возраст будет равен одному году, в противном случае его возраст будет 4 года. Такой же подход используется в начале каждого года, начиная со второго по четвертый.
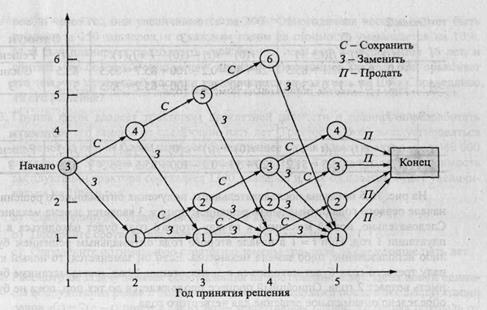 |
Если однолетний механизм заменяется в начале второго или третьего года, то заменивший его механизм к началу следующего года также будет однолетним. К тому же, в начале 4-го года 6-летний механизм обязательно должен быть заменен, если он еще эксплуатируется; в конце 4-го года все механизмы продаются (П) в обязательном порядке. На схеме сети также видно, что в начале второго года возможны только механизмы со сроком эксплуатации 1 или 4 года. В начале третьего года механизм может иметь возраст 1, 2 или 5 лет, а в начале четвертого — 1,2,3 или 6 лет.
Решение данной задачи эквивалентно нахождению маршрута максимальной длины (т.е. приносящего максимальную прибыль) от начала первого года к концу четвертого в сети, показанной на рис. 4. При решении этой задачи используем табличную форму записи. (Числовые Данные в таблице кратны тысячам долларов.).
| Этап 4. | ||||
| t | C | З | Оптимум | |
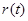 +s(t+1)- +s(t+1)- 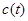 | 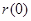 +s(t)+s(1)- +s(t)+s(1)- 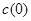 -I -I |  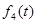 | Решение | |
| 19.0+60-0.6=78.4 | 20+80+80-0.2-100=79.8 | 79.8 | З | |
| 18.5+50-1.2=67.3 | 20+60+80-0.2-100=59.8 | 67.3 | С | |
| 17.2+30-1.5=45.7 | 20+50+80-0.2-100=49.8 | 49.8 | З | |
| Необходима замена | 20+5+80-0.2-100=4.8 | 4.8 | З | |
| Этап 3. | ||||
| t | C | З | Оптимум | |
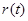 - - 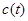 + + 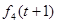 | 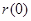 +s(t)- +s(t)- 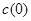 -I+ -I+ 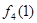 |  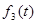 | Решение | |
| 19.0-0.6+67.3=85.7 | 20+80-0.2-100+79.8=79.6 | 85.7 | С | |
| 18.5-1.2+49.8=67.1 | 20+60-0.2-100+79.8=59.6 | 67.1 | С | |
| 14.0+1.8-4.8=17.0 | 20+10-0.2-100+79.8=9.6 | 17.0 | С | |
| Этап 2. | ||||
| t | C | З | Оптимум | |
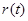 - - 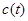 + + 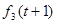 | 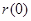 +s(t)- +s(t)- 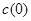 -I+ -I+ 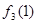 |  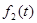 | Решение | |
| 19.0-0.6+67.1=85.5 | 20+80-0.2-100+85.7=85.5 | 85.5 | С или З | |
| 19.0-0.6+67.3=85.7 | 20+80-0.2-100+79.8=79.6 | 85.7 | З | |
| Этап 2. | ||||
| T | C | З | Оптимум | |
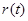 - - 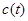 + + 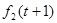 | 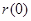 +s(t)- +s(t)- 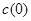 -I+ -I+ 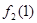 |  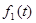 | Решение | |
| 17.2-1.5+35.5=51.2 | 20+50-0.2-100+85.5=55.3 | 55.3 | З |
На рис. 5 показана последовательность получения оптимального решения. В начале первого года оптимальным решением при t = 3 является замена механизма. Следовательно, новый механизм к началу второго года будет находиться в эксплуатации 1 год. При t = 1 в начале второго года оптимальным решением будет либо использование, либо замена механизма. Если он заменяется, то новый к началу третьего года будет находиться в эксплуатации 1 год, иначе механизм будет иметь возраст 2 года. Описанный процесс продолжается до тех пор, пока не будет определено оптимальное решение для четвертого года.
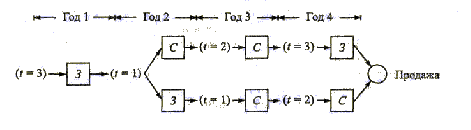
Следовательно, начиная с первого года эксплуатации механизма, альтернативными оптимальными стратегиями относительно замены механизма будут (3, С, С, 3) и (3, 3, С, С). Общая прибыль составит 55 300 долларов.
Упражнения 4.4,с
1. Постройте сеть и найдите оптимальное решение в задаче из примера 4-3 в каждом из следующих случаев.
a) В начале первого года имеется механизм, находящийся в эксплуатации 2 года.
b) В начале первого года имеется механизм, находящийся в эксплуатации 1 год.
c) В начале первого года куплен новый механизм.
2. Мой тринадцатилетний сын занимается собственным бизнесом — косит газоны десяти клиентам. Каждому клиенту он косит траву три раза в год, получая за один скошенный газон 50 долларов. Он купил косилку за 200 долларов. На протяжении первого года затраты на содержание и использование косилки равны 120 долларов, и через год они увеличиваются на 20%. Одногодичная косилка может быть продана за 150 долларов, и с каждым годом ее стоимость уменьшается на 10%. Мой сын планирует продолжить свой бизнес, пока ему не исполнится 16 лет, и считает, что более выгодно менять косилку через каждые два года. Он объясняет это тем, что цена новой косилки увеличивается за год лишь на 10%. Справедливо ли его решение?
3. Группа ферм владеет трактором двухлетней давности и планирует разработать стратегию его замены на следующие пять лет. Трактор должен эксплуатироваться не менее двух и не более пяти лет. В настоящее время новый трактор стоит 40 000 долларов, и эта цена за год увеличивается на 10%. Текущая годичная стоимость эксплуатации трактора составляет 1300 долларов и, как ожидается, будет увеличиваться на 10% в год.
a) Сформулируйте задачу в виде задачи о кратчайшем пути.
b) Постройте соответствующее рекуррентное уравнение.
c) Определите оптимальную стратегию замены трактора на следующие пять лет.
4. Рассмотрим задачу замены оборудования на протяжении п лет. Цена новой единицы оборудования равна с долларов, а стоимость продажи после t лет эксплуатации равна s(t)=2(n-t) при п>t и нулю — в противном случае. Годичная прибыль от эксплуатации является функцией возраста оборудования t и равна r(t)=r2-t2 при п>t и нулю — в противном случае.
a) Сформулируйте задачу как модель динамического программирования.
b) Определите оптимальную стратегию замены оборудования двухгодичной давности при с=10 000 долларов, считая, что п=5.
5. Решите задачу из предыдущего упражнения, предполагая, что возраст оборудования составляет 1 год и п = 4, с = 6000 долларов, r(t) = n/(n + 1).
Задача инвестирования
Предположим, что в начале каждого из следующих п лет необходимо сделать инвестиции p1, p2, ..., Рп соответственно. Вы имеете возможность вложить капитал в два банка: первый банк выплачивает годовой сложный процент r1, а второй— r2. Для поощрения депозитов оба банка выплачивают новым инвесторам премии в виде процента от вложенной суммы. Премиальные меняются от года к году, и для i-го года равны qi1 и qi2 в первом и втором банках соответственно. Они выплачиваются в конце года, на протяжении которого сделан вклад, и могут быть инвестированы в один из двух банков на следующий год. Это значит, что лишь указанные проценты и новые деньги могут быть инвестированы в один из двух банков. Размещенный в банке вклад должен находиться там до конца рассматриваемого периода. Необходимо разработать стратегию инвестиций на следующие п лет.
Элементы модели динамического программирования следующие.
1. Этап i представляется порядковым номером года i, i= 1,2,..., n.
2. Вариантами решения на i-м этапе (для i-го года) являются суммы 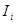 и
и 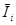 , инвестиций в первый и второй банк соответственно.
, инвестиций в первый и второй банк соответственно.
3. Состоянием хi на i-м этапе является сумма денег на начало i-го года, которые могут быть инвестированы.
Заметим, что по определению 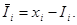 . Следовательно,
. Следовательно,
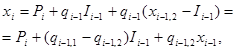
где 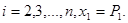 Сумма денег
Сумма денег 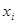 которые могут быть инвестированы, включает лишь новые деньги и премиальные проценты за инвестиции, сделанные на протяжении
которые могут быть инвестированы, включает лишь новые деньги и премиальные проценты за инвестиции, сделанные на протяжении 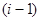 -го года.
-го года.
Пусть 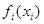 — оптимальная сумма инвестиций для интервала от
— оптимальная сумма инвестиций для интервала от 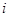 -го до n-го года при условии, что в начале
-го до n-го года при условии, что в начале 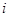 -го года имеется денежная сумма
-го года имеется денежная сумма 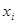 . Далее обозначим через
. Далее обозначим через  - накопленную сумму к концу п-гогода при условии, что
- накопленную сумму к концу п-гогода при условии, что 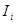 и (
и ( 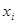 -
- 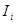 ) — объемы инвестиций на протяжении
) — объемы инвестиций на протяжении 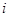 -го года в первый и второй банк соответственно. Обозначая
-го года в первый и второй банк соответственно. Обозначая 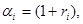 i = 1,2, мы можем сформулировать задачу в следующем виде.
i = 1,2, мы можем сформулировать задачу в следующем виде.
Максимизировать 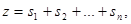
где
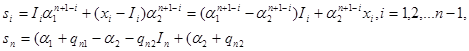
Так как премиальные за п-й год являются частью накопленной денежной суммы от инвестиций, в выражения для sn добавлены qn1 и qn2.
Итак, в данном случае рекуррентное уравнение для обратной прогонки в алгоритме динамического программирования имеет вид
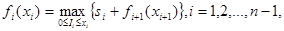
где хi+1 выражается через 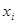 в соответствии с приведенной выше формулой, afn+1(xn+l)
в соответствии с приведенной выше формулой, afn+1(xn+l) 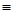 0.
0.
Пример 4-4
Предположим, вы хотите инвестировать 4000 долларов сейчас и 2000 долларов 3в начале каждого года, от второго до четвертого, считая от текущего года. Первый банк выплачивает годовой сложный процент 8% и премиальные на протяжении следующих четырех лет в размере 1.8%, 1.7%, 2.1% и 2.5% соответственно. Годовой сложный процент, предлагаемый вторым банком, на 0.2% ниже, чем предлагает первый банк, но его премиальные на 0.5% выше. Задача состоит в максимизации накопленного капитала к концу четвертого года.
Используя введенные выше обозначения, имеем следующее.

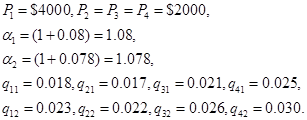
Этап 4.
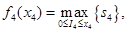
где 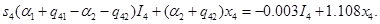
Функция 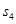 является линейной по I4 в области 0<I4<x4 и, следовательно, ее максимум достигается при I4=0 из-за отрицательного коэффициента при I4. Следовательно, оптимальное решение для этапа 4 может быть представлено в следующем виде.
является линейной по I4 в области 0<I4<x4 и, следовательно, ее максимум достигается при I4=0 из-за отрицательного коэффициента при I4. Следовательно, оптимальное решение для этапа 4 может быть представлено в следующем виде.
| Состояние | Оптимальное решение | |
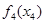 | I4* | |
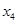 | 1.108х4 |
Этап 3.
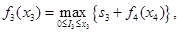
где
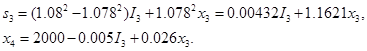
Следовательно,
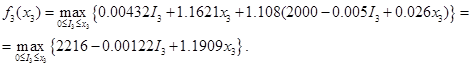
| Состояние | Оптимальное решение | |
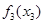 | I3* | |
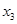 | 2216+1.1909х3 |
Этап 2.
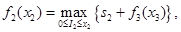
где
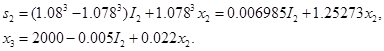
Следовательно,
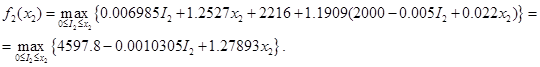
| Состояние | Оптимальное решение | |
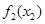 | I2* | |
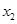 | 4597.8+1.27996х2 | x2 |
Этап 1.
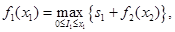
где
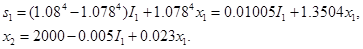
Следовательно,
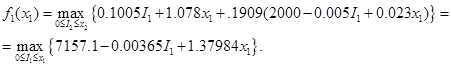
| Состояние | Оптимальное решение | |
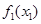 | I1* | |
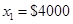 | 7157.7+1.3849х1 | $4000 |
При вычислениях в обратном направлении получаем следующее.
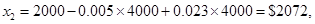
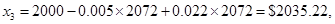
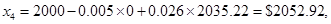
Следовательно, оптимальное решение будет записано следующим образом.
| Оптимальное решение | Решение, принимаемое инвестором |
I1*= 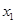 | Инвестировать 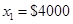 в первый банк в первый банк |
I2*= 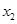 | Инвестировать 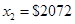 в первый банк в первый банк |
| I3*=0 | Инвестировать 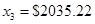 во второй банк во второй банк |
| I4*=0 | Инвестировать 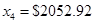 во второй банк во второй банк |

Упражнения 4.4, d
1. Решите задачу из примера 10.-4 в предложении, что 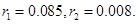 Кроме того, пусть
Кроме того, пусть 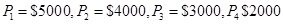 .
.
2. Некий инвестор с начальным капиталом в 10000 долларов должен решить в конце каждого года, сколько денег истратить и сколько инвестировать. Каждый инвестированный доллар возвращает 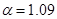 доллара в конце года приносят удовлетворение, определяемое количественно как эквивалент получения
доллара в конце года приносят удовлетворение, определяемое количественно как эквивалент получения 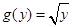 долларов. Решите задачу с помощью методов динамического программирования для периода в
долларов. Решите задачу с помощью методов динамического программирования для периода в 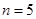 лет.
лет.
3. Фермер имеет k овец. В конце каждого года он принимает решение, сколько овец продать и сколько оставить. Прибыль от продажи одной овцы в i-й год равна pi. Количество овец в конце i-гoгода удваивается к концу (i+1)-го года. Фермер планирует в конце п-гогода полностью продать овец.
a) Получите общее рекуррентное уравнение для решения задачи.
c) Решите задачу при следующих данных: n=3 года, k=2овцы, p1=$100, р2 = $130, р3=$120.
d)
