Дисконтирующим множителем

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

___________________________________________________

ИНСТИТУТ ТЕХНОЛОГИЙ, ЭКОЛОГИИ И ПРЕДПРИНИМАТЕЛЬСТВА

_____________________________________________________________

Л.Н. Грошев

ФИНАНСОВАЯ МАТЕМАТИКА

Учебное пособие по курсу

«Финансовая математика»

для студентов, обучающихся по направлениям

«Экономика» и «Менеджмент»

Москва Издательство МЭИ 2005

65.9 (2)

Г - 899

ББК: 65.9 (2) 261.1

Утверждено учебным управлением МЭИ в качестве учебного пособия для студентов

Подготовлено на кафедре Экономики и Финансов

Рецензенты д-р техн. наук, проф. С.В. Егоров, д-р эконом. наук, проф. И.В. Зайцевский

Грошев Л.Н.

Количественные методы в финансовом анализе. Учебное пособие, - М.: Издательство МЭИ, 2005.- с.

ISBN 5-7046-0644-Х

В данном пособии рассматривается финансовый анализ в условиях определенности. Состоит из восьми тем, каждая из которых содержит теоретическое введение, решение типовых задач, задачи для самостоятельного решения и контрольное задание. Пособие построено таким образом, чтобы подготовить студента к самостоятельному решению задач по всем основным разделам курса (наращенные и дисконтированные суммы, потоки платежей, ренты, кредитные расчеты, оценка инвестиционных проектов).

Для студентов, обучающихся по направлениям «Экономика» и «Менеджмент».

Учебное издание

Грошев Лев Николаевич

КОЛИЧЕСТВЕННЫЕ МЕТОДЫ В ФИНАНСОВОМ АНАЛИЗЕ

Учебное пособие по курсу «Финансовая математика»

Для студентов, обучающихся по направлениям «Экономика» и «Менеджмент»

Редактор издательства Е.Н. Касьянова

ЛР № 020528 от 05.06.97г.

Темплан издания МЭИ 2000 (II), учебн. Печать офсетная

Подписано в печать 22.12.2000 г. Формат 60´84/16

Физ.печ. л. 2,5 Тираж 200 Изд № 130 Заказ Цена руб.

Издательство МЭИ, 111250, Москва, Красноказарменная, д.14

Отпечатано в типографии ЦНИИ “Электроника”, 117415, Москва,

просп. Вернадского, д.39

ISBN 5-7046-0644-Х Ó Московский Энергетический институт, 2005

ПРЕДИСЛОВИЕ

Количественные методы в финансовом анализе (финансовая математика) является одним из основных разделов финансового анализа.

Люди, посвятившие себя бизнесу, должны уметь оценивать все возможные варианты финансовых последствий, которые могут иметь место при совершении ими какой - либо сделки. Любая финансовая, кредитная или коммерческая операция сопровождается выработкой определенных соглашений между участниками сделки (например, определением суммы кредита (займа, инвестиций), установлением цены товара, выбором способов начисления процентов, установлением сроков и способов погашения долга и т.д.).

В финансовой практике нередко приходиться пересматривать заключенные ранее контракты в связи с изменившимися обстоятельствами или менять схему погашения кредита.

Ясно, что успешный итог сделки зависит от множества факторов, которые необходимо учесть уже на этапе планирования сделки. Чем тщательнее проведена предварительная работа по оценке этих факторов, тем больше вероятность того, что данная сделка даст ожидаемые результаты. Для учета множества факторов необходимо применять количественный анализ, который часто выходит за рамки элементарных арифметических расчетов.

Совокупность методов расчетов, позволяющие прояснить вышеназванные ситуации, составляют предмет данного пособия.

Финансовая математика сформировалась на стыке финансовой науки и математики и поэтому при ее изучении предполагается знание как основ рыночной экономики, так и математического анализа.

Настоящее учебное пособие, предназначенное для студентов, обучающихся по специальностям «Экономика» и «Менеджмент», позволяет за короткий срок ознакомиться с основными понятиями и применением финансовой математики. Следует отметить, что в данном пособии рассматривается финансовый анализ в условиях определенности.

Основой данного пособия послужило учебное пособие автора «Финансовая математика»

В методическом плане пособие построено таким образом, чтобы подготовить студента к самостоятельному решению задач по всем основным разделам курса (наращенные и дисконтированные суммы, потоки платежей, ренты, кредитные расчеты, оценка инвестиционных проектов).

С этой целью каждый раздел пособия содержит необходимый минимум теоретического материала, а в некоторых местах и подробное его изложение, новые понятия выделены жирным шрифтом. Приведены подробные решения типовых задач. Правильность решения некоторых задач, предназначенных для самостоятельной работы, студент может проверить по прилагаемым к ним ответам.

В конце пособия дается контрольное задание, выполнение которого необходимо для сдачи зачета (экзамена) по финансовой математике.

Контрольное задание выполняется в отдельной тетради. Решение каждой задачи должно быть подробным и обоснованным, т.е. содержать все формулы, вывод уравнений и логические рассуждения, необходимые для решения задачи. К большинству задач следует сделать рисунки по типу рис. 6 или рис. 7 данного пособия. На рисунке указывается ось времени (сроков) Ot, вдоль которой рядом с каждым сроком проставляется соответствующий ему тип платежей.

ТЕМЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО КУРСУ «ФИНАНСОВАЯ МАТЕМАТИКА»

1.Основное уравнение процентной ставки. Простые проценты. Формула простых процентов.

2.Учетная ставка. Математическое и банковское дисконтирование.

3.Реинвестирование.

4.Сложная процентная ставка. Формула сложных процентов. Вычисление наращенной суммы смешанным методом.

5.Дисконтирование по простым и сложным процентам.

6.Наращенная сумма при начислении процентов m(m> 1) раз в году.

7.Номинальная и эффективная процентные ставки.

8. Сравнение простых и сложных процентов.

9.Учет инфляции. Индекс цен. Темп инфляции. Индекс покупательной способности денег.

10. Брутто – ставка (инфляционная ставка). Определение и вывод.

11. Принцип финансовой эквивалентности. Понятие потока платежей. Эквивалентные потоки платежей, эквивалентное значение для потока платежей.

12. Эквивалентность процентных ставок.

13. Консолидация платежей.

14. Изменение условий коммерческих сделок на основе принципа финансовой эквивалентности.

15. Финансовые ренты. Классификация и параметры рент.

16. Годовая обычная рента. Современное и наращенное значение и их расчет.

17. Годовая рента при начислении процентов m раз в году.

18. P - срочная рента. Современное и наращенное значение.

19. (p,m) – рента. Современное и наращенное значение.

20. Приведенная, отложенная ренты и их современное и наращенное значение.

21. Погашение долга единовременным платежом.

22. Погашение долга равными срочными уплатами. Планирование фонда погашения долга.

23. Модель детерминированного потока платежей в инвестиционном процессе.

24. Современная стоимость (PV) потока платежей.

25. Чистая современная стоимость (NPV) потока платежей.

26. Модель непрерывного потока платежей.

27. Показатели эффективности инвестиционного проекта: ставка сравнения, чистая текущая стоимость (чистый приведенный доход), срок окупаемости инвестиционного проекта, внутренняя норма доходности, индекс рентабельности (рентабельность).

28. Расчет срока окупаемости, учитывающего фактор времени (на конкретном примере).

29. Выбор инвестиционного проекта с помощью его показателей эффективности.

30. Финансовые операции с продажей контрактов.

31. Выбор оптимального контракта для покупателя.

32. Доходность контракта для кредитора.

33. Портфель векселей (эффект продажи).

ПРОСТЫЕ ПРОЦЕНТЫ

Получая кредит в размере P рублей, заемщик обязан вернуть полученную денежную ссуду через точно оговоренный срок и уплатить ее в соответствии с установленным в договоре процентом, т. е.возвращаемая сумма Sравна:

S = P + I

Сумма Sназывается наращенной, I - процент, т. е. плата за кредит.

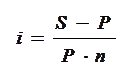Процентная ставка i определяется как относительное приращение суммы долга за единицу времени, т. е.

(1)

где n - срок ссуды. Процентная ставка i указывается до сотых долей процента. Отметим, что процентная ставка применяется не только как инструмент наращивания суммы долга, но и как измеритель степени доходности (эффективности) финансовой или кредитной операции.

Из формулы (1) получим, что наращенная сумма

S = P (1 + i×n) (2)

Это формула называется формулой простых процентов.

Пример. Кредит в сумме P = 100 тыс. руб. выдан на срок n = 2 года с условием возврата S=150 тыс. руб. Определите доходность данной финансовой операции т.е. процентную ставку.

Решение.

i = 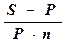= = 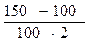0,25 или i = 25 %,

т. е. доходность финансовой операции равна 25 %.

Пример.Фирма приобрела в банке вексель, по которому через год должна получить 5му через год должна получить 6о учебное пособие автора "0 тыс. руб. В момент приобретения цена векселя составляла 40 тыс. руб. Определите доходность этой сделки.

Решение. И в этом случае доходность - это процентная ставка i.

i =(S-P) / P = 10/40 = 0,25 = 25%.

Если на последовательных интервалах времени n₁и n₂ используются простые ставки процентов i₁и i₂ , то сумма процентов, начисленных за эти два интервала, будет равна

I = I₁ + I₂ = n₁ i₁ P+ n₂ i₂× P = P(n₁ i₁ + n₂ i₂ ) (3)

Наращенная сумма за время n₁ + n₂ составит:

S = P + I = (1 + n₁ i₁ + n₂ i₂ ) (4)

Когда число временных интервалов не два, а больше, в общем случае N , тосумма процентов, начисленных за N интервалов будет равна:

I = I₁ + I₂ + .. + I_N = n₁× i₁× P+ n₂× i₂× P + ... + n_N× i_N× P

или

I = P (n₁ i₁ + n₂ i₂ +...+ n _N i _N ). (5)

Количество же слагаемых типа n_k i_kв формуле для вычисления наращенной суммы также увеличится - их будет ровно столько, сколько интервалов, т.е.

S = P + I = ( 1 + n₁ i₁ + n₂ i₂ + ...+ n_N i_N ). (6)

Пример. Процентная ставка банка по вкладам, составлявшая в начале года 12 % годовых, через полгода была уменьшена до 10% , а еще через три месяца - до 8% годовых. Определите сумму процентов за год на вклад в 100 тыс. руб.

Решение. По формуле (5), для N = 3, имеем:

I = 100 000 (0,5 × 0,12 + 0,25× 0,1 + 0,25× 004) = 9500 (руб.).

Если срок финансовой сделки выражается в днях, то n = t / K , где t - срок в днях, K =360 и формула (2) принимает вид:

S = P (1+ i × t / K)

Задачи

1.1.Годовая ставка простых процентов равна 10,5 %. Через сколько лет начальная сумма удвоится? Решите задачу в общем виде, т.е. процентную ставку принять равной i.

1.2.Фирма получила в банке ссуду в размере 2 млн руб. под 50 % годовых на срок с 15 февраля до 15 апреля (год не високосный). Определите возвращаемую сумму. Ответ: 2,164 млн руб.

1.3.Выдан в кредит 5 млн руб на 6 месяцев под простые проценты по ставке 10 % в месяц. Найдите наращенное значение долга в конце каждого месяца. Покажите, что получившиеся суммы образуют арифметическую прогрессию.

1.4.Договор предусматривает следующие ставки простых процентов: а) за первый квартал - 20 % годовых, за второй квартал - 25 % годовых, за третий квартал - 22 % годовых;

б) за первый квартал - 10 % ежемесячно, за второй и третий кварталы-20 % ежемесячно, за четвертый квартал - 30 % ежемесячно.

Определите коэффициент наращения за год в каждом из двух вариантов.

1.5.На некоторую сумму ежемесячно в течение квартала начисляются простые проценты по ставке 9 % в первый месяц, 10 % - во второй, 11 % - в третий. Определите коэффициент наращения за квартал при реинвестировании. (Операция, при которой в момент каждого изменения ставки, наращенная к этому моменту сумма вкладывается вновь под простой процент, называется реинвестированием). Ответ: 1,319

1.6.Определите коэффициент наращения в предыдущей задаче без реинвестирования. Ответ: 1,30.

ДИСКОНТИРОВАНИЕ

При дисконтировании решается задача, обратная вычислению наращенной суммы, т.е. по заданной заранее наращенной сумме S определить, какую сумму P надо инвестировать, чтобы через время t при постоянной ставке простого процента i получить сумму S. Из формулы (2) следует, что

сумма P называется современным или приведенным значением

будущей суммы S. Операция вычисления современной стоимости будущей суммы денег называется математическим дисконтированием, а величина -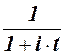

дисконтирующим множителем.

Разность D = S - Pназывают дисконтомсуммы.

Пример. Заемщик получил кредит на 6 месяцев под 20 % годовых с условием вернуть 300 тыс. руб. Какую сумму получил заемщик в момент заключения договора?

Решение. Принимая год равным 360 дням, а 6 месяцев - 180 дням, получим

S = 300 /( 1 + 0,20 × 180/360 ) = 272,73 тыс. руб.;

Пример. Какую сумму инвестор должен внести сегодня под простые проценты по ставке 50 % годовых, чтобы накопить 100 тыс. руб.: а) за полгода; б) за два года.

Решение. Имеем ( в рублях) :

а) S = 100 000 /(1 + 0,5 × 0,5) = 80 000;

б) S = 100 000 /(1 + 0,5 × 2) = 50 000.

Второй вид дисконтирования называется банковским учетом. Суть его в следующем. Банк приобретает вексель у вкладчика до наступления срока платежа по цене, которая меньше суммы, указанной на векселе, т.е. учитывает вексель сдисконтом (скидкой).

При учете векселя применяется банковский учет. Для этого банк вводит учетную ставку d . Размер дисконта D = S× n × d, где d - годовая учетная ставка, n-срок от момента учета до даты погашения векселя в годах. Сумма, которую получит вкладчик при учете векселя, равна

P = S – S × n × d = S ( 1 - n × d).

Учет производится по банковскому правилу, т. е. К = 360 (число дней ссуды точное). Соотношение между учетной ставкой банка d и процентной ставкой i за один период следующее:

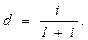( 7)

Пример. Тратта (переводной вексель) выдан на сумму 100 тыс. руб. с уплатой 18 ноября. Владелец векселя учел его в банке 24 сентября по учетной ставке 20%. Определите сумму, полученную при учете.

Решение. Срок от момента учета до даты погашения равен 55 дням. Тогда искомая сумма равна:

P = S (1 - n × d ) = 100 000 ( 1 - 55/360 × 0,2 ) = 96 944,4 руб.

Дисконт составит 100 000 - 96 944,4 = 3 055,6 руб.

Задачи

2.1. Вексель, выданный на сумму 15 000 руб. с уплатой через 100 дней, с условием начисления простых процентов по ставке 10 % годовых, был учтен в банке за 50 дней до наступления срока по простой учетной ставке 15%. Определите полученную владельцем сумму при учете векселя и величину дисконта, полученную банком.

2.2. Владелец векселя в 100 тыс. руб. со сроком погашения 5 мес. учитывает его в банке спустя два месяца. Банк учитывает вексель за 94 тыс. руб. Определите дисконт D, d₃ - учетную ставку банка за 3 месяца, годовую учетную ставку d и учетную стоимость векселя за месяц до погашения. Ответ: D = 2 тыс. руб.; d₃ = 0,06; d = 0,24 ; P = 98 тыс. руб.

2.3. Вексель выписан 10 января 1998 года с датой погашения 10 октября 1998 года. Проценты по векселю начисляются по ставке 12 % в год. Определите учетную (выкупную) стоимость векселя, если вексель учтен в банке 10 мая 1998 года по учетной ставке 10 %. Ответ: 104,422 тыс. руб.

2.4.Выведите соотношение (7).

СЛОЖНЫЕ ПРОЦЕНТЫ

В отличие от простых процентов, база для начисления сложных процентов будет увеличиваться с каждым периодом начисления.

Если положить в банк сумму P и банк выплачивает сложные проценты по годовой ставкеi, то через год сумма будет равна

S₁ = P + I = P + iP = P (1+ i),

где I = iP– процент, начисленный за первый год. В конце второго года вкладчик получит сумму:

S₂ = P+Pi+(P+Pi) i = P (1+ i)².

Присоединение начисленных процентов к их базовой сумме называется капитализацией процентов.

Несложно понять, что через n лет вкладчик получит сумму

S_n = P ( 1+ i )ⁿ. ( 8)

Формула (8) называется формулой сложных процентов. В общем случае в формуле (8) n - число периодов начисления (n может быть и нецелым), i - ставка за период. Величина (1 + i)ⁿ называется коэффициентом наращения.

Пример. Депозит в размере 500 тыс. руб. положен в банк на 3 года. Определите сумму начисленных процентов по простой и сложной ставках, если годовая ставка составляет 80 %.

Решение.По простой ставке I = P ·n ·i = 500 ·3 · 0,8 = 1200 тыс. руб.

По сложной ставке I = P[( 1+ i )ⁿ - 1] =500 [(1+ 0,8)³ - 1] = 2416 тыс. руб.

Пример.Сберегательный банк начисляет ежегодно 8 % сложных. Клиент положил в банк 20 000 руб. Какая сумма будет на счету клиента через 6 лет и три месяца?

Решение. По формуле (8), где n = 6,25,P = 20 000, находим:

S = 20 000(1+0,08)^6,25 = 32 354,04 руб.

При дробном числе лет можно применять смешанный метод, который предполагает начисление процентов за целое число лет по формуле сложных процентов и по формуле простых процентов за дробную часть периода, т. е.

S_n = P ( 1+ i )^a ( 1 + i· b),( 9 )

где a- целое число периодов (лет), b - дробная часть периода (года).

В качестве иллюстрации этой формулы используем предыдущий пример. Имеем:

S = 20 000 (1+ 0,08)⁶ (1 + 0,25 ·0,08) = 32 372,24 руб.