Начисление процентов в условиях инфляции и налогообложения

Инфляция характеризуется обесцениванием национальной валюты, снижением ее покупательной способности и общим повышением цен в стране. Поэтому определены количественные соотношения по определению влияния инфляции на показатели финансовой операции.

Основной признак инфляции – это рост цен в среднем всех групп товаров и услуг, усредненной цены всей номенклатуры потребительской корзины. Товары и услуги выбираются в качестве базы выявления уровня инфляции. В зависимости от состава выбранных товаров количественное выражение уровня инфляции будет разным.

Все показатели финансовой операции можно разделить на две группы: номинальные, рассчитанные в текущих ценах, и реальные, учитывающие влияние инфляции, рассчитанные в сопоставимых ценах базисного периода.

Рассмотрим различные варианты начисления процентов в условиях инфляции:

1. Индекс цен. Пусть выбран определенный набор товаров и услуг и пусть за время t его стоимость изменилась от суммы Р₁ к сумме Р₂. Индексом цен за время t называется величина
I_p^(t)=P₂/P₁. Индекс цен (индекс инфляции) показывает, во сколько раз выросли цены за рассматриваемый период. Наиболее часто используется индекс потребительских цен.

2. Темп инфляции за время t:

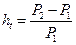. Темп инфляции *на100 показывает, на сколько процентов выросли цены за время t. Формально определение темпа инфляции совпадает с определением процентной ставки, а определение индекса цен напоминает определение индекса роста суммы.

3. Соотношение между индексом инфляции и темпом инфляции за время t: I_p^(t)=1+h_t.

4. Если известны индексы цен или темпы инфляции за последовательные периоды времени, то индекс цен за все периоды времени
t= t₁ + t₂ + …+ t_k будет равен произведению индексов цен за последовательные промежутки времени: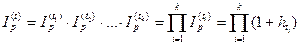

Пример 1. Определить годовой индекс инфляции, если известен среднемесячный темп инфляции 3%

Решение. Будем измерять время в годах и воспользуемся формулой из 4 пункта. Тогда

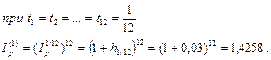
Ответ: при темпе инфляции 3% в месяц цены за год увеличатся более чем в 1,42 раза.

5. Пусть на капитал Р происходит наращение простых процентов по ставке r в течение времени n и индекс цен равен 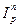, тогда наращение суммы с учетом обесценения капитала будет:

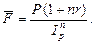
6. В этом случае реальное наращение первоначального капитала с учетом покупательной способности денег будет только в том случае, если 1+nr>I_p⁽ⁿ⁾.

7. Начисления для простых процентов 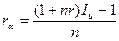, где
r_a - простая ставка процентов, учитывающая инфляцию, дает такое же наращение капитала на одну денежную единицу, что и r;
I_и – индекс инфляции, который показывает, во сколько раз выросли цены за некоторый промежуток времени.

8. Для сложных процентов начисление производится по следующей формуле: 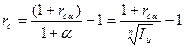, где r_ca - сложная ставка процентов, учитывающая инфляцию; a - темп инфляции (относительная величина уровня инфляции), который связан с индексом инфляции равенством I_p⁽ⁿ⁾=1+a.

9. Для начисления номинальной процентной ставки, учитывающей инфляцию, используется уравнение: 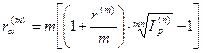, где r_a^(m) -номинальная ставка с учетом инфляции.
Пример. На вклад в 30 тыс. руб. ежемесячно начисляются сложные проценты по номинальной годовой процентной ставке 40%. Оценить сумму вклада через 1,5 года с точки зрения покупательной способности, если ожидаемый темп инфляции 2% в месяц. Какова должна быть величина положительной процентной ставки? Как изменится ситуация, если темп инфляции будет 4% в месяц?
Решение.

a. за полтора года сумма вклада составит
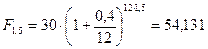тыс. руб.

b. индекс инфляции за 1,5 года при темпе инфляции 2% в месяц составит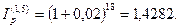

c. найдем величину вклада с точки зрения ее покупательной способности 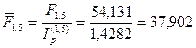тыс. руб.

d. найдем реальный доход владельца вклада: 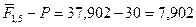тыс. руб.

e. положительная процентная ставка должна удовлетворять неравенству: 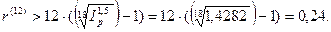Таким образом, при темпе инфляции 2% в месяц и ежемесячном начислении сложных процентов реальное наращение капитала будет происходить только при процентной ставке, превышающей 24%.

f. При темпе инфляции 4% в месяц 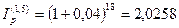, 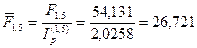и реальный доход вкладчика составит 26,721-30=-3,279 тыс. руб., т.е. в этом случае вкладчик понесет убытки. В этих условиях для положительной процентной ставки должно выполняться неравенство: 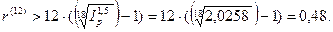Для обеспечения реальной доходности согласно коэффициенту наращения необходимо так индексировать исходную ставку (увеличить на инфляционную премию), чтобы новый коэффициент наращения полностью компенсировал потери от инфляции. Для этого его надо помножить на корень n-степени из индекса инфляции. И далее можно найти величину положительной процентной ставки по формуле 9: при темпе инфляции 2% в месяц находим ставки r⁽¹²⁾=0,648, т.е. ставка 64,8% годовых при ежемесячном начислении сложными процентами и данном темпе инфляции обеспечивает реальную доходность в 40% годовых.

10. При m=1 положительная процентная ставка равна r = r+a+ra. Это равенство называется формулой Фишера, а величина a+ra называется инфляционной премией, которую необходимо прибавить к исходной ставке доходности для компенсации инфляционных потерь.

11. Для начисления номинальной процентной ставки используется уравнение: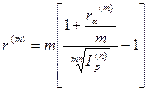

Пример. Банк предлагает клиентам помещать деньги на депозит на один год под 32% годовых с ежеквартальным начислением сложных процентов. Найти реальную доходность такого предложения для клиентов банка, если ежемесячный индекс инфляции прогнозируется равным 1,02.

Решение. 1. Найдем индекс инфляции за один год: I_p⁽¹⁾=1,02¹²=1,2682.

2. По формуле 11 при m=4, r_a⁽⁴⁾=0,32, получим r⁽⁴⁾=4 [(1+0,32/4)/1,2682^1/4-1]=0,0709. Т.о., реальная доходность при помещении денег на депозит будет составлять примерно 7,09% годовых.

12. Для простой учетной ставки, учитывающей инфляцию .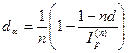

13. Для сложной учетной ставки, учитывающей инфляцию .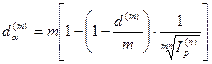

Пример. На сумму в 5 тыс. руб. в течение трех месяцев начислялись простые проценты по ставке 40% годовых. За каждый месяц цены росли соответственно на 15, 12 и 10%. Найти наращенную сумму с учетом инфляции и величину положительной процентной ставки, при которой будет происходить реальное увеличение капитала.

Решение. 1. Найдем индексы цен по месяцам: 1,15; 1,12 и 1,1.

2. Индекс цен за квартал (t=0,25 часть года) I=1,15*1,12*1,1=1,4168.

3. Наращенная сумма с учетом инфляции = (1+0,25*0,4)/1,4168=3,882 тыс. руб.

4.Минимально допустимая процентная ставка, при которой не происходит реального уменьшения капитала, получается из соотношения

1+n*r>I_p⁽ⁿ⁾. Из равенства левой и правой части найдем r=( I_p⁽ⁿ⁾-1)/n. Тогда наращение капитала только компенсирует действие инфляции. r^*=(1.4168-1)/0.25=1.6672. Следовательно, при данном росте цен реальное наращение капитала будет происходить только при ставке, превышающей 166,72%.