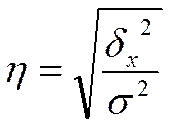Дисперсия, ее св-ва и методы расчета. Дисперсия альтернативного признака

Дисперсия –ср квадрат отклонения всех значений признака ряда распределения от ср. арифметической. Обозначается дисперсия буквой 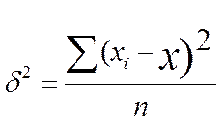, где х_i – индивид значение признака (варианта), х – ср. арифм-ая, n – численность сов-ти. Данная ф-ла явл простой. Взвешенная фор-ла дисперсии будет иметь вид: 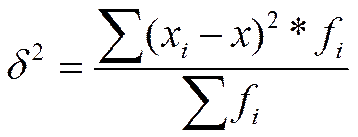, где х_i – индивид значение признака (варианта), х – ср. арифм-ая, f – число единиц сов-сти с одним и тем же значением признака.

СВ-ВА ДИСПЕРСИИ. 1. б² 1. б²(а) = 0 – дисперсия постоянной величины равна нулю. 2. б²(а+х) = б²(х) – дисперсия не меняется, если все варианты увеличить/уменишить на одно и то же число. 3. б²(ах) = а² * б²(х) – постоянный множитель выносится за знак дисперсии возведенным в квадрат. Или: если все варианты умножить на число а, дисперсия увеличится в а² раз. 4. 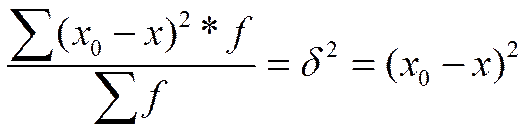- это св-во носит название св-ва min-ти дисперсии от средней. Дисперсия от средней меньше, чем средний квадрат отклонения от любого числа х₀ на (х₀ – х)².

Исп-ние св-в дисперсии позвол упрощать ее расчеты, особенно в тех случаях, когда вариац ряд сост арифм прогрессию или имеет равные интервалы. В этих случаях сначала находят дисперсию от условн нуля, а затем использ 4-е св-во дисперсии, переходят к дисперсии от средней.

Правило сложения дисперсий и его использование в анализе взаимосвязей.

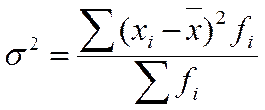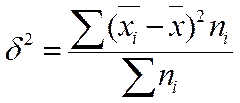Если данн представ в виде аналит группировки, то можно вычисл дисперсию общ, межгрупповую и внутригрупповую. Общ дисперсия измеряет вариацию признака во всей сов-ти под влиянием всех факторов, обуславлив эту вариацию. (1) (2)

Межгруп дисперсияхар-ет систематич вариацию, т.е. различия в величине изуч признака, воз­ник под влиянием признака-фактора, положен в основание группировки. Она рассчит по формуле 2:

Внутригруп дисперсия отражает случайную вариа­цию, т.е. часть вариации, происходящую под влиянием неуч­тенных факторов и не зависящ от признака-фактора, поло­женного в основание группировки. Она исчисляется след обр:

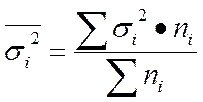(3) (4)

Средняя из внутригрупповых дисперсий (4):

ПРАВИЛО СЛОЖЕНИЯ ДИСПЕРСИЙ: Об­щая дисперсия равна сумме средней из внутригруп и межгрупповых дисперсий: σ² =δ_х²+σ¯_i² Суть: общая дисперсия возник под влиянием всех факторов, равна сумме дисперсий, воз­ник под влиянием прочих фак-в, и дисперсии, возник за счет группировочного пр-ка.

Зная любые два вида дисперсий, можно опр или проверить правильность расчета третьего вида.

На основании правила сложения дисперсий можно опр показатель тесноты связи между группировоч (факторным) и результат при-ми. Он наз-ся эмпирическим корреляционным отношениеми рассчитыва­ется по формуле: