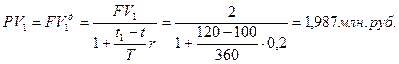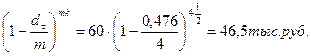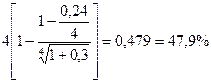Сложная учетная ставка и инфляция

Номинальная стоимость векселя, дисконтированного m раз в году, через k лет определяется по формуле (4.12)

FV = .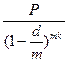

Пусть годовой уровень инфляции t. Рассуждая как в предыдущем разделе, запишем

FV_t = FV (1 + t)^k.

Эта формула имеет смысл лишь для k £ 1, т.к. от года к году уровень инфляции меняется.

Введем d_t - номинальную учетную ставку, исправленную на инфляцию.

FV_t = 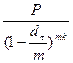. (4.18)

Сопоставляя (4.12) и (4.18), получим

d_t = 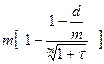(4.19)

PV=FVt dt = Пример 4.7 Владелец векселя на сумму 60 тыс. руб. со сроком погашения 1/2 года учел его в банке по номинальной учетной ставке 24%. Дисконтирование квартальное. Годовой уровень инфляции 30%. Определите текущую стоимость векселя и номинальную учетную ставку банка с учетом инфляции.

Решение

FV_t = 60 тыс. руб.

k=1/2

t = 0,3

m = 4

d = 0,24

PV = ? , d_t = ?

ОБЪЕДИНЕНИЕ ВЕКСЕЛЕЙ

Объединение ряда платежных обязательств в финансовой практике называется консолидацией.

Итак, имеются векселя с номинальной стоимостью FV₁, FV₂,…FV_n и сроком погашения k₁, k₂,…k_n соответственно. Нужно рассчитать стоимость FV или срок k объединенного векселя.

Определение стоимости объединенного векселя

Постановка задачи: задан срок погашения объединенного векселя. Требуется рассчитать его стоимость.

Идея метода расчета. 1) Номинальные стоимости всех векселей приводятся к стоимости на момент погашения объединенного векселя по формулам простых и сложных процентов. 2) Стоимость объединенного векселя равна сумме приведенных стоимостей всех векселей.

Объединение векселей на основе простых процентов

Приведем стоимости всех векселей к моменту погашения консолидированного векселя. К этому моменту стоимости FV2 и FV3 нарастут, т. к. t >.t2 и t > t3. Пример 4.8Четыре векселя номинальной стоимостью 2 млн. , 6, 8 и 10 млн. руб. со сроками погашения 120, 80, 90 и 130 дней нужно объединить в один со сроком погашения 100 дней. Консолидация происходит по простой процентной ставке 12% и банковской методике. Определите стоимость объединенного векселя.

Решение

FV₁ = 2 млн. р.; t₁ = 120 дн.

FV₂ = 6 млн. р.; t₂ = 80 дн.

FV₃ = 8 млн. р.; t₃ = 90 дн.

FV₄ = 10 млн. р.; t₄ = 130 дн.

r = 0,12

t = 100

FV = ? По ставке простых процентов наращенная стоимость этих векселей

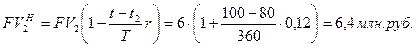
Здесь t –t₂ - срок, оставшийся до погашения объединенного векселя. Аналогично

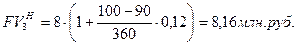
Для первого и четвертого векселей t₁ > t и t₄ > t .

Следовательно, они будут реализовываться по заниженной, дисконтированной стоимости.