Типовые примеры и методы их решения. Пример 1.9.1. Согласно новому финансовому соглашению платеж 80 тыс

Пример 1.9.1. Согласно новому финансовому соглашению платеж 80 тыс. руб. со сроком уплаты 6 месяцев заменяется платежом со сроком уплаты: а) 3 месяца; б) 9 месяцев. Найдите величину нового платежа, если используется простая процентная ставка 40% годовых.

Решение. Пусть Р₁ = 80 тыс. руб., г = 0,4. Считая, что год содержит 360 дней и каждый месяц - 30 дней, полагаем n = 0,5 года.

а) Полагая n₀ = 0,25 года и учитывая, что n₀ < n₁, по формуле (49)получим:

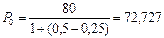тыс. руб.

Этот же результат можно получить, и не пользуясь формулой (49), а составив для данной конкретной ситуации уравнение эквивалентности, руководствуясь принципом финансовой эквивалентности. В соответствии с этим принципом величина платежа Р₀ должна быть такой, что, получив через 3 месяца (n₀ = 0,25 года) Р₀ и инвестировав эту сумму под простую процентную ставку r = 0,4, кредитор через время n₁-n₀ - по мог бы получить сумму P_l = 80 тыс. руб. Таким образом, получим уравнение:

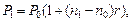
в котором неизвестной величиной будет Р₀.

Обратим внимание на следующий факт. Если не применять принцип финансовой эквивалентности, а просто воспользоваться равенством приведенных стоимостей (на начальный момент времени) этих платежей, т.е. соотношением

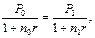
то платеж Р₀ будет равен:

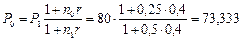тыс. руб.

Эта сумма больше, чем 72,727 тыс. руб. Инвестировав 73,333 тыс. руб. под 40% годовых, кредитор через 3 месяца (n₁ – n₀ =0,2 года) получил бы 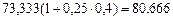тыс. руб., т.е. на 666 руб. больше, чем было предусмотрено первым финансовым соглашением.

б) Поскольку в этом случае n₀ = 0,75 и п₀ >n₁, то по формуле (49)получим:

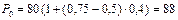тыс. руб.

Согласно принципу финансовой эквивалентности в этом случае величина платежа Р₀ должна быть такой, что, получив через 6 месяцев (n₁ = 0,5 года) сумму Р₁ = 80 тыс. руб. и инвестировав эту сумму под простую процентную ставку r=0,4, кредитор через время n₀ – n₁мог бы получить сумму Р₀. Следовательно, Р₀ находится из уравнения Р₀ =P₁(l+(n₀ – n₁)r), совпадающего по виду с примененной формулой.

Если же просто воспользоваться равенством приведенных стоимостей, то

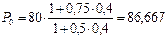тыс. руб.

что меньше, чем 88 тыс. руб. Т.е. кредитору не имеет смысла менять условия соглашения, так как по первому контракту он может получить больше.

Пример 1.9.2. Найдите величину нового срока, если платеж в 20 тыс. руб. с уплатой через 250 дней предполагается заменить платежом в 18 тыс. руб. Используется простая процентная ставка 35% годовых, и расчетное число дней в году равно 360.

Решение. Очевидно, что так как 18 тыс. руб. меньше 20 тыс. руб., то новый срок n₀ должен быть меньше 250 дней. Полагая P₁=20 тыс. руб., n₁-250/360 года, P₀=18 тыс. руб., r=0,35, по формуле (50) для случая P₀ <P_l получим:

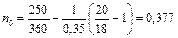года, или n₀ 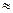135 дней.,

Проверим этот результат. Пусть через 135 дней кредитор получит 18 тыс. руб., тогда, инвестировав эту сумму на 115 дней (0,319 года) под простую процентную ставку 35% годовых, он получит 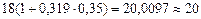тыс. руб. Таким образом, с изменением финансового соглашения кредитор убытка не понесет, поскольку через общий срок, равный 250 дням (135 + +115), он получит 20 тыс. руб., как и в первоначальном варианте контракта.

Обратим внимание, что платеж в 20 тыс. руб. нельзя заменить любым платежом Р₀, меньшим этой суммы. По смыслу Р₀ не может быть меньше приведенной к начальному моменту величины капитала Р₁ , т.е. 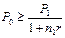(что и указано в формуле (50)). В условиях разобранного примера:

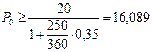тыс. руб.

Пример 1.9.3. Платежи в 6, 4 и 10 тыс. руб. должны быть погашены соответственно через 90, 165 и 270 дней. Кредитор и должник согласились заменить три платежа одним через 120 дней. Найдите величину консолидированного платежа, если используется простая процентная ставка 38% годовых и в расчет принимаются обыкновенные проценты.

Решение. При решении задач такого типа пользуются уравнением эквивалентности, согласно которому сумма заменяемых платежей, приведенных к одному моменту времени, приравнивается к сумме платежей по новому соглашению, приведенных к той же дате. Причем приведение осуществляется путем дисконтирования к более ранней дате или путем наращения величины соответствующего платежа, если эта дата относится к будущему.

В данном случае платежи в 6, 4 и 10 тыс. руб. заменяются единым платежом Р₀, величину которого обычно определяют путем приведения всех платежей к дате погашения платежа Р₀.

Так как срок погашения платежа в 6 тыс. руб. меньше 120 дней, то процесс приведения для этого платежа будет осуществляться в виде процесса наращения в течение 30 дней (120 - 90) по простой процентной ставке 38% годовых.

Так как срок погашения платежа в 4 тыс. руб. больше 120 дней, то процесс приведения для этого платежа будет осуществляться в виде процесса дисконтирования по простой процентной ставке 38% годовых за 45 дней (165 - 120). По той же причине сумма 10 тыс. руб. дисконтируется за 150 дней (270 - 120).

Складывая приведенные суммы платежей, получим величину консолидированного платежа Р₀:

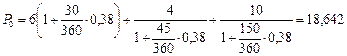тыс. руб.

Если бы за дату приведения выбрали, например, время выплаты платежа в 6 тыс. руб., то, рассуждая, как и выше, получили бы такое уравнение:

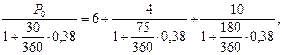
откуда P₀=18,683 тыс. руб.

При выборе в качестве даты приведения момент отсчета всех сроков получим уравнение:

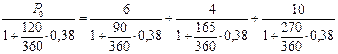
из которого находим, что P₀ = 18,780 тыс. руб.

Отличие результатов из-за выбора даты приведения обусловлено правилами наращения и дисконтирования по простым процентам. Поэтому при изменении финансового соглашения необходимо оговорить дату, на которую будет осуществляться

приведение всех сумм.

Если же рассматривать в общем виде задачу замены платежей P₁ , P₂ ,…, P_m выплачиваемых соответственно через время n₁, n₂,...,n_m, одним платежом Р₀ с выплатой через время n₀, то, рассуждая, как и выше, можно получить путем приведения всех платежей к дате выплаты платежа Р₀ уравнение эквивалентности, в правой части которого платежу Р_i будет соответствовать слагаемое 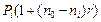, если n₀ 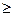n_i, платежу Р_j будет соответствовать слагаемое 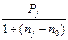, если n₀< n_j,.Таким образом, уравнение имеет вид:

,

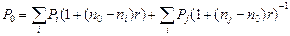где в первой сумме происходит суммирование по тем i, для которых выполнено n₀ 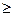n_i и,, а во второй сумме - по тем j, для которых n₀ < n_i,.

Пример 1.9.4. Платежи в 3 тыс. руб., 5 тыс. руб. и 7 тыс. руб. должны быть внесены через соответственно 70, 130 и 180 дней. Было достигнуто соглашение заменить три платежа одним, равным им сумме. Определите срок уплаты консолидированного платежа, если используется простая процентная ставка 32% годовых в условиях начисления обыкновенных процентов.

Решение. На практике для определения срока по консолидированного платежа дисконтируют все величины платежей на начальный момент и затем приравнивают приведенную стоимость консолидированного платежа к сумме приведенных стоимостей исходных платежей. Решая полученное уравнение относительно n₀, находим искомый срок.

Итак, находим вначале дисконтированные стоимости исходных платежей:.

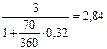тыс. руб., 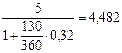тыс. руб.,

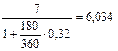тыс. руб.

Поскольку приведенная стоимость консолидированного платежа равна 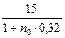тыс. руб., то приходим к уравнению:

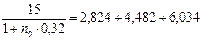, решая которое, находим по = 0,389 года, или по = 140 дням.

Можно было и сразу воспользоваться формулой (51), полагая P_l=3 тыс. руб., P₂=5 тыс. руб., P₃=7 тыс. руб., P₀=15тыс. руб., n₁= 70/360 года, n₂ =130/360 года, n₃ =180/360 года, r=0,32:

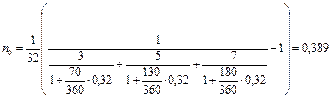
Обратим внимание, что пользоваться формулой (51) можно только в том случае, когда справедливо неравенство 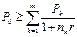. В противном случае эта формула даст отрицательныезначения срока n_o.

Если 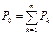, n₀r<1, и n_kr<1 для всех k, то вместо формулы (51) можно воспользоваться ее приближенным вариантом - формулой определения среднего срока (31). В изложенном примере указанные условия выполнены, поэтому (считая сразу днях): 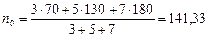дня, т.е. полученный результат отличается от ранее определенного на один день.

Пример 1.9.5. Согласно контракту предприниматель должен выплатить кредитору 10 тыс. руб. через год, 40 тыс. руб. - через 3 года и 30 тыс. руб. - через 5 лет< Предприниматель предлагает выплатить 30 тыс. руб. через 2 года и 40 тыс. руб. - через 4 года. Являются ли эти контракты эквивалентными, если в расчетах используется простая процентная ставка 34% годовых?

Решение. Два контракта считаются эквивалентными, если приведенные стоимости потоков платежей по этим контрактам одинаковы. В качестве даты приведения обычно принимают дату, от которой измеряются все сроки. В данном случае - это момент заключения контракта.

Сумма приведенных стоимостей платежей по первому контракту составит:

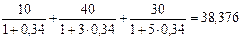тыс. руб

Аналогичным образом для второго контракта получим:

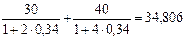тыс. руб.

Таким образом, первый контракт для кредитора выгоднее.

Пример 1.9.6. Имеется обязательство выплатить суммы 16 тыс. руб. и 24 тыс. руб. соответственно 12 апреля и 1 сентября. Стороны решили пересмотреть порядок выплат: 10 тыс. руб. выплачиваются 20 мая, 8 тыс. руб. - 10 июля и остаток долга погашается 1 августа. Определить величину третьего платежа, если пересчет осуществляется по простой процентной ставке, равной 40% годовых, по способу 365/365. Все операции производятся в пределах одного невисокосного года.

Решение. За дату приведения примем 12 апреля - время выплаты 16 тыс. руб. Для лучшего понимания вида уравнения эквивалентности в данном случае укажем явным образом порядковые номера в году представленных в контракте дат: 12 апреля - 102; 1 сентября - 244; 20 мая - 140; 10 июля - 191; 1 августа - 213. Обозначая остаток долга через Р, запишем уравнение эквивалентности:

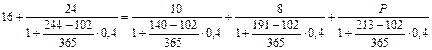
решая которое относительно Р, найдем Р = 22,297 тыс. руб.

Пример 1.9.7. Требуется заменить вексель на сумму 18 тыс. руб. со сроком погашения через 60 дней векселем со сроком погашения через 25 дней. В расчетах применяется простая учетная ставка 30% годовых и считается, что в году 360 дней.

Решение. Полагая P₁=18 тыс. руб., n₁= 60/360 года, n₀ =25/360 года, J=0,3 и учитывая, что n₀ <n₁, по формуле (52) получим:

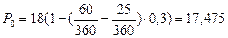тыс. руб.

Пример 1.9.8. Определите величину нового срока при замене платежа 40 тыс. руб. со сроком уплаты 75 дней платежом 46 тыс. руб., если расчеты осуществляются с помощью простой учетной ставки 32% годовых на базе финансового года, равного 360 дням.

Решение. Пусть P₁=40 тыс. руб., n₁= 75/360 года, P₀ = 46 тыс. руб., d = 0,32. Учитывая, что P₀>P₁, по формуле (53) получим:

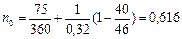
Пример 1.9.9. Владелец векселей на сумму 3,5 тыс. руб., 9 тыс. руб. и 6 тыс. руб. со сроками погашения соответственно 14 июня, 20 августа и 5 октября согласился с предложением должника об объединении трех векселей в один со сроком погашения 10 сентября того же года. Какую сумму необходимо проставить в консолидированном векселе, если используется простая учетная ставка и способ 365/360?

Решение. Используя учетную ставку 30% годовых, осуществим приведение всех сумм на 10 сентября - дату погашения консолидированного векселя.

Так как срок погашения первого векселя меньше даты приведения, то на сумму 3,5 тыс. руб. происходит наращение простыми процентами по учетной ставке в течение 88 (253 - 165) дней. По той же причине осуществляется наращение в течение 21 (253 - 232) дня на сумму 9 тыс. руб. Вексель на сумму 6 тыс. руб. учитывается за 25 (278 - 253) дней.

Складывая приведенные суммы, поучим величину Р_о консолидированного векселя:

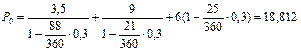тыс. руб.

Вообще, рассматривая задачу консолидации платежей P₁,P₂,…P_m, выплачиваемых соответственно через время n₁,n₂…n_m, с применением учетной ставки d и выбирая за дату приведения момент уплаты консолидированного платежа Р₀, с помощью рассуждений, как и при решении примера, можно получить следующее уравнение эквивалентности:

,

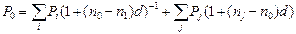где в первой сумме происходит суммирование по тем i, для которых выполнено n₀≥n_i,, а во второй сумме - по тем j, для которых n₀≤ n_j.

Пример 1.9.10. В соответствии с контрактом предприниматель должен выплатить кредитору суммы в размерах 12, 20 и 50 тыс. руб. через 90, 120 и 210 дней после 15 марта. Однако было принято совместное решение погасить все суммы единым платежом в 72 тыс. руб. Найдите дату уплаты консолидированного платежа, если используется простая учетная ставка 34% годовых на базе финансового года, равного 360 дням.

Решение, Для пояснения существа дела покажем вначале, как в данном случае можно составить уравнение эквивалентности для определения срока консолидированного платежа. Как и при использовании простой процентной ставки, в этой ситуации для определения срока консолидированного платежа осуществляют дисконтирование всех сумм по простой учетной ставке на начальный момент (в примере - 15 марта) и затем приравнивают приведенную стоимость консолидированного платежа к сумме приведенных стоимостей исходных платежей. Решая полученное уравнение относительно hq , находят искомый срок.

Итак, находим вначале дисконтированные стоимости исходных платежей:

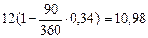тыс. руб.,

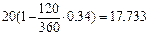тыс. руб.,

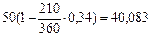тыс. руб.

Так как приведенная стоимость консолидированного платежа равна 72(1 – n₀ • 0,34) тыс. руб., то уравнение примет вид:

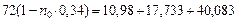, решая которое, находим ну =-0,131 года, или "о =47 дней. Отсчитывая от 15 марта 47 дней, получим 1 мая - дату уплаты консолидированного платежа.

Можно и сразу воспользоваться формулой (54), полагая P₁ = 12 тыс. руб., P₂ =20 тыс. руб., P₃ =50 тыс. руб., P₀=72 тыс. руб., n₁=90/360 года, n₂=120/360 года, n₃=210/360 года, d=0,34:

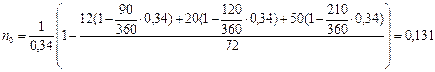
В заключение отметим, что условие этого примера можно было записать и в таком виде: требуется заменить три векселя на суммы 12, 20 и 50 тыс. руб. со сроками погашения через 90, 120 и 210 дней одним векселем на сумму 72 тыс. руб. Тогда необходимо было бы найти срок погашения нового векселя. Кстати, согласно формуле (54), новый вексель не может быть выписан на сумму, меньшую 68,796 тыс. руб.

Глава 2 СЛОЖНЫЕ ПРОЦЕНТЫ

Сложная процентная ставка

Основные положения

· Полагают, что инвестиция сделана на условиях сложного процента, если очередной доход за период исчисляется не с исходной величины инвестированного капитала (как для простых процентов), а с общей суммы, включающей также и ранее начисленные, и не востребованные инвестором проценты. В этом случае происходит капитализация процентов, т.е. присоединение начисленных процентов к их базе, и, следовательно, база, с которой начисляются проценты, все время возрастает.

· Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает.

· Формула наращения по сложным процентам является одной из базовых формул в финансовых вычислениях, поэтому для удобства пользования значения множителя наращения табулированы для различных значений процентной ставки и числа периодов начисления.

· Для кредитора более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода); более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно); обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.

· При заключении финансового соглашения на время, не равное целому числу лет, проценты, как правило, начисляются либо по схеме сложных процентов, либо по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов - для дробной части года). Наращенная сумма будет больше при использовании смешанной схемы. Аналогичные способы начисления процентов применяются и в том случае, когда базовый период начисления процентов отличен от года (например, квартал, месяц и т.п.).

· В случае нецелого числа лет кроме схемы сложных процентов и смешанной схемы возможны и другие методы начисления процентов.

· В практических расчетах для наглядной и быстрой оценки эффективности предлагаемой ставки наращения при реализации схемы сложных процентов пользуются приблизительным расчетом времени, необходимого для удвоения инвестированной суммы, известным как "правило 72-х". Это правило хорошо срабатывает для небольших значений процентной ставки.

· С увеличением частоты начисления сложных процентов по номинальной процентной ставке растет величина наращенной суммы.

· При проведении сравнительного анализа эффективности финансовых контрактов используется эффективная годовая процентная ставка - это годовая ставка сложных процентов, обеспечивающая тот же финансовый результат, что и начисление процентов несколько раз в год по номинальной ставке, деленной на число периодов начисления. Номинальная годовая процентная ставка может существенно отличаться от соответствующей ей эффективной годовой процентной ставки.

· В финансовых соглашениях не имеет значения, какую из ставок указывать - эффективную или номинальную, поскольку использование как одной, так и другой дает одну и ту же (с любой точностью приближения) наращенную сумму.

· Для анализа эффективности разнообразных финансовых контрактов эффективную процентную ставку определяют и как сложную ставку, обеспечивающую переход от начальной суммы к наращенной при однократном начислении процентов за базо­вый период (например, за год), т.е. не используя явным образом номинальную ставку.

· Математическим дисконтированием (дисконтированием по сложной процентной ставке) называется задача нахождения такой величины первоначального капитала, которая через заданное количество времени при наращении по сложной процентной ставке обеспечит получение планируемой суммы. Значения множителя дисконтирования (его также называют дисконтным множителем) табулированы для различных значений процентной ставки и числа периодов дисконтирования.

· Определяя процентную ставку в множителе дисконтирования, обычно исходят из так называемого безопасного (или гарантированного) уровня доходности финансовых инвестиций, который обеспечивается государственным банком по вкладам или при операциях с ценными бумагами. При этом может даваться надбавка за риск, причем, чем более рисковым считается рассматриваемый проект или финансовый контракт, тем больше размер премии за риск.

· При использовании сложной процентной ставки будущие поступления, являющиеся разновременными суммами, можно оценивать с позиции любого момента времени.