Начисление процентов в условиях инфляции

Следствием инфляции является падение покупательной способности денег, которое за период п характеризуется индексом J_n. Индекс покупательной способностиравен обратной величине индекса цен J_p, т.е.

J_n=1/J_P (45)

Напомним, что индекс ценпоказывает, во сколько раз выросли цены за рассматриваемый промежуток времени.

4.1. Наращение по простым процентам. Если наращенная за п лет сумма денег составляет S, а индекс цен равен J_p, то реально наращенная сумма денег с учетом их покупательной способности равна

C=S/J_P. (46)

Пусть ожидаемый средний годовой темп инфляции (характеризующий прирост цен за год) равен h. Тогда годовой индекс цен составит (1 + h).

Если наращение производится по простой ставкев течение п лет, то реальное наращение при темпе инфляции h составит

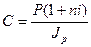(47)

Тогда в общем случае

J_P = 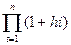(48)

и, в частности, при неизменном h

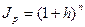(49)

Процентная ставка, которая при начислении простых процентов компенсирует инфляцию, равна

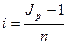(50)

Один из способов компенсации обесценения денег заключается в увеличении ставки процентов на величину так называемой инфляционной премии.Скорректированная таким образом ставка называется брутто-ставкойи обозначается символом r. Брутто-ставка определяется с учетом равенства скорректированного на инфляцию множителя наращения по брутто-ставке множителю наращения по реальной ставке процента

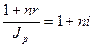(51)

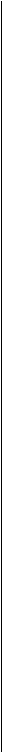откуда

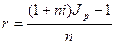(52)

4.2. Наращение по сложным процентам. Наращенная по сложным процентам сумма к концу срока ссуды с учетом падения покупательной способности денег (т.е. в неизменных рублях) составит

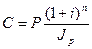(53)

где индекс цен определяется выражением (48) или (49) в зависимости от непостоянства или постоянства темпа инфляции.

Применяются два способа компенсации потерь от снижения покупательной способности денег при начислении сложных процентов.

1. Корректировка ставки процентов, по которой производится наращение, на величину инфляционной премии.Считая, что годовой темп инфляции равен h, можем написать равенство соответствующих множителей наращения с учетом брутто-ставки r:

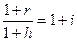, (54)

где i — реальная ставка. Отсюда

r=i+h+ih, (55)

т.е. инфляционная премия равна h+ih.

2. Индексация первоначальной суммы Р. В этом случае сумма Р корректируется согласно движению заранее оговоренного индекса J_p. Тогда

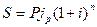. (56)

Как видно, в обоих случаях компенсации потерь от снижения покупательской способности, мы приходим к одной и той же формуле наращения (56). В ней первые два сомножителя в правой части отражают индексацию первоначальной суммы, а если множитель 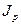отнести к 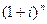, то получим корректировку ставки процента.

4.3. Измерение реальной ставки процента.На практике приходится решать и обратную задачу — находить реальную ставку процента в условиях инфляции. Из тех же соотношений между множителями наращения нетрудно вывести формулы, определяющие реальную ставку /по заданной (или объявленной) брутто-ставке r.

При начислении простых процентов годовая реальная ставка процентов

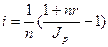(57)

При начислении сложных процентов реальная ставка процентов определяется следующим выражением:

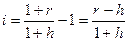(58)

Задания

1. Банк выдает ссуду на 10 лет или под 7% годовых (сложных), или под простые проценты. Какую ставку простых процентов должен установить банк, чтобы полученный им доход не изменился?

2. Банк выдает ссуду на 10 лет под 7% простых годовых. Какую ставку сложных процентов должен установить банк, чтобы полученный им доход не изменился?

3. Определить ставку сложных процентов i_c, эквивалентную ставке а) j₂=10%, б) j₆=10%, в) j₁₂=10%.

4. Банк выплачивает на вложенные в него деньги 8% годовых (сложных). Какую ставку j_m должен установить банк, чтобы доходы клиентов не изменились, если а) m=2, б) m=6, в) m=12?

5. Банк начисляет на вложенные в него деньги проценты по ставке j₄=6% и собирается перейти к непрерывному начислению процентов. Какую силу роста должен установить банк, чтобы доходы клиентов не изменились?

6. Банк учитывает вексель за 60 дней до срока его оплаты по простой учетной ставке d_п=6%. Какую сложную учетную ставку должен установить банк, чтобы доход банка не изменился?

7. Банк учитывает вексель по учетной ставке f₃=8% и желает перейти к сложной учетной ставке dc. Какой величины должна быть ставка d_c, чтобы доход банка не изменился?

8. Банк учитывает векселя по сложной учетной ставке d_с=6%. По какой учетной ставке f_m этот банк должен учитывать векселя, чтобы доход банка не изменился, если а) m=2, б) m=4, в) m=12?

9. Банк выплачивает по вкладам 6% годовых (сложных). Какова реальная доходность вкладов в этот банк, если начисление процентов делается а) по полугодиям, б) поквартально, в) ежемесячно?

10. Банк учитывает векселя по сложной учетной ставке 8%. Какова реальная доходность этой операции?

11. Банк учитывает векселя по сложной учетной ставке f₄=8%. Какова реальная доходность этой операции?

12. В рассматриваемый год ожидаемая инфляция составляет 20%. Какую номинальную годовую процентную ставку следует установить по вкладам в банке, чтобы реальная годовая ставка равнялась 3%?

13. В рассматриваемый год ожидаемая инфляция составляет 20%. Какова реальная доходность по вкладу в банк, если годовой процент по нему равен 25%?

14. Вы разместили имеющуюся денежную сумму в размере 10 млн.руб. в банке под 20% годовых. Через год Вы получили 11,2 млн.руб. Оцените насколько выгодно были размещены Ваши средства, если темпы инфляции за этот период времени составили 22%.

15. Вы планируете через год купить новый автомобиль, текущая цена которого составляет 360 тыс.руб. Годовая ставка банковского процента равна 10%. Ожидаемый уровень инфляции – 5%. Какую сумму денег Вам следует положить сегодня в банк, чтобы при указанных условиях Вы смогли купить новый автомобиль через год?

16. В банк помещена на год сумма 5 тыс.руб. По истечении года клиент получает в банке 7 тыс.руб. Цены в течение года выросли на 50%. Определите процентный доход, номинальную и реальную процентные ставки.