Погашение долга равными срочными уплатами

Расходы должника при расчете по этому методу постоянны на протяжении всего срока погашения долга. Обозначим через A- сумму долга, Y- срочная уплата, I_k - проценты по займу, R_k - расходы по погашению основного долга (k - номер периода погашения). Тогда очевидно, что

Y = I _k + R _k

При этом остаток основного долга и суммы процентных платежей уменьшаются от периода к периоду, R_k- увеличиваются. Срочные уплаты являются обычными рентами. Если задан срок погашения n, то легко находим величину срочной уплаты Y. Для этого приравняем сумму долга A к современной величине ренты (см. формулу (17)).

Y = A / a(n;i), (22)

где a(n;i) -коэффициент приведения годовой ренты со ставкой процентаi и сроком n.

Пример.Банк выдал долгосрочный кредит в сумме 4 млн. руб. на 5 лет под 6% годовых. Погашение кредита должно производиться равными ежегодными выплатами в конце каждого года, включающими погашение основного долга и процентные платежи. Проценты начисляются раз в год. Определите величину ежегодной выплаты.

Решение. Здесь A = 4 млн. руб., n = 5 лет, i = 0,06. По формуле (22) находим величину ежегодной выплаты:

Y = 4 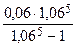= 949 600 руб.

Планирование страхового (погасительного) фонда

В финансовой практике встречаются ситуации, когда кредитный контракт предусматривает выплату займа разовым платежом. В этом случае, особенно при значительных размерах кредита, заемщик для своевременного погашения долга создает страховой фонд.

Рассмотрим планирование фонда с постоянными срочными взносами. Пусть создание страхового фонда производится путем внесения в банк ежегодных взносов R, на которые начисляются сложные проценты по ставке i. Одновременно происходит начисление процентов на величину долга по простой ставке g. В этом случае срочная уплата составит:

Y = Ag + R, (23)

где A - величина долга. Найдем величину R. Поскольку фонд должен быть накоплен за n лет, то взносы образуют обычную ренту с параметрами R, n, i (см. п. 5 ). Так как накопленная сумма (наращенная сумма ренты) должна быть равна величине основного долга A, то A= R×s(n;i). Тогда величина ежегодного взноса равна:

R = A / s(n;i).

Подставляя это значение в (23), получим:

Y = A g + A / s(n;i), (24)

т.е. в фонд систематически вносится сумма, равная R = A / s(n;i). Если условия контракта предусматривают присоединение процентов к сумме основного долга, то срочная уплата определяется следующим образом:

Y = A (1 + g) ⁿ / s(n;i).

Накопленные за k лет средства фонда определяются по формулам наращенных сумм обычных рент или рекуррентно:

S_k+1 = S _k (1 + i) + R. (25)

Пример. Фирма получила кредит 50 млн. руб. на 4 года под 8% годовых в банке А. Погашение долга производится разовым платежом. Одновременно с получением кредита фирма начала создавать страховой фонд, открыв счет в банке Б, где на взносы начисляются 10% годовых. Определите ежегодные расходы фирмы по амортизации долга при условии, что в погасительный фонд вносятся ежегодно равные суммы.

Решение. Параметры финансовой операции:

A = 50,0; g = 8 %; i = 10 %; n = 4, s(4;0,1) = 4,6410;

Находим величину ежегодных взносов в страховой фонд:

R = 50/ 4,6410 = 10,7735 млн. руб.

Процентные платежи по долгу I = A × g = 50 × 0,08 = 4 млн руб. Накопления на конец года в фонде (для банка Б) рассчитаем по формуле (25):

S₁ = R = 10,7735 млн. руб. (S ₀ = 0),

S₂ = 10,7735 × 1,1 + 10,7735 = 22,6244 млн руб.

S₃ = 22,6244 × 1,1 + 10,7735 = 35,6603 млн руб.

S₄ = 35,6603 × 1,1 + 10,7735 = 49,9998 » 50,0 млн руб.

План погашения представим в виде таблицы:

год	I	R	S k	Y k
	4,0000	10,7735	10,7735	14,7735
	4,0000	10,7735	22,6244	14,7735
	4,0000	10,7735	35,6603	14,7735
	4,0000	10,7735	49,9998	14,7735
Итого	16,0000	43,0940	-	59,0940

В данной ситуации фирма-заемщик сумела с выгодой для себя реализовать кредитную операцию, т.к. i>g. В результате общая сумма расходов по погашению долга составила 59,0940 млн руб., что значительно меньше, чем, если бы фирма погасила долг разовым платежом. Экономия составила:

DD = 50 ( 1 + 0,08 × 4 ) - 59,0940 = 6,9060 млн. руб.

Замечание: более сложные схемы погашения долга см. в [1], [3].

Погашение ипотечной ссуды

Ипотечную ссуду выдают под залог имущества (земли, дома и т.п.) на длительный срок. В случае невозврата ссуды в установленный срок заложенное имущество становится собственностью кредитора. Здесь мы рассмотрим традиционную ипотечную ссуду, которая погашается равными ежемесячными выплатами и на которые также ежемесячно начисляются проценты.

Пусть размер ссуды D, выдана она на срок n лет под годовую ставку сложных процентов i. Равные ежемесячные выплаты размером R образуют ренту с частотой платежей и начислением процентов 12 раз в году. Ее наращенная сумма к концу k-го года составит R×s(12k, i/12) и для определения R имеем уравнение

R s(12n, i/12) = D(1+i/12)¹²ⁿ ,

где n - срок ипотечной ссуды. Легко определить на конец любого года остаток, который еще предстоит выплатить. Определим остаток R_k на конец k-го года. К концу k-го года наращенная величина ссуды есть D(1+i/12)^12k, а наращенная величина выплат ренты равна R×s(12k,i/12). Значит остаток R_k = =D(1+i/12) ^12k - R× s(12k, i/12).

Пример.Пусть ссуда в $100 000 выдана на 10 лет под 3 % годовых. Определим ежемесячную выплату и остаток к концу 5-го года.

Решение. Определяем величину коэффициента s(120, 3/12), (например, с помощью компьютерной программы Mathcad):

s(120, 3/12) = [(1+ 0,0025)¹²⁰ - 1]/0,0025 = 139,74.

Ежемесячную выплату вычислим по формуле (26):

R = 100000 ×1,162/139,74 = 831,544.

Определим теперь остаток к концу 5 - го года. Наращенная величина ссуды к этому моменту равна 100000× (1+ 0,0025)⁶⁰ = 116 200. Наращенная величина произведенных выплат есть

715,61×S(60; 0,25) = 864,647,

следовательно, остаток к концу 5- го года равен

R₅ = 864,647 - 831,544 = 33,103.

Задачи

6.1Долг в сумме 1000 тыс. руб. необходимо погасить равными срочными уплатами в течение 5 лет. За заем выплачиваются проценты по ставке 10 % годовых. Определите величину ежегодной выплаты.

6.2Долг в размере 100 тыс. руб. получен под 8 % годовых на 4 года. Одновременно с получением ссуды для ее погашения создан страховой фонд, в который делаются равные ежегодные взносы, На деньги, внесенные в фонд, выплачиваются 5 % годовых. Найдите ежегодную срочную уплату по долгу.Ответ:31201,18 руб.

6.3 Фермер взял в банке 500 тыс. руб. под 10 % годовых на 5 лет. Для погашения долга он образовал страховой фонд, внося в него равные ежегодные взносы и получая на эти деньги 10 % годовых. Найдите ежегодную срочную уплату по долгу.

6.4 Решите предыдущую задачу при условии, что на деньги, вкладываемые в страховой фонд, начисляются 8 % годовых.

6.5 Владелец магазина получил в банке ссуду $20 000 сроком на 4 года. Банковская процентная ставка 10 % годовых. Для погашения ссуды владелец магазина создал страховой фонд, внося в него равные ежегодные взносы и получая на эти деньги проценты по ставке j₄=5 %. Какова ежегодная срочная уплата по долгу?