Коэффициент концентрации доходов Джини
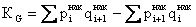 ,
,
где 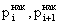 - накопленные (кумулятивные) итоги доли численности населения в i-ой группе (i+1 группе),
- накопленные (кумулятивные) итоги доли численности населения в i-ой группе (i+1 группе),
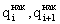 накопленные (кумулятивные) итоги доли объема денежных доходов в i-ой группе (i+1 группе).
накопленные (кумулятивные) итоги доли объема денежных доходов в i-ой группе (i+1 группе).
Чем ближе КG к 1, тем уровень неравенства (концентрации) выше, чем ближе к 0, тем уровень равенства выше.
Обобщающие показатели уровня жизни населения
Наиболее известным показателем, обобщающим характеристики уровня жизни населения, является индекс развития человеческого потенциала (ИРЧП).Он включает в себя три показателя, отражающие наиболее важные аспекты уровня жизни:
- ожидаемую продолжительность жизни при рождении;
-достигнутый уровень образования,
-реальный объем ВВП в расчете на душу населения в паритетах покупательной способности валют.
ИРЧП рассчитывается как средняя арифметическая простая индексов трех указанных показателей: ИРЧП 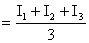 .
.
Индекс каждого показателя рассчитывается по формуле: 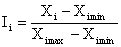 ,
,
где Xi – фактическое значение i – го показателя,
Xi min и Xi max - соответственно минимальное и максимальное значение i-го показателя.
Для расчета индекса ожидаемой продолжительности жизни при рождении(I1) в качестве минимального и максимального значения принимают 25 и 85 лет:
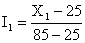 ,
,
Индекс достигнутого уровня образования – это средняя арифметическая взвешенная из двух субиндексов: индекса грамотности взрослого населения (I2(1)) весом 2/3 и индекса совокупной доли учащихся начальных, средних и высших учебных заведений (I2(2)) весом 1/3 :
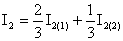
При исчислении грамотности среди взрослого населения (в возрасте от 25 лет и старше) Xi min принимается равным 0, а Xi max =100. Индекс совокупной доли учащихся рассчитывается для лиц моложе 25 лет, а предельные значения доли принимаются такие же, как и а индексе грамотности (0 и 100%).
Индекс реального ВВП на душу населения рассчитывается исходя из принятых минимального и максимального значений 100 и 40000 долл. по ППС:
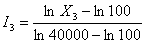
ИРЧП меняется в пределах от 0 до 1. Чем ближе значения к 1, тем выше развитие человеческого потенциала. К странам с высоким уровнем развития, относятся страны, у которых ИРЧП не меньше 0,8, для стран с низким уровнем развития ИРЧП не превышает 0,5, для стран со средним уровнем развития ИРЧП находится в диапазоне от 0,5 до 0,8.
Расчет перспективной численности населения
Если известна численность населения на начало периода и определен коэффициент общего прироста населения, перспективную численность можно определить по формуле:
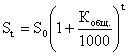 ,
,
где St – перспективная численность населения через t лет,
S0 – исходная численность населения,
Кобщ. – коэффициент общего прироста населения (в промилле).
Пример 1:
Движение населения области за год характеризуется следующими данными, тыс. чел.:
Численность населения на начало года (Нн.г.) 4200,
в том числе женщин в возрасте от 15 до 49 лет (Ж15-49 к.г.) 1460,
Численность населения на конец года (Нк.г.) 4600,
в том числе женщин в возрасте от 15 до 49 лет (Ж15-49 к.г.) 1500,
В течение года:
-родилось (Р) 37,
-умерло (М) 60,
-умерло детей до года 0,67.
Определить:
1. Среднегодовую численность населения и в том числе женщин в возрасте от 15 до 49 лет,
2. Общие и частные коэффициенты естественного воспроизводства населения.
Решение:
1. 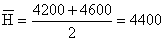 тыс. чел.,
тыс. чел.,
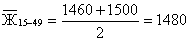 тыс. чел.,
тыс. чел.,
2. Коэффициент рождаемости 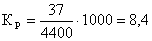 ,
,
Коэффициент смертности 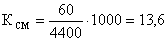 ,
,
Коэффициент естественного прироста (убыли) населения 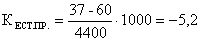 ,
,
что означает убыль на каждые 1000 человек,
Коэффициент фертильности 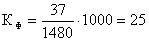 ,
,
Коэффициент младенческой смертности 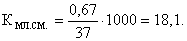
Пример 2:
Определите, в какой стране дифференциация населения по доходу выше, вычислив коэффициенты концентрации Лоренца и Джини.
| Группы населения по уровню среднедушевого дохода | Численность населения, % к итогу | Доля общего дохода по группам, % к итогу в стране | Накопленные итоги | |||
| А | В | Доли численности населения | Доли общего дохода в стране | |||
| А | В | |||||
| pi | qi (А) | qi (В) | 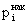 | 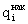 (А) (А) | 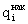 (В) (В) | |
| 1 с наименьшими 2 3 4 5 с наивысшими | 20 20 20 20 20 | 10,4 15,2 19,1 23,8 31,5 | 8,0 13,3 18,1 24,5 36,1 | 20 40 60 80 100 | 10,4 25,6 44,7 68,5 100 | 8,0 21,3 39,4 63,9 100 |
| Итого | 100 | 100 | 100 | Х | Х | Х |
Коэффициенты Лоренца:
-В стране «А»:
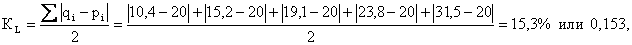 -В стране «В»:
-В стране «В»:
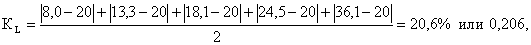
Коэффициенты Джини: 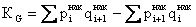
-В стране «А»:
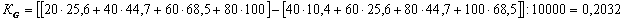
-В стране «В»:
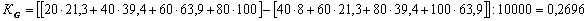
Уровень концентрации доходов (неравенства) выше в стране «В».
Тема 8: Статистика кредита
Кредит– это разновидность экономической сделки, договор между юридическими и физическими лицами о займе или ссуде. Один из партнеров (кредитор) представляет другому (заемщику) деньги (в некоторых случаях имущество) на определенный срок с условием возврата эквивалентной стоимости, как правило, с оплатой этой услуги в виде процента.
Система показателей статистики кредита
Представление об эффективности государственных кредитных операций дает показатель, который характеризует процентное отношение суммы превышения поступлений над расходами по системе государственного кредита. Вычисляется по формуле:
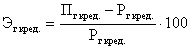
Где 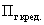 -поступления по системе государственного кредита;
-поступления по системе государственного кредита;
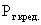 - расходы по системе государственного кредита.
- расходы по системе государственного кредита.
Среди обобщающих показателей кредита статистика широко применяет средние и относительные величины кредитования и расчетов: среднегодовой объем кредита, средний объем выданной суммы, средний срок ссуды, среднее число оборотов кредита за год и др.
Так как учет кредитных вложений ведется на начало периода, средний объем кредитных вложений исчисляется по средней хронологической.
Средний размер кредита (ссуды)вычисляется по формуле средней арифметической взвешенной (без учета числа оборотов в год):
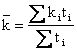
Где 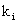 - размер i-ой ссуды;
- размер i-ой ссуды;
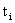 - срок i-ой ссуды.
- срок i-ой ссуды.
Средний срок пользования ссудами – это время, в течение которого все ссуды оборачиваются один раз при условии их непрерывной оборачиваемости, вычисляется:
1) по формуле средней арифметической взвешенной (при этом весами являются размеры выданных ссуд:
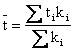
2) по формуле средней гармонической взвешенной (когда вместо размеров ссуд известна продолжительность оборота каждой ссуды):

Среднее число оборотов ссуд за годопределяется по формуле:

Где 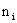 - число оборотов i – ой ссуды за год;
- число оборотов i – ой ссуды за год;
Д – число дней (месяцев в году).
За пользованием кредита взимается плата в размере процентных ставок. Средняя процентная годовая ставка кредитарассчитывается по формуле:
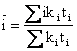
Где i – годовая ставка i – ой ссуды;
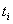 - срок i – ой ссуды (в годах).
- срок i – ой ссуды (в годах).
Изучение просроченных ссуд:
абсолютная сумма просроченных кредитов:
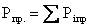 ;
;
относительные показатели просроченной задолженности по ссудам:
-
по сумме 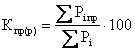 ;
;
- по сроку 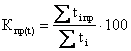
Где 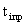 - число просроченных дней по погашению I – го кредита;
- число просроченных дней по погашению I – го кредита;
- по сумме и сроку (интегральный средневзвешенный показатель просроченной задолженности):
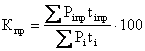 .
.
Пример 1
Коммерческий банк выдал в течение года 5 кредитов:
| № кредита | 1 | 2 | 3 | 4 | 5 |
| Размер кредита, тыс. руб. k | 400 | 950 | 760 | 800 | 1200 |
| Срок кредита, мес. t | 8 | 6 | 2 | 4 | 7 |
Определить: 1) средний размер кредита;
2) средний срок пользования ссудами (при условии их непрерывной оборачиваемости);
3) среднее число оборотов ссуд за год.
Составим вспомогательную таблицу:
| № ссуды | Размер ссуды, тыс. руб. k | Срок ссуды, мес. t | Число оборотов за год 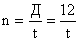 | Годовой оборот 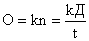 | 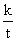 | 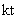 |
| 1 2 3 4 5 Итого | 400 950 760 800 1200 4110 | 8 6 2 4 7 27 | 1,5 2,0 6,0 3,0 1,7 - | 600 1900 4560 2400 2040 11500 | 50,0 158,3 380,0 200,0 171,4 959,7 | 3200 5700 1520 3200 8400 22020 |
Средний размер ссуды: 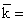 22020/27=815,6 тыс. руб.
22020/27=815,6 тыс. руб.
Средний срок пользования кредитами: 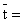 4110 / 959,7=4,28 мес.
4110 / 959,7=4,28 мес.
Среднее число оборотов ссуд: 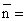 11500 / 4110=2,8 оборота,
11500 / 4110=2,8 оборота, 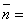 12/4,28=2,8 оборота.
12/4,28=2,8 оборота.
Пример 2
Имеются следующие данные:
| Сумма кредита (k), тыс. руб. | Срок кредита (t), мес. | Годовая процентная ставка (i) |
| 300 700 | 6 4 | 20 15 |
Определить среднюю процентную ставку.
Составим вспомогательную таблицу:
| k | t, лет | i | kt | ikt |
| 300 700 Итого | 0,50 0,33 - | 0,20 0,15 - | 150 105 255 | 30,00 15,75 45,75 |
Средняя процентная ставка по двум кредитам равна:
i = (45,75 / 255)·100=17,94%.
Пример 3
Имеются следующие данные по банку:
| Заемщик | 2005 г. | На 1 января 2006 г. | ||
| Сумма выданных кредитов, тыс. руб. | Срок, дни | Просроченная задолженность, тыс. руб. | Число просроченных дней | |
| 1 2 3 | 900 1500 300 | 10 250 50 | 50 25 - | 3 10 - |
По состоянию на конец года по банку в целом определить:
1) абсолютную сумму просроченных кредитов;
2) относительные показатели просроченной задолженности по ссудам.
Решение:
1) абсолютная сумма просроченных кредитов равна 50 + 25 = 75 тыс. руб.;
2) относительные показатели просроченной задолженности:
а) по сумме: 75 / (900 + 1500 + 300) · 100 = 2,78%;
б) по сроку: (3 + 10) / (10 + 250 + 50) · 100 = 4,19%;
в) по сумме и сроку: (50 · 3 + 25 · 10) / (900 · 10 + 1500 · 250 + 300 · 50) · 100 = 400 / 399000 · 100 = 0,10%.
Тема 9: Статистика страхования
Страхование представляет собой систему экономических отношений, которая включает образование специального фонда (страхового фонда) и его использование (распределение и перераспределение) для преодоления и возмещения разного рода потерь, ущерба, вызванных неблагоприятными событиями (страховыми случаями) путем выплаты страхового возмещения и страховых сумм.
Виды страхования
1) Имущественное страхование представляет собой вид страхования, объектом которого выступают материальные ценности. Осуществляется на случай пожара, аварии, порчи, хищения и т.п.
2) Личное, в котором объектом страховых отношений выступают имущественные интересы, связанные с жизнью, здоровьем, трудоспособностью и др.
3) Страхование ответственности – вид страхования, объектом которого выступает обязанность страхователей выплатить какие – либо договорные условия, либо обязанность страхователей по возмещению материального или иного ущерба;
4) Социальное страхование представляет собой специальный вид страхования с целью материального обеспечения нетрудоспособных граждан в результате болезни, несчастного случая, рождения ребенка, а также других обстоятельств.
Система статистических показателей имущественного страхования
Абсолютные показатели:
1) Страховое поле (Nmax
).
2) Общая численность застрахованных объектов или заключенных договоров – страховой портфель (N).
3) Число страховых случаев (nc).
4) Число пострадавших объектов (n
П).
5) Страховая сумма застрахованных объектов (S).
6) Страховая сумма пострадавших объектов (S
п).
7) Сумма поступивших страховых платежей (V).
8) Сумма выплат страхового возмещения (W).
Средние показатели:
1) Средняя страховая сумма застрахованных объектов: 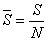 .
.
2) Средняя страховая сумма пострадавших объектов: 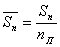 .
.
3) Средний размер выплаченного страхового возмещения: 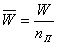 .
.
4) Средний размер страхового платежа (взноса): 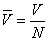 .
.
Относительные показатели:
1) Степень охвата страхового поля: 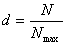 .
.
2) Степень охвата объектов добровольным страхованием: 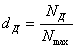 ,
,
где N
Д – количество застрахованных объектов в добровольном порядке.
Данный показатель характеризует уровень развития добровольного страхования.
3) Доля пострадавших объектов: 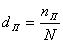 .
.
Этот показатель определяет удельный вес объектов, которые были повреждены в отчетном периоде.
4) Частота страховых случаев: 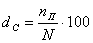 .
.
Показывает, сколько страховых случаев приходится на 100 застрахованных объектов, т.е. заключенных договоров.
5) Уровень опустошительности страховых случаев: 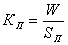 .
.
Характеризует удельный вес суммы возмещения страховой суммы пострадавших объектов. Его предельное значение не превышает 1.
6) Коэффициент выплат страхового возмещения: 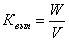 .
.
Определяет размер выплат страхового возмещения на 1 (100) руб. поступивших страховых платежей и может быть использован для анализа финансового состояния страховых компаний. Страховое учреждение будет тем рентабельнее, чем меньше будет значение этого показателя.
7) Абсолютная сумма дохода страховых компаний: 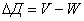 .
.
8) Относительная доходность или процент дохода страховых организаций: 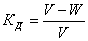 .
.
9) Уровень взносов по отношению к страховой сумме: 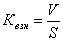 .
.
Этот показатель характеризует размер взноса страховых платежей на 1 (100) руб. страховой суммы. Представляет собой сложившуюся усредненную ставку страховых платежей по всем видам застрахованного имущества.
Пример 1:
Имеются условные данные о добровольном страховании имущества граждан:
Страховое поле (Nmax) – 250000;
Общая численность застрахованных объектов (N) – 100500;
Число пострадавших объектов (n
П) – 2100;
Страховая сумма застрахованного имущества (S), млн. руб. – 19500;
Страховая сумма пострадавших объектов (S
п).
Сумма поступивших страховых платежей (V), млн. руб. – 280;
Сумма выплат страхового возмещения (W), млн. руб. – 160.
Определить показатели, характеризующие деятельность страховых организаций.
Решение:
1) Степень охвата страхового поля: 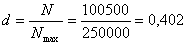 или 40,2%.
или 40,2%.
2) Частота страховых случаев: 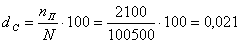 , или 2,1%.
, или 2,1%.
То есть 2,1 страховых случая приходится на 100 застрахованных объектов, т.е. заключенных договоров.
3) Средняя страховая сумма: 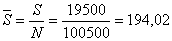 тыс. руб.
тыс. руб.
4) Средний размер страхового платежа (взноса): 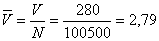 тыс. руб.
тыс. руб.
5) Средний размер выплаченного страхового возмещения: 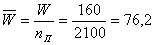 тыс. руб.
тыс. руб.
6) Коэффициент выплат страхового возмещения: 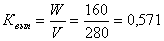 , или 57,1%.
, или 57,1%.
7) Уровень убыточности страховых сумм: 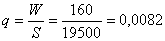 .
.
8) Коэффициент тяжести страховых событий: 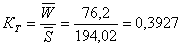 или 39,27%.
или 39,27%.
9) Коэффициент финансовой устойчивости (с доверительной вероятностью 0,954, при которой табличное значение t = 2): 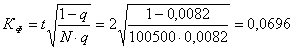 .
.
Пример 2:
Имеются условные данные о результатах работы страховых организаций:
| № организации | Страховой взнос, млн. руб., V | Коэффициент выплат, КВ | Выплаты W = КВ V |
| 1 2 3 | 400 500 700 | 0,5 0,6 0,2 | 200 300 140 |
| Итого | 1600 | - | 640 |
Определить:
1) Средний коэффициент выплат;
2) Абсолютную сумму дохода;
3) Относительную доходность.
Решение:
1) Коэффициент выплат вычисляется по формуле: 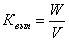 .
.
Средний коэффициент выплат составит: 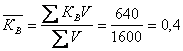 , или 40%.
, или 40%.
2) Абсолютная сумма дохода определяется разностью взносов и выплат: 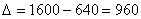 млн. руб.
млн. руб.
3) Относительная доходность или процент дохода страховых организаций: 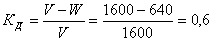 или 60%.
или 60%.
Тема 10: Статистика цен и инфляции
Цена – это сумма денег, уплачиваемая за единицу товара, эквивалент обмена товара на деньги.
Методы расчета уровня цен
Уровень цен – обобщающий показатель, характеризующий состояние цен за определенный период времени, на определенной территории, по совокупности товаров и товарных видов с близкими потребительскими свойствами.
Индивидуальный уровень цены – это абсолютная величина – сумма денег, уплачиваемых на рынке за товарную единицу. Для цен совокупности однородных товарных единиц, для цен, варьирующих во времени и пространстве, обобщенной характеристикой является средний уровень цен.
Для расчета средних цен используются следующие виды средних величин:
1. Средняя арифметическая взвешенная рассчитывается по формуле:
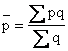
Где p – цена единицы товара; q – количество товара.
2. Средняя гармоническая взвешенная определяется по формуле:
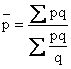
Где pq – товарооборот в денежном выражении.
3. Средняя хронологическая простая исчисляется по формуле:
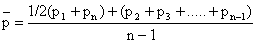
Где n
– число месяцев в периоде.
Она применяется в том случае, если моменты регистрации равноудалены друг от друга.
4. Средняя хронологическая взвешенная рассчитывается по формуле:
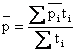
Где 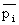 - средняя цена за период; ti – продолжительность периода.
- средняя цена за период; ti – продолжительность периода.
Она применяется в том случае, если моменты регистрации удалены друг от друга на разные величины.
Система индексов цен
Индекс цен – относительный показатель, выраженный в коэффициентах или процентах, характеризующий изменение цен во времени (индекс динамики) или пространстве (территориальный индекс).
I
. Индивидуальные (частные) индексы. Характеризуют динамику цен конкретного продукта:
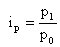
Где p
1
и
p
0 – цены единицы товара в текущем и базисном периодах.
Средняя арифметическая из частных индексов. Предложен итальянским экономистом Д.Р.Карли (1752):
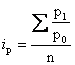
Где n – число индексов.
Индивидуальный индекс средних цен. Характеризует динамику средней цены товара. Применяется при изучении динамики цен товарных групп, цен одного товара по различным территориям и субрынкам.
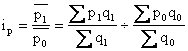
II
. Агрегатные, средние арифметические и средние гармонические взвешенные индексы цен.
Индекс Этьена Ласпейреса (1871).


Индекс Германа Пааше (1874).

Индекс цен Ласпейреса, как правило, больше индекса цен Пааше. Эта систематическая зависимость двух индексов известна как эффект Гершенкрона.
Индекс Джозефа Лоу (1822). Соизмеритель индексируемых величин 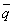 ; применяется в расчетах при реализации товаров в течение продолжительных периодах времени (пятилетках, десятилетий и т.д.).
; применяется в расчетах при реализации товаров в течение продолжительных периодах времени (пятилетках, десятилетий и т.д.).
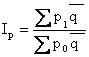
Где 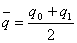 - средняя (невзвешенная) величина реализации за два или большее число периодов.
- средняя (невзвешенная) величина реализации за два или большее число периодов.
III. Геометрическая формула индекса.
Индекс, предложенный Стэнли Джевонсом (1863). Корень степени n из произведения индивидуальных индексов.
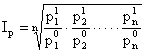
Где 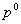 и
и 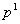 - цены базисного и текущего года различных товаров; n – число товаров.
- цены базисного и текущего года различных товаров; n – число товаров.
«Идеальный» индекс Ирвине Фишера (1927). Представляет среднюю геометрическую невзвешенную произведения индексов Ласпейреса и Пааше.

IV. Территориальные индексы. В сводных индексах цен в качестве индексируемых величин могут приниматься количества проданных товаров разных регионов 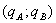 или сумма реализованных товаров по двум регионам
или сумма реализованных товаров по двум регионам 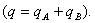 Выбор базы сравнения (региона) и весов – соизмерителей определяется целями исследования.
Выбор базы сравнения (региона) и весов – соизмерителей определяется целями исследования.
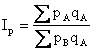 или
или 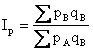 ,
,
или 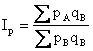 , или
, или 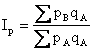
Где 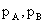 - цены товаров в регионах A и B.
- цены товаров в регионах A и B.
Инфляция – является неотъемлемой категорией любой экономики, которая использует бумажно-денежное обращение. Она представляет собой обесценивание бумажных денег и безналичных денежных средств, сопровождающееся ростом цен на товары и услуги в экономике, падением уровня реальной заработной платы, неудовлетворенностью платежеспособного спроса населения, связанное с нарушением финансирования – это категория, которая обозначает снижение покупательной способности денег.
