ЭР:неоклассическая модель Солоу
Кейнсианские модели роста неплохо описывали реальные процессы в 1920 - 1950 гг., но для последующих периодов более подходящей, как показывает практика, является неоклассическая модель Р. Солоу. (См. подробнее: Гальперин В.М. и др. Макроэкономика: Учебник. Спб., 1994.).
Р. Солоу (Нобелевская премия 1987 г. за разработку факторов экономического роста) показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимозаменяемости факторов производства. Поэтому он в своей модели использует производственную функцию Кобба-Дугласа. Другими предпосылками анализа у него являются: убывающая предельная производительность капитала; постоянная отдача от масштаба, постоянная норма выбытия, отсутствие инвестиционных лагов.
В производственной функции Кобба-Дугласа объем производства (Yt) есть функция от двух факторов - капитала (Kt) и труда (Nt):
Yt = Y (Kt, Nt) = Kta Nt1-a , которые являются хорошими субститутами и сумма коэффициентов эластичности (a ) выпуска по факторам равна единице (постоянная эффективность от масштаба).
Так как параметром, обеспечивающим равновесный рост в модели Солоу, является капиталовооруженность труда, представим производственную функцию в виде:
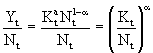
и обозначив 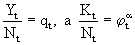 , получим
, получим 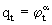 , т.е. в модели Солоу средняя производительность труда есть функция его капиталовооруженности. По мере роста капиталовооруженности труда его производительность увеличивается, но с убывающей скоростью, так как снижается предельная производительность капитала.
, т.е. в модели Солоу средняя производительность труда есть функция его капиталовооруженности. По мере роста капиталовооруженности труда его производительность увеличивается, но с убывающей скоростью, так как снижается предельная производительность капитала.
Функция предложения труда ( 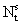 ) в модели Солоу имеет вид:
) в модели Солоу имеет вид:
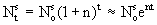 ,
,
где e - основания натуральных логарифмов; n - годовой темп прироста населения и предложения труда, 0 < n < 0,3.
Тогда годовой объем производства и предложения благ представляется такой функцией: Yt = y (Kt, No ent ),
а объем ежегодно используемого капитала - Кt = 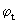 No ent .
No ent .
Чтобы экономический рост был равновесным, нужно чтобы Jt = St или 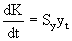 .
.
Определим из предыдущего 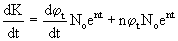
И поэтому получим: 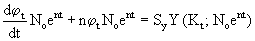 .
.
Так как производственная функция в модели Солоу имеет постоянную отдачу от масштаба, то 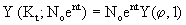 .
.
Принимая также во внимание, что по экономическому смыслу 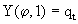 , тогда условие равновесного роста можно представит в таком виде:
, тогда условие равновесного роста можно представит в таком виде: 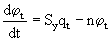 .
.
Это выражение показывает, как во времени должна изменяться капиталовооруженность труда, чтобы равновесный рост, обеспечивающий полное использование производственных мощностей, сопровождался полной занятостью.
Поскольку qt есть доход на одного занятого, то Syqt представляет объем осуществляемых им в период t сбережений. Для равновесного роста нужно, чтобы сбережения были инвестированы. Спрос на инвестиции в период t определяется потребностью в дополнительном капитале для оснащения им вновь нанятых в этом периоде рабочих. Произведение nQt показывает, сколько в среднем требуется дополнительного капитала на одного работающего, чтобы капиталовооруженность вновь привлеченных в период t рабочих равнялась 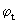 .
.
Следовательно, при 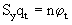 будет происходить равновесный рост с постоянными капиталовооруженностью и производительностью труда. Когда
будет происходить равновесный рост с постоянными капиталовооруженностью и производительностью труда. Когда
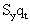 >
> 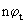 , объем сбережений превышает объем инвестиций, поэтому здесь надо переходить к более капиталоемкой технологии, т.е. повысить
, объем сбережений превышает объем инвестиций, поэтому здесь надо переходить к более капиталоемкой технологии, т.е. повысить 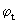 . Соответственно при
. Соответственно при 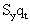 <
< 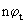 для сохранения равновесия и обеспечения полной занятости (
для сохранения равновесия и обеспечения полной занятости ( 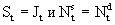 ) приходится снижать капиталовооруженность труда. Неоклассики предполагают, что возможности изменения капиталовооруженности связаны с гибкостью цен на факторы производства, обеспечиваемой конкуренцией на рынке.
) приходится снижать капиталовооруженность труда. Неоклассики предполагают, что возможности изменения капиталовооруженности связаны с гибкостью цен на факторы производства, обеспечиваемой конкуренцией на рынке.
Из этого Солоу выводит и "золотое" правило накопления. В качестве критерия оптимальности принимается максимум потребления на одного занятого: 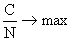 .
.
Эта средняя норма потребления представляется в виде функции капиталовооруженности труда. Так как 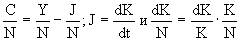 , то
, то 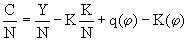 ; средняя норма потребления достигает максимума при
; средняя норма потребления достигает максимума при 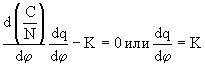 .
.
Следовательно, средняя норма потребления достигает максимума, когда темп прироста капитала равен предельной производительности капитала. Сформулированное в такой форме условие оптимального роста получило название золотого правила накопления.
В последующем Солоу и его последователи рассмотрели в качестве частных случаев данную модель при переменных параметрах роста населения, изменениях технического прогресса, а значит капиталовооруженности труда и изменениях нормы сбережений.
Из неоклассической модели Солоу следует, что в условиях совершенной конкуренции при любой норме сбережений рыночная экономика тяготеет к сбалансированному росту, при котором национальный доход и капитал увеличиваются с темпом, равным темпу роста предложения труда. Однако, следует иметь в виду, что стабильность динамического равновесия в модели Солоу основывается на сравнительно простой производственной функции (Кобба-Дугласа), и при использовании других производственных функций возможности динамического равновесия могут расцениваться совсем по-другому.
Вопрос 60
«Золотое правило» накопления
Примем в качестве критерия оптимальности максимум потребления на одного занятого в каждом периоде: C/N 

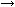 max и определим ее зависимость от капиталовооруженности труда. С учетом равенств
max и определим ее зависимость от капиталовооруженности труда. С учетом равенств
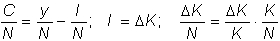 | . |
среднюю норму потребления можно представить в виде
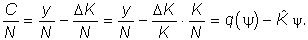 |
Она достигает максимума при
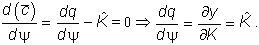 |
Таким образом, объем потребления на одного работающего достигает максимума, когда темп прироста капитала равен его предельной производительности.
Для определения нормы сбережений, максимизирующей среднюю норму потребления в динамическом равновесии, продифференцируем  по s. Так как
по s. Так как
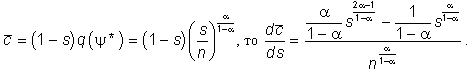 |
Следовательно, средняя норма потребления максимальна при
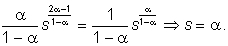 | (14.4) |
Равенство (14.4) представляет «золотое правило» накопления: если норма сбережений равна эластичности выпуска по капиталу, то в растущей с постоянным темпом экономике средняя норма потребления достигает максимума при полном использовании труда и капитала.
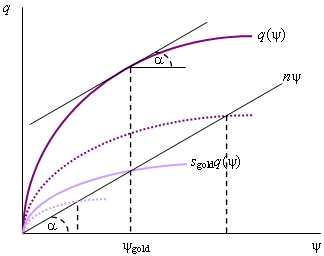
| Так как в условиях совершенной конкуренции доля прибыли в национальном доходе равна эластичности выпуска по капиталу, то из равенства (14.4) следует, что в соответствии с «золотым правилом» вся прибыль должна инвестироваться в реальный капитал. Графический способ определения нормы сбережений, соответствующей «золотому правилу», показан на рис. 14.7. При заданной технологии и фиксированном темпе роста трудовых ресурсов каждой норме сбережений соответствует своя устойчивая капиталовооруженность труда. Чтобы определить, какая s обеспечивает максимум  , нужно к графику производственной функции провести касательную, тангенс угла наклона которой равен n, так как в соответствии с «золотым правилом» , нужно к графику производственной функции провести касательную, тангенс угла наклона которой равен n, так как в соответствии с «золотым правилом» 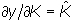 , а при равновесном росте , а при равновесном росте 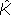 = n. Точка пересечения перпендикуляра, опущенного из точки касания на ось абсцисс, с лучом n = n. Точка пересечения перпендикуляра, опущенного из точки касания на ось абсцисс, с лучом n 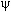 определит оптимальную норму сбережений. Через эту точку должна проходить кривая sq. определит оптимальную норму сбережений. Через эту точку должна проходить кривая sq. |
 Подробней ознакомиться со свойства неоклассической модели экономического роста позволяет
Подробней ознакомиться со свойства неоклассической модели экономического роста позволяет