Понятие и классификация рядов динамики
Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.
Каждый динамический ряд содержит две составляющие:
1) показатели периодов времени (годы, кварталы, месяцы, дни или даты);
2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.
Классификация:
1. По времени:
- моментные – показывает фактическое наличие изучаемого явления в конкретный момент времени;
- интервальный – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени.
2. По форме представления уровней – ряды абсолютных, относительных и средних величин.
3. По расстоянию или интервалам времени между датами выделяют полные или неполные хронологические ряды. В полных рядах дата регистрации или момент времени следуют друг за другом через равные интервалы. Неполные – когда принцип равных интервалов не соблюдается.
4. По числу показателей:
- изолированные, если ведется анализ во времени одного показателя;
- комплексные (многомерные), когда в хронологической последовательности дается система показателей, связанных между собой единством процесса, явления.
Описательные характеристики ряда динамики
| Показатель | Базисный | Цепной | Взаимосвязь |
| Абсолютный прирост |  | 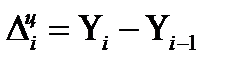 | 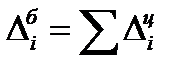 |
| Темп роста |  | 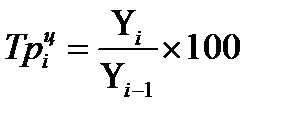 | 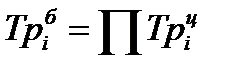 |
| Темп прироста | 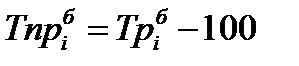 | 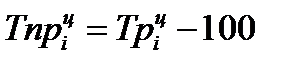 | Проявляется через Тр |
1. Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности.
Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню:
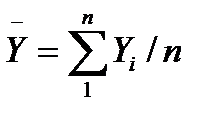 или
или  ,
,
где п или (п+1) – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень.
Если в интервальном временном ряду отрезки времени имеют неравную длительность, то средний уровень рассчитывается по формуле средней арифметической:
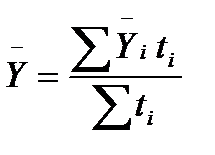 или
или 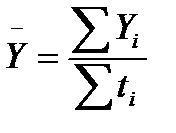 .
.
Для моментного ряда с равноотстоящими моментами используется формула средней хронологической. Вид формулы определяется способом нумерации уровней. Если уровни нумеруются начиная с нуля, то средняя хронологическая имеет вид
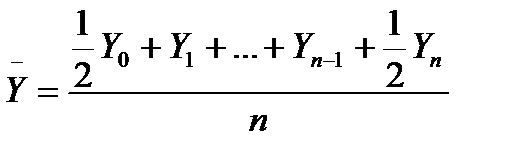 .
.
Средний абсолютный прирост рассчитывается в зависимости от способа нумерации интервалов:
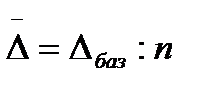 или
или  .
.
3. Средний темп роста:
 .
.
Методы анализа тренда
1. Метод скользящей средней (вычисляется ср. уровень из определенного числа 1х по порядку ур. ряда, затем ср. ур из такого же числа, начиная со 2го значения и т.д.Полученная средняя относится к середине интервала сглаживания)
2. Метод аналитического выравнивания ( предполагает представления ур. ряда динами в виде функции времени, возможно выравнивание по прямой, параболе, линейно-логарифмитеческой ф, показательной ф
Чем ближе к аппроксимации ( R) к 1 тем соответствующая модель наиболее адекватно описывает исходные данные и может быть выбрана для прогнозирования
