ЛАБОРАТОРНАЯ РАБОТА № 6. РАСЧЕТ ЭФФЕКТИВНОСТИ НЕРАВНОМЕРНЫХ КАПИТАЛОВЛОЖЕНИЙ С ПОМОЩЬЮ ФУНКЦИЙ ЧПС, ВСД И ПОДБОР ПАРАМЕТРА
Дисконтирование – метод приведения будущей стоимости денег к их на-стоящей стоимости.
Чистый дисконтированный доход (чистая приведенная стоимость) (англ. Net present value,общепринятое сокращение– NPV (ЧДД)) –это сумма дискон-тированных значений потока платежей, приведенных к сегодняшнему дню.
Иначе говоря, для потока платежей CF, где CFt – платеж через t лет (t = 1, ..., N) и начальной инвестиции в размере IC = −CF0 чистый дисконтиро-ванный доход NPV рассчитывается по формуле:
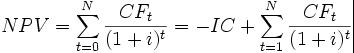
(1)
где i – ставка дисконтирования.
Ставка дисконтирования́ (Дисконтная́ ставка, англ. Discount Rate) – про-центная ставка, используемая для расчета дисконтированной стоимости буду-щих денежных потоков; доходность альтернативных способов инвестирования с такой же степенью риска.
Расчет NPV – стандартный метод оценки эффективности инвестиционно-го проекта, он показывает оценку эффекта от инвестиции, приведенную к на-стоящему моменту времени с учетом разной временной́стоимости денег.
Если NPV больше 0, то инвестиция прибыльна.
Если NPV меньше 0, то инвестиция убыточна.
С помощью NPV можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выго-ден проект с наибольшим NPV).
Положительные качества NPV:
1. Четкие критерии принятия решений.
2. Показатель учитывает стоимость денег во времени (используется коэф-фициент дисконтирования в формулах).
Отрицательные качества NPV:
1. Показатель не учитывает риски.
2. Хотя все денежные потоки являются прогнозными значениями, коэффи-циент дисконтирования может включать в себя инфляцию, однако зачас-тую это всего лишь норма прибыли, которая закладывается в расчетный проект, формула не учитывает вероятность исхода события.
Задание 1
Вас просят дать в долг 10 000 тг.и обещают вернуть через год 2 000 тг., через 2 года – 4 000 тг., через три года – 7 000 тг.При какой про-центной ставке эта сделка выгодна?
Ход решения задачи
Всего Вам собираются отдать 2 000 + 4 000 + 7 000 = 13 000 тг.Это больше, чем те 10 000 тг., которые Вы даете в долг.
Однако стоимость денег сегодня и стоимость тех же денег через один, два или три года различна. Во-первых, надо учитывать инфляционные процессы. Во-вторых, вы могли вложить эти деньги более выгодно – например, положить их в банк под некоторый процент.
Поэтому прежде чем согласиться на дачу займа, необходимо оценить, вы-годно ли это Вам.
Проведем расчеты в MS Excel с помощью встроенной функции листа ЧПС (чистая приведенная стоимость).
Синтаксис функции: ЧПС (ставка; 1-е значение; 2-е значение; ...).
Аргументы:
| Ставка | Процентная ставка за период |
| 1-е значение, 2-е значение, | От 1 до 29 аргументов, представляющих расходы и доходы. Они должны быть равномерно распределены во времени и осуществляться в конце каждого из периодов. Функция использует порядок аргументов для определения порядка поступлений и платежей. |
В приводимом на рис. 44 расчете в ячейку В8 введена формула:
= ЧПС (В7; В3:В5) (2)
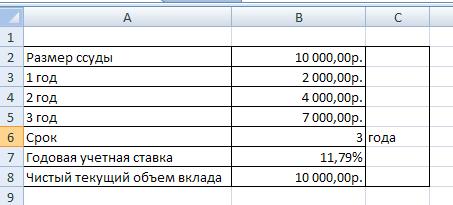
Рис. 44. Расчет годовой процентной ставки
Кроме того, для автоматизации составления таблицы в ячейку С6 введена формула:
=ЕСЛИ(B6=1;"год";ЕСЛИ(И(B6>=2;B6<=4);"года";"лет")) (3)
Нам необходимо найти такое значение годовой учетной ставки, при кото-ром чистый текущий объем вклада будет равен 10 000 тг., то есть размеру ссуды. Сделаем это с помощью средства Подбор параметра.
Первоначально в ячейку В7 вводится произвольный процент, например, 3 %. После этого выбираем:
| для MS Office 2003 | команду Сервис → Подбор параметра | |
| для MS Office 2007 | вкладку на ленте Данные → Анализ «что-если» → Подбор параметров |
Заполняем открывшееся диалоговое окно Подбор параметра, как пока зано на рис. 45.
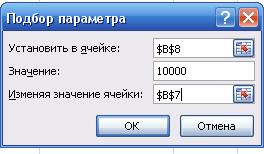
Рис. 45. Диалоговое окно «Подбор параметра» при расчете годовой процентной ставки
В поле Установить в ячейке даем ссылку на ячейку В8, в которой вы-числяется чистый текущий объем вклада поле Значение указываем размер ссуды.
В поле Изменяя значение ячейки даем ссылку на ячейку В7, в которой вычисляется годовая процентная ставка.
После нажатия кнопки ОК средство подбора параметров определит, при
какой годовой процентной ставке чистый текущий объем вклада равен 10 000 тг.В нашем случае годовая учетная ставка равна 11,79 %.
Вывод:если банки предлагают более высокую годовую процентнуюставку, то предлагаемая сделка вам не выгодна.
Можно сделать расчет и другим способом. Функция ЧПС связана с функ-цией ВСД (внутренняя ставка доходности). Внутренняя норма доходности (англ. internal rate of return, общепринятое сокращение – IRR (ВНД)) – это про-центная ставка, при которой чистый дисконтированный доход (NPV) равен 0. NPV рассчитывается на основании потока платежей,дисконтированных к сего-дняшнему дню. Иначе говоря, для потока платежей CF, где CFt – платеж через t лет(t = 1, ..., N)и начальной инвестиции в размере IC = −CF0, внутренняянорма доходности IRR рассчитывается из уравнения:
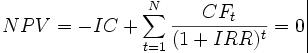 (4)
(4)
или
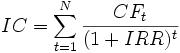 (5)
(5)
Синтаксис: ВСД (значения; прогноз)
Аргументы:
1. Значения – массив или ссылка на ячейки, содержащие числовые величи-ны, для которых вычисляется внутренняя скорость оборота средств. Зна-чения должны содержать по крайней мере одно положительное значение и одно отрицательное значение, для того чтобы можно было вычислить внутреннюю норму доходности.
2. Прогноз – величина, о которой предполагается, что она близка к резуль-тату ВСД.
Для вычислений ВСД MS Excel использует метод итераций. Если функ-ция не может получить результат после 20 попыток, то выдается значение ошибки #ЧИСЛО!
В большинстве случаев нет необходимости задавать прогноз с помощью функции ВСД. Если прогноз опущен, он полагается равным 0,1 (10 %).
Если ВСД выдает значение ошибки или результат далек от ожидаемого, можно попытаться выполнить вычисления еще раз, но уже с другим значением аргумента прогноз.
Задание 2
Самостоятельно решите выше приведенную задачу с помощью использо-вания функции ВСД. Для этого надо изменить знак у одного из числовых пара-метров. Помните: если вы платите деньги, то Excel подразумевает, что это чис-ло отрицательное.
Задания для самостоятельной работы
Вас просят дать в долг Р ден. ед., и обещают вернуть Р1 ден. ед. через год, Р2ден.ед. –через2года и т.д.,наконец Рnден.ед. –через n лет(табл. 3).
При какой годовой процентной ставке эта сделка имеет смысл?
Таблица 3
Варианты для самостоятельной работы
| Вариант | n | P | Р1 | Р2 | Р3 | Р4 | Р5 |
| 170 000 | 5 000 | 7 000 | 8 000 | ||||
| 200 000 | 6 000 | 6 000 | 9 000 | 7 000 | |||
| 220 000 | 5 000 | 8 000 | 8 000 | 7 000 | 5 000 | ||
| 300 000 | 5 000 | 10 000 | 18 000 | ||||
| 350 000 | 5 000 | 9 000 | 10 000 | 18 000 | |||
| 210 000 | 4 000 | 5 000 | 8 000 | 10 000 | 11 000 | ||
| 250 000 | 8 000 | 9 000 | 10 000 | ||||
| 310 000 | 9 000 | 10 000 | 10 000 | 15 000 | |||
| 320 000 | 8 000 | 10 000 | 10 000 | 10 000 | 11 000 | ||
| 360 000 | 10 000 | 15 000 | 21 000 |
