Доходность бескупонной облигации

Получаем из формулы

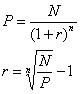
Если надо сравнить доходность по бескупонным облигациям с доходностью купонной облигации, с выплатой дохода m раз в год, то:

Пример:

Цена 600у.е. номинал 1000 до погашения 5 лет. Определить доходность к погашению, если доход выплачивается 1 раз в год.

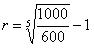
Если инвестор сравнивает доход бескупонной облигации с доходностью купонной облигации с выплатой дохода m раз в год, то используйте такую вот формулу:

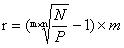
Пример:

P_обл.= 600 у.е.

N = 1000

n = 5

m = 4

r - ?

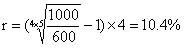
По поводу краткосрочных облигаций предпринимаем вот такие вот действия:

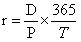, где

D – процентный доход в денежных единицах (величина дисконта, если кто не понял)

Т – число дней до погашения

Если D=N-P

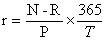
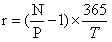
Пример:

N = 1000

Облигация продаётся с дисконтом = 930 у.е.

Т = 50 дней

r – ?

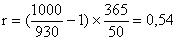
Доходность к погашению очередного купона

И сразу пример, чтобы не расслаблялись:

Облигации с N=1000 по цене 1100. Величина купона = 200, T = 182 дня (продолжительность купонного периода), до выплаты – 91 день. Определить доходность.

D = 1200 – 1100 = 100

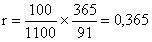
N+величина купонного дохода = 1200

D= N+C-(P_n+А)=1000+200-(1000+100)=100

Методика ЦБ для ОФЗ:

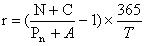
N – номинал

C – величина текущего купона

P_n – чистая цена облигаций (цена в самом начале купонного периода)

А – накопленный доход с начала купонного периода

Т – количество дней до конца купонного периода

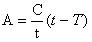
t – продолжительность купонного периода

Вернёмся к примеру:

A = 200/182(182-91)=100

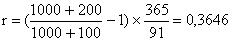
P_n à N

Перепишем:

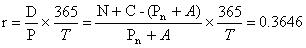
Инвестор может продать облигацию до срока погашения. Тогда необходимо определить доходность за период владения.А делается это вот так вот:

Пример:

Инвестор приобретает бескупонную облигацию за 600 у.е. (а N = 1000), продает через 2 года по цене 800 у.е.

r за период владения - ?

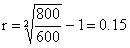
Пример:

Государственная краткосрочная облигация, N=100, была куплена за 85 у.е. и продана через 90 дней за 92 у.е

r за период владения - ?

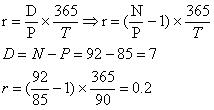
Пример: (эту задачу можно решать методом последовательных приближений или формулой для приблизительного расчета. Как вариант: можно тупо списать у Саши)

Инвестор приобретает облигации N=1000 за 930 у.е., через 2 года продает за 950. За время владения получал 200 у.е. в год.

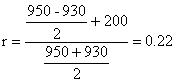
Реализованный процент

Теперь предположим, инвестор считает, что этот уровень доходности приемлем. Он оставляет облигацию у себя до погашения. Теперь его задача: не только посчитать купонные платежи, но и реинвестировать полученный доход для обеспечения уровня доходности.

Пример:

Облигация N=1000, погашение через 5 лет. Стоимость купона – 15%, проценты выплачиваются 1 раз в год.

Инвестор приобретает облигацию за 800 у.е., он рассчитывает, что сможет реинвестировать доходы под 20% годовых. Какую сумму будет иметь инвестор после погашения облигации?

1 шаг: определим доходы: ежегодные процентные платежи и доходы без реинвестирования

1й год – 150

2й год – 150

3й год – 150

4й год – 150

5й год – 1150

FV₁=150*(1+0.2)⁴=311

FV₂=150*(1+0.2)³=259

FV₃=216

FV₄=180

966 (начисленные проценты) + 150 (последний купонный доход) + 1000 = 2116

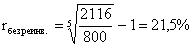
r_{без реинв.} = капитализируемая полностью наращенная ставка доходности или реализованный процент.

P = PV = 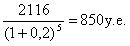- искомая цена облигации (курсовая), расчетная курсовая цена облигации.