Цели перестрахования, виды перестраховочных договоров, терминология. Математическая модель пропорционального перестрахования, эффект пропорционального перестрахования.
(!!!) здесь везде 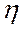 в степени *(звездочка)
в степени *(звездочка)
Модели перестрахования.
Главная цель - уменьшить риски страховой компании, передав часть рисков другим страховым компаниям. Делимся рисками -делимся доходами. Дилемма страховой компании - жадность и страх.
Страх при этом нормативров., нельзя взять больше, чем позволено. Нормативы меняются, размер риска связан с капиталом компании.
1. Пропорциональное страхование.
Z - размер риска, случайная величина страховой выплаты. Z=∑ 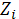
α - остается у цедента αZ (1-α)Z
(1-α) -переход к цессионарию
EZ- средний размер возмещения, ожидаемый по портфелю.
α(1+η)EZ - премия страховщика
(1-α)(1+ 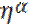 )EZ - премия перестраховщика
)EZ - премия перестраховщика
у - доход цедента
y=[η- 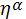 +(1+
+(1+ 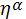 )α] EZ (*)
)α] EZ (*)
(1+η)EZ - (1-α)(1+ 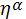 )EZ - остается на долю страховщика
)EZ - остается на долю страховщика
P(αZ > y) - вероятность разорения
 P(αZ > y) min(α)
P(αZ > y) min(α)
Подставим у(*) и разделим на α
 Р(Z > [
Р(Z > [ 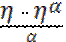 +(1+
+(1+ 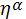 ) ]EZ) min(α)
) ]EZ) min(α)
Рассмотрим три случая:
1) η > 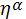 ( надбавка страховщика больше, чем перестраховщика)
( надбавка страховщика больше, чем перестраховщика)
если у=0, то страхователь получает безрисковый доход, что не бывает.
Своя доля завышена, на это никто не идет.
2) η = 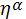
от α ничего не зависит. риск прежний, только теряются доходы.
 3) η <
3) η < 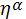 , α max
, α max
В рамках данной конструкции перестрахование не имеет смысла, но он есть:
η= 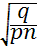 при условии:
при условии:
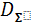 = ∑
= ∑ 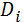 = nD - эта формула работает, когда cov=0
= nD - эта формула работает, когда cov=0
Допустим, имеется несколько регионов, в которых страховщики страхуют регионы от потери урожая. От страхования страдают все регионы, а не только один. В итоге риск делится поровну между всеми регионами ( 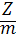 ),тогда
),тогда
η= 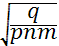
Эта схема позволяет понять, что за счет пропорционального перестрахования приобретается диверсификация, отсюда идет снижение рисковой надбавки или вероятности разорения.
24. Математическая модель непропорционального (эксцедентного) перестрахования. Общая схема. Численный пример.
(!!!) здесь везде 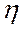 в степени *(звездочка)
в степени *(звездочка)
Непропорциональное страхование – илиСтрахование эксцедента убытка (stop-loss, передается то, что выше опред.суммы, котор.зависит от r). Перестрахование редко вступает в действие, но в этих случаях не несёт рисков – распределение убытка несимметрично.
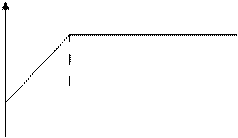
У нас есть риск Zi ,и он делится след. образом:

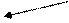 Z
Z
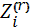 = min (
= min ( 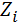 ,r)
,r) 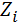 -
- 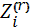 = max (0,
= max (0, 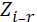 )
)
(Цедент) (Цессионарий)
Для перестраховщика эта ситуация ведения бизнеса - аналог франшизы.
 |
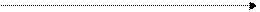 r
r 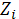
Z=∑ 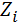
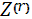 =∑
=∑ 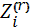
Для простоты все 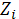 одинаковые:
одинаковые:
∑ 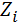 = µ, у перестраховщика только больше дисперсия.
= µ, у перестраховщика только больше дисперсия.
Доход страховщика без перестрахования : у=(1+η)EZ = (1+η) Nµ
Если он передает часть рисков в перестрахование, то:
у= N(1+ 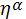 )(E
)(E 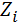 - E
- E 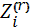 )
)
y - доход цедента =N(η- 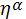 )µ + N(1+
)µ + N(1+ 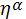 ) E
) E 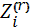
Как и раньше- задача минимизировать вероятность разорения.
P( 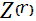 > y) = P (
> y) = P ( 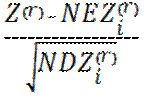 >
> 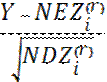 )
)
=
= 1 - Ф ( 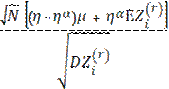 )
)
это C(r)
Т.к. Ф монотонно возрастает, то эта вероятность минимальна, когда Ф максимальна.
Но Ф à max, если C à max, C - функция от переменной r, которая нбх опред, из критерия:C(r) à max.
Пример
Пусть страховая компания имеет 10 000 договоров на 1 год.
Все договора одинаковые, имеем следующее распределение:
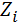 | 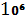 | 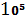 | |
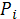 | 5 * 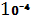 | 2* 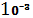 | 1-25* 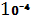 |
E 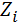 =5 *
=5 * 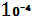 *
* 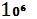 + 2*
+ 2* 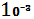 *
* 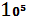 = 700
= 700
D 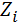 =5,2 *
=5,2 * 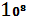
Пусть 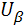 =
= 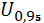 = 1,645
= 1,645
На 1 год: 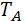 = E
= E 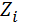 +
+ 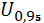 *
* 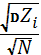 = 1075
= 1075
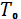
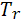
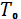 =700
=700
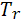 =375
=375
η= 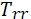 =
= 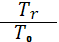 = 0,536
= 0,536
надбавка норм., тк большое N
Т.о.
y=(1+η) µN = (1+0,536) * 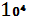 * 700 =10752000 ye
* 700 =10752000 ye
2) Пусть r = 105, т.е цессонарий возмещает более ???
также надо установить 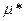 , у которой другое распред. риска
, у которой другое распред. риска
Пусть 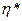 =0,6,
=0,6, 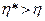 , т.к его диспресия больше
, т.к его диспресия больше
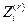 | 105 | |
| pi | 25*10-4=0.0025 | 1-25*10-4=0.9975 |
3) 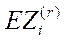 =250
=250
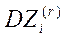 =25*106
=25*106
- почти бернул. распред.
До перестрахования доход цедента y=NT=1075*104
доход цессионария для 1-го договора 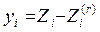
Распред. Ущерба для цессионария – риск за чертой r
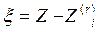 | 900 000 | |
| pi | 5*10-4 | 1-5*10-4 |
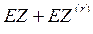 =9*105*5*10-4=т0 – нетто-ставка перестраховщика для цедента
=9*105*5*10-4=т0 – нетто-ставка перестраховщика для цедента
доход цессионария
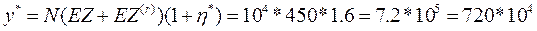
у цедента остается y’=355*104
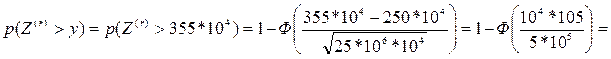 1-Ф(2,1)=0,018
1-Ф(2,1)=0,018
или вероятность разорения 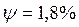
(риск разорения без цессии составляет5%, исходя из β=0,95)
Исследуем, как влияет лимит ответственности на параметры страховщика(риск его разорения, доход), если величина удержания произвольна
Можно ли найти оптимальное удержание?
Пусть r=r’/105, изменили ед. измерения для удобства
r=1 => Z(r)=105 ; r=10 => Z(r)=106
Таблица распределения, будем считать, что 1<r<10, те между 105 и 106
для цедента решьине была 1, qp-вер-ть)
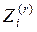 | r | ||
| pi | 5*10-4 | 20*10-4 | 1-25*10-4 |
Необходимо найти доход и риски для страховщика
Кол-во договоров 10 000, N=104
индивид 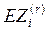 =5*10-4(r+4) => для N,
=5*10-4(r+4) => для N,  =5*(r+4)
=5*(r+4)
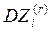 =5*(r2+4)*10-4 =>
=5*(r2+4)*10-4 => 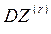 =5*(r+4)
=5*(r+4)
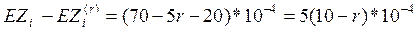 - среднее, то что получает перестраховщик.
- среднее, то что получает перестраховщик.
но у него еще есть накрутка – 1,6*5*10-4*(10-r)=8(10-r)* 10-4 – в расчете на одного человека, 1,6 – риск надбавки для перестраховщика
Т.к валюта поменялась, то 1075*10-1 =>107.5
y(r) =107.5-8(10-r) =27.5+8r
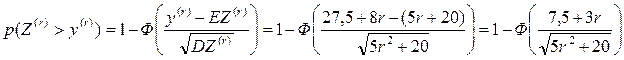 нам надо найти такое r, чтобы максимизировать функцию Ф, тем самым минимизировать разорение
нам надо найти такое r, чтобы максимизировать функцию Ф, тем самым минимизировать разорение
max rk=1.6 à160 000
h(r)à max(r)
hmax=2.15 à 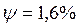
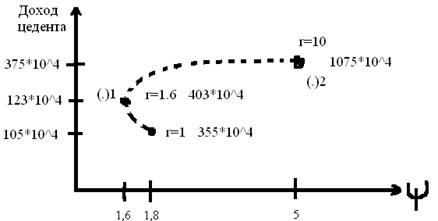
ниже r=1.6 – нет смысла рассматривать
выше - эффективное множество Парето-Эджуорта
в (.)1 – минимальные риски
в (.)2 – макс. доход
Вся задача рассматривается с позиции цедента.
