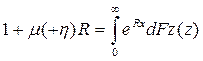Простейший (пуассоновский) процесс, его свойства, следствия из них. Сложнопуассоновский (составной пуассоновский) процесс, его вероятностные характеристики. Вывод формулы математического ожидания.

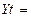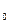у + ct - ,

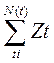где Yt – дискретная переменная – стартовый капитал страховщика, с – страховая премия, т.е. скорость, с кот в ст.комп. поступают средства, t – время,

N(t) – случайная величина, кол-во исков

N= 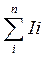, сумма индикаторов событий, EN = np = ν

N(t) – представляет собой пуассоновский процесс, его значениями явл. кол-во предъявл.исков.

P(N(t) = x) = [(λt)^x/x!]*e 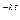- модель потока событий.

N(t)

T

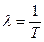- среднее время между 2 скачками, чем меньше T, тем интенсивней поток

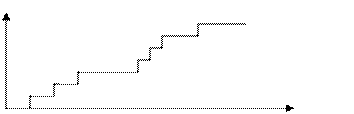
T - время между событиями, событие значит предъявление иска и возмещение компанией опред. ущерба – каждая ступень имеет высоту Zt,

EZt = 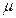- средняя величина ступеньки

Если ущерб каждый раз разный, ступеньки имеют разные высоты, то имеет место составной пуасон.процесс. (верхний рисунок)

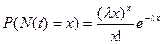
x=0,1….

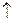генерирует поток событий

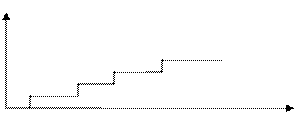
t

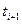
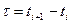
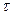- время между событиями. При t=1 модель становится однопериодной. Так же потоки являются аппаратами массового обслуживания.

Простейший пуассоновский процесс (нижний рисунок) – процесс с независимыми приращениями, обладает свойствами:

1) стационарность, т.е. вероятность появления х событий на интервале (t; t+ 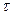) зависит от 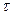-ширины интервала и от х, но не от t. Пара (х; 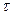) определяет интенсивность событий.

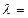постоянна, потому поток стационарен

P ( x(t;t+τ)=n ) = Pn(τ)

2) отсутствие последействия – предыстория не влияет на вероятности появления событий в будущем. Только начальное состояние влияет на будущее, прошлое не имеет значения, его нет.

x(t(i);t(i+1)) и x(t(i-1),t(i)) независимы

3) ординарность, т.е. вероятность появления в некотором «малом» интервале времени более чем одного события почти равна 0. Эта вероятность на порядок меньше, чем вероятность вообще ни одного события или одного события.

P ( N(t;t+∆t)≥2 ) = 0(∆t)

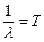- среднее время между событиями, малость означает , что 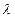T <<1

Следствием из этих св-в является то, что интервалы времени между событиями распределены экспоненциально, 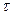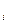= t(i+1)-t(i) распред экспоненциально

Проверка св-ва 3

1)

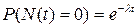
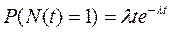
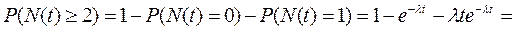
Разложим е в ряд Тейлора и будем считать, что 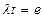, т.е 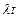-величина маленькая.

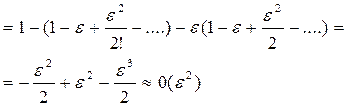
А если 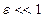, то 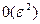является величиной второго порядка малости.

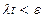означает, что интервал 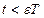, где T = 1/λ

Проверим следствие.

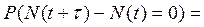
Т.к 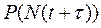от t не зависит, то можно положить, что t=0

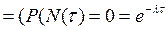
Это означает, что ф-я распределения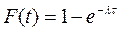

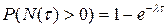, т.е τ – интервалы врем.между событиями - распред.экспоненциально.

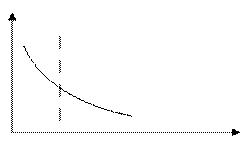
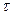
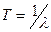
На рис. - кривая 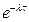и мат.ож. Т

Вероятностные характеристики сложного пуассон. процесса

Составной Пуассоновский процесс N(t)

Zi =Ii Si Ri

n – число договоров, EIi = p , сл-но, EN = np

Обозначения

ERi =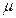

DRi =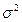

EN = ν

DN =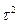

Вывод формулы мат.ож.

Z= 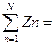, N=1,2,3……, Zn – независимые друг от друга, одинаково распред.

Т.к. Zi = Ii*Si*Ri, Ii переводится в N => Zi = Si*Ri, Si=1, => Zi = Ri => Z =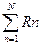

Если Rn = R, то Z = R*N (неправильно с точки зрения распределений, но в этом случае это вып)

Надо найти EZ, DZ

Если бы Z=NR, то как неоднородный портфель (???)

EZ= 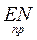* 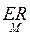= n*p*μ = ν*μ

Если Z≠NR, действуя строго, получим EZ= 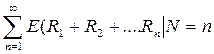) * p(N=n)

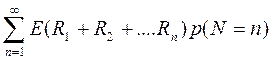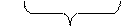= = =E R 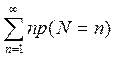= ER EN

EN

DZ = DN*DR+(E²N)*DR+(E²R)*DN = τ²σ²+ν²σ²+μ²τ² = νσ²+μ²τ²

10. Модель коллективного риска (стохастическое уравнение динамики страховых резервов). Вероятность разорения страховой компании как функция начального капитала и рисковой надбавки. Случай экспоненциального распределения индивидуальных исков. Общий случай (неравенство Лундберга-Крамера).

Модель коллективного риска имеют следующие допущения:

1) Процесс поступления рисков растянут во времени. У нее есть динамика, при этом не рассматривается вероятность индивидуальных рисков (нет n и p и количества договоров).

2) Размеры выплат друг от друга не зависят

3) В страховую компанию поступает непрерывно во времени приток договоров с некоторой интенсивностью.

Рассматривается динамика резервов. Ставится задача: как параметры договоров (величина страховой премии, зависящей от страхового тарифа) и капитала (стартовая величина) влияют на вероятность разорения компании (то есть момент, когда резервы станут <0)

Yt – дискретная переменная – стартовый капитал страховщика

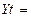у 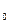+ ct -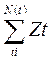

с – страховая премия, т.е. скорость, с кот в ст.комп. поступают средства, t – время

N(t) – случайная величина, кол-во исков

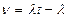интенсивность, скорость

E(ct)=EZ= 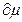, тогда C= 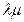, С - страховая премия, тариф.

реально учит риск.надбавка C= 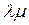*(1+ 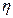), из Т = Т0 + Тr

Тогда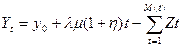

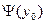вероятность разорения при стартовом капитале Y0

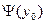=p(Yt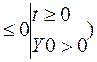

Если Y0<0 , то 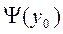=1

Величину 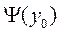можно получить, решая интегрально дифференциальное уравнение.

Если Z распределяется по экспоненциальному закону F(Z) = P(Zt 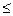Z) = 1- e 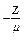(что наиболее приближено к реальности), то имеется решение:

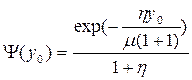
Если y 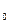=0 , то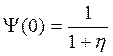

0<η<1, и чем больше риск.надбавка, тем меньше вер-ть разорения.

Небобх сравнивать Y0 с 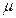-средние суммы, на которые мы страхуем, т.е рассм. (Y0/ 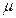) - кратность

В общем случае – если Z распред произвольно - имеет место неравенство Крамера-Лундберга

,

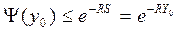где R -положительный корень интегрального уравнения