Цель страхования. Простейшая математическая модель страхования (с позиции страхователя), критерии справедливости и выгодности страхования для страхователя.
Страховое покрытие.
Страховое покрытие (покрытие страховой стоимости имущества или иного риска) – это уровень принятого в договоре страхования или в законе объема страховой ответственности страховщика денежной оценки по отношению к их действительной стоимости.
Разница между страховой стоимостью и страховой суммой называется декувер.
Выделяются 3 вида страхового покрытия:
1. Система пропорционального страхового покрытия. Возмещается величина пропорциональная страховой стоимости или ущербу.
2. Система покрытия первого риска. Возмещается ущерб в размере страховой суммы , установленной законом или договором страхователя, которая меньше страховой стоимости.
3. Система предельного страхового покрытия. Используется часто при страховании рисков п/п деятельности. Этот вид предусматривает возмещение ущерба, определяемого в виде разницы между установленной договором реально достижимой величины дохода и фактической меньшей их величиной.
Страхование с франшизой.
Франшиза – предусмотренное условиями страхования освобождение страховщика от возмещения ущерба не превышающих определенны размер, % величины, которая не возмещается, остается на удержании страхователя.
Величина, которая не возмещается, остается на удержании страхователя.
Франшиза преследует цели поддержания устойчивости страховой компании за счет уменьшения больших объемов выплат малых сумм. Этим достигается эффект либо снижения страховых тарифов, либо повышения (при тех же тарифах) уровня ответственности.
Различают условную (невычитаемую) и безусловную (вычитаемую) франшизу, которая устанавливается в виде % или как абсолютная величина.
| |
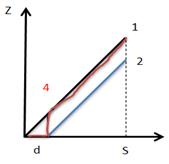
S – страховая стоимость.
Z – ущерб.
1 - ущерб
Безусл фр – схема 2
Условная фр – 3 (до d страховщик не платит ничего, после d – оплачивает полностью все)
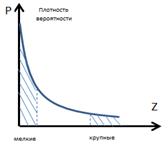
Размер франшизы зависит от категории страхователей¸ вида застрахованного имущества, перечня страховых рисков, включенных в договор страхования и т.д.
Бывает и так:

|
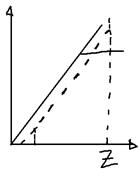
Способы деления рисков.
Выделяют два способа деления риска:
1. Сострахование - производится по отдельным крупным договорам путем создания страховщиками страхового пула по отдельному, конкретному договору.
2. Перестрахование – называется страхование одним страховщиком (перестрахователь, цедент) на определенных договором условиях риска исполнения всех или части своих обязательств перед страхователем у другого страховщика (перестраховщик, цессионарий).

|
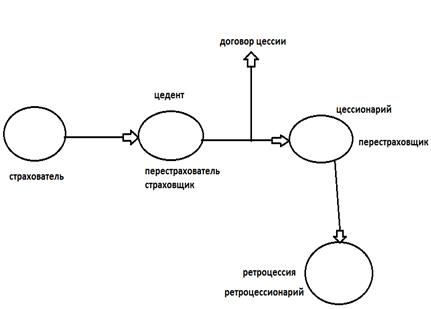
Объем ответственности, принятой на себя страхователем называется эксцедентом.
Эти виды стр.деят-ти связаны с тем, что страховщик чувствует невозможность самостоятельно гаранитировать необх-мый уровень стр.защиты либо не имеет право по закону брать на себя опр-й уровень ответственности.
Существует две формы перестрахования:
1. Договорная
2. Факультативная (в отличие от договорной осуществляется без заранее установленных соглашений по передаче обязательств)
Выделяются следующие 4 типа договоров страхования:
1. Квотное пропорциональное – страховщик передает перестрахование, согласно заранее установленному проценту, часть всех принятых на страхование рисков по опр-м видам страхования (прибыль и риски делятся пропорционально)
2. Эксцедентное пропорциональное – устанавливается конкретная сумма собств-й ответст-ти страховщика по каждому передаваемому риску
3. Непропорциональное стр-ние эксцедента убытка – предполагается что страховщик передает ответст-ть в том случае, если объем выплат превышает некот-й лимит ответст-ти.
4. Непропорциональное стр-е эксцедента убыточности – перестраховщик вступает в дело, когда убыточность стр-й суммы превышает заране установленный предел.
Убыточность стр-й суммы – средняя величина выплат в рублях с единицы измерения совокупной стр-й суммы по виду страхования и в масштабах территории за опр-й период.
С позиции математики для перестраховщика (цессионария) цедент играет роль франшизы.
Определение тарифа в случае неоднородного страхового портфеля. Реальный страховой портфель. Определение тарифа и исследование зависимости величины относительной рисковой надбавки от характеристик портфеля.
Отличие в том, что все Si разные.
Мы будем их усреднять.
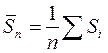 ,
, 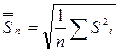
EZ = 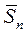 np , DZ =
np , DZ = 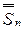 ²npq
²npq
Q = 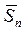 nT
nT
nT 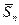 =
= 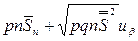
T = 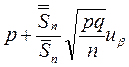
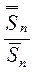 =
= 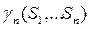 - коэф.неоднородности (учитывает неоднородность страхового портфеля)
- коэф.неоднородности (учитывает неоднородность страхового портфеля)
1< 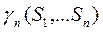 <√n
<√n
=1 – если все Si равны
=√n – если все Si=0 кроме одного
В рекомендациях 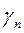 =1,2
=1,2
Страхования компания по идее должна считать величину γ.
(А вообще считается, что все Si не должны сильно отличаться друг от друга.)
Вывод формулы мат.ож.
Z= 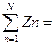 , N=1,2,3……, Zn – независимые друг от друга, одинаково распред.
, N=1,2,3……, Zn – независимые друг от друга, одинаково распред.
Т.к. Zi = Ii*Si*Ri, Ii переводится в N => Zi = Si*Ri, Si=1, => Zi = Ri => Z = 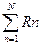
Если Rn = R, то Z = R*N (неправильно с точки зрения распределений, но в этом случае это вып)
Надо найти EZ, DZ
Если бы Z=NR, то как неоднородный портфель (???)
EZ= 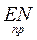 *
* 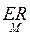 = n*p*μ = ν*μ
= n*p*μ = ν*μ
Если Z≠NR, действуя строго, получим EZ= 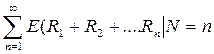 ) * p(N=n)
) * p(N=n)
= 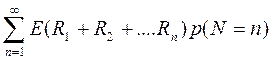 = =E
= =E 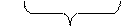 R
R 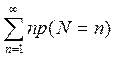 = ER EN
= ER EN

EN
DZ = DN*DR+(E²N)*DR+(E²R)*DN = τ²σ²+ν²σ²+μ²τ² = νσ²+μ²τ²
10. Модель коллективного риска (стохастическое уравнение динамики страховых резервов). Вероятность разорения страховой компании как функция начального капитала и рисковой надбавки. Случай экспоненциального распределения индивидуальных исков. Общий случай (неравенство Лундберга-Крамера).
Модель коллективного риска имеют следующие допущения:
1) Процесс поступления рисков растянут во времени. У нее есть динамика, при этом не рассматривается вероятность индивидуальных рисков (нет n и p и количества договоров).
2) Размеры выплат друг от друга не зависят
3) В страховую компанию поступает непрерывно во времени приток договоров с некоторой интенсивностью.
Рассматривается динамика резервов. Ставится задача: как параметры договоров (величина страховой премии, зависящей от страхового тарифа) и капитала (стартовая величина) влияют на вероятность разорения компании (то есть момент, когда резервы станут <0)
Yt – дискретная переменная – стартовый капитал страховщика
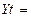 у
у 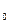 + ct -
+ ct - 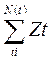
с – страховая премия, т.е. скорость, с кот в ст.комп. поступают средства, t – время
N(t) – случайная величина, кол-во исков
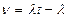 интенсивность, скорость
интенсивность, скорость
E(ct)=EZ= 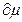 , тогда C=
, тогда C= 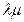 , С - страховая премия, тариф.
, С - страховая премия, тариф.
реально учит риск.надбавка C= 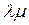 *(1+
*(1+ 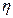 ), из Т = Т0 + Тr
), из Т = Т0 + Тr
Тогда 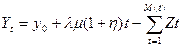
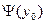 вероятность разорения при стартовом капитале Y0
вероятность разорения при стартовом капитале Y0
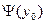 =p(Yt
=p(Yt 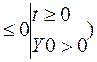
Если Y0<0 , то 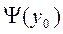 =1
=1
Величину 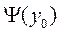 можно получить, решая интегрально дифференциальное уравнение.
можно получить, решая интегрально дифференциальное уравнение.
Если Z распределяется по экспоненциальному закону F(Z) = P(Zt 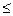 Z) = 1- e
Z) = 1- e 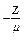 (что наиболее приближено к реальности), то имеется решение:
(что наиболее приближено к реальности), то имеется решение:
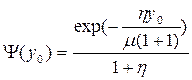
Если y 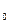 =0 , то
=0 , то 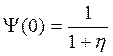
0<η<1, и чем больше риск.надбавка, тем меньше вер-ть разорения.
Небобх сравнивать Y0 с 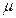 -средние суммы, на которые мы страхуем, т.е рассм. (Y0/
-средние суммы, на которые мы страхуем, т.е рассм. (Y0/ 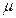 ) - кратность
) - кратность
В общем случае – если Z распред произвольно - имеет место неравенство Крамера-Лундберга
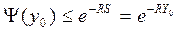 ,
,
где R -положительный корень интегрального уравнения
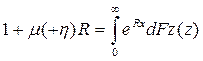
Основные вероятностные характеристики, используемые в страховании жизни (безусловные и условные вероятности дожития, интенсивность смертности, средняя продолжительность жизни при рождении, средняя остаточная продолжительность жизни). Таблицы выживаемости (смертности). Отличие средних при использовании непрерывной и дискретной моделей.




 Введём случайную величину X – продолжительность жизни при рождаемости. Тогда P(X>x)=s(x), F(x)=P(X≤x)=1-s(x)
Введём случайную величину X – продолжительность жизни при рождаемости. Тогда P(X>x)=s(x), F(x)=P(X≤x)=1-s(x)
s(x)
P( 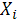 >x)
>x)
x
Введём случайную величину L(x) – количество людей доживших до возраста x, причём lx – конкретная фактическая известная величина, поэтому значение приближённое:
l(x)=EL(x) ~~  , т.е. l(x)=
, т.е. l(x)=
I-индикатор события дожития A=( 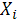 >x) (дожил-1, не дожил-0), поэтому её мат.ож. равно вер-ти А.
>x) (дожил-1, не дожил-0), поэтому её мат.ож. равно вер-ти А.
Обознач. 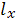 -если величина дискретная, l(x) - если возраст считать непрерывной величиной
-если величина дискретная, l(x) - если возраст считать непрерывной величиной
На практике используется не функция, а таблица (дискретная вел-на кол-ва людей):
| x | 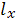 | 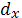 | 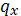 | 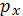 |
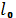 | ||||
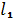 | ||||
| … | ||||
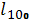 |
Начальная графа – стартовый размер когорты 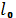 -корень таблицы, который показывает её точность (1000, 10000, …), и чем больше, тем точнее.
-корень таблицы, который показывает её точность (1000, 10000, …), и чем больше, тем точнее.
Количество умерших за год в когорте: dx= 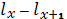
Вероятность того что человек дожил до возраста x, но вероятность мереть в следующем году: 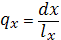
Это вероятность условная - при условии, что человек дожил
Вероятность прожить ещё год: 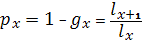
Количество смертей (умерших), человек дожил до возраста x, но умер в ближайшие n лет: ndx= 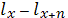
Соответственно условные вероятности
n 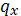 =ndx/
=ndx/ 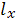 ; n
; n 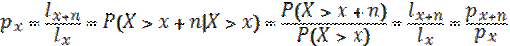
Найдём вероятность умереть на интервале [x, x+t]:
P(x<X≤x+t|X>x)= 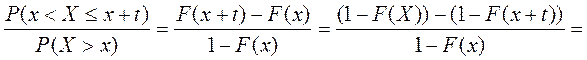
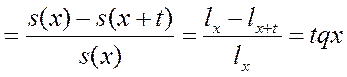
Пусть t малая величина, тогда:
t 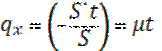
-мгновенная смерть/интенсивность смертей
S=1-F
S`=-fÞm(x)= 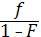 – показывает риск умереть в возрасте х
– показывает риск умереть в возрасте х
В теории вероятности такая функция называется функцией риска
Среднее время жизни.
1) Среднее время жизни при рождении. 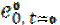
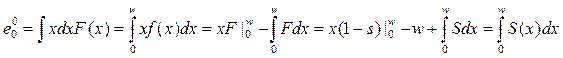
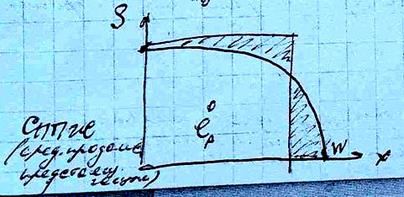
2) Остаточная продолжит.жизни – случ.величина, её мат.ож – средняя остаточная продолжит.жизни
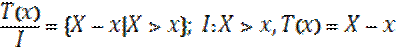
Найдем распределение 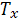 :
:
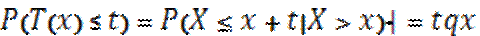
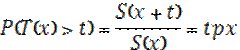
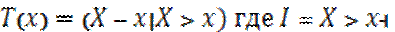
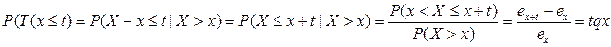
вероятность умереть в интервале(x;x+t)
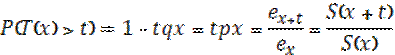
T(x)=X-x (?)
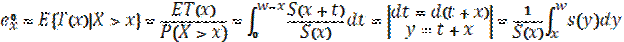
t – сколько осталось прожить
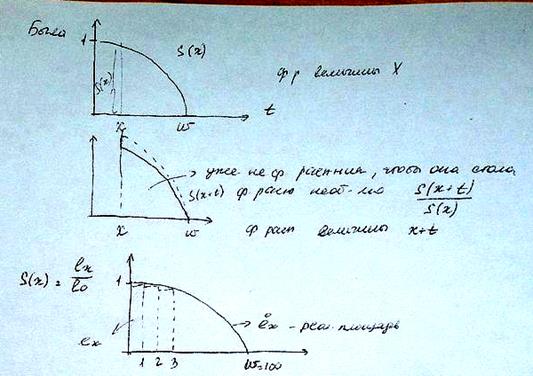
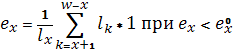
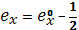 - приближенно
- приближенно
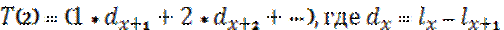
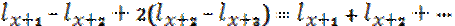
Рассмотрим вероятность того, что человек, доживший до возрастра x проживет еще m лет, но умрет в последующий n лет:

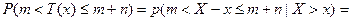
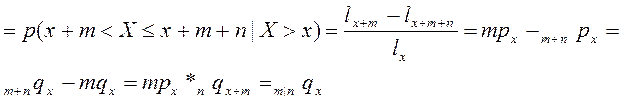
- отложенная смерность
Пожизненное страхование.
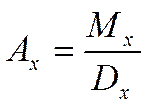
По этим контрактам страховое возмещение выплачивается в конце года.
Логическая схема:
Единовременные контракты делятся на:
- дожития (срочный) 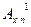
- на случай смерти: - срочный 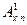
- бессрочный 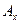
дожития + срочный на случай смерти => смешанный 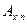
также выделяют отсроченный на m – любой из них м.б отсрочен
Можно записать выражение одного через другие:
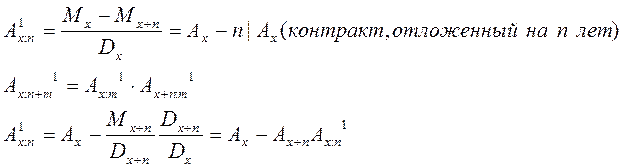
Страховые аннуитеты
Аннуитетом называются регулярные потоки платежей. Они бывают:
- страховые - связанные с вероятностью
- финансовые – рентные платежи,
также
- аннуитет постнумерандо — выплата осуществляется в конце первого периода,
- аннуитет пренумерандо — выплата осуществляется в начале первого периода.
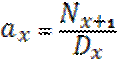
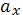 - стоимость пенсии с фиксированным размером платежей
- стоимость пенсии с фиксированным размером платежей
Аннуитет с пренумерандо- авансовая рента
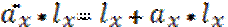
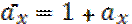
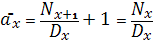
Как видно из этих формул, аннуитет представл собой сумму срочных контрактов, и состоит из суммы А
Аналогично строятся аннуитеты для срочных контрактов.
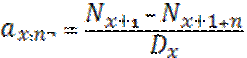
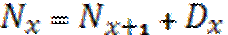
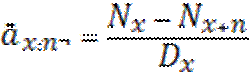
- таким соответствует отложенный аннуитет
Отложенный аннуитет – между моментом внесения денег и моментом начала получения денег проходит m лет
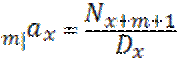
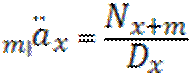
Срочные отложенные на m лет аннуитеты
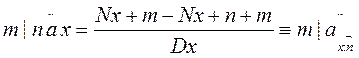
Страховые аннуитеты:
1. Срочные:
-отложенные m|n 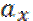 m|n
m|n 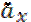
-немедленные 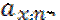
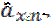
2. Пожизненные:
-отложенные m| 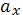 m|n
m|n 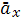
- немедленные 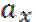
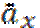
Пожизненное страхование.
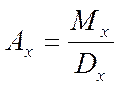
По этим контрактам страховое возмещение выплачивается в конце года.
Связи между аннуитетами
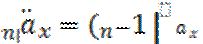
- аннуитет постнумерандо – это отложенный на 1 год аннуитет преднумерандо.
Страховые взносы
Расчет страховых премий(взносов) в случае пожизненной или ограниченной рассрочки платежей
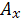 - пожизн на случай смерти (бессрочные контракт)
- пожизн на случай смерти (бессрочные контракт)
Сколько страхователь должен ежегодно вносить, если он получает 1 руб. в случае смерти для пожизненного контракта на случай смерти. Рассчитаем страховой взнос
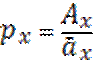
Если контракт срочный
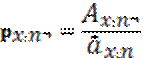
Пусть мы хотим платить не все время, а только некоторый период t<n, тогда
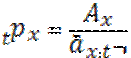
Для пенсионных схем характерна следующая схема
m|nP= 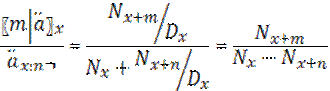
n – период, в течении которого платятся страховые взносы.
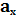 – та рента, которую получает страхователь, отложенную на m лет
– та рента, которую получает страхователь, отложенную на m лет
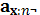 - период, в течении которого производится рассрочка
- период, в течении которого производится рассрочка
Если платежи проводятся несколько раз в течении года, то взносы рассчитываются путем интерполяции
Групповые контракты – илиРеверсивные аннуитеты
Пусть
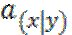 – стоимость единичной ренты для у в случае смерти (можно
– стоимость единичной ренты для у в случае смерти (можно 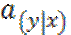
наоборот)
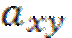 – стоимость ренты, если живы х и у
– стоимость ренты, если живы х и у
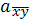 – если жив хотя бы один.
– если жив хотя бы один.
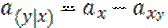
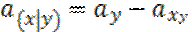
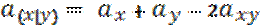
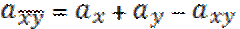
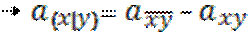
Обязательное (ОМС) и добровольное (ДМС) медицинское страхование, схема организации. Особенности установления страховой суммы и страхового тарифа в ДМС, специфика коммутационных функций, используемых в медицинском страховании. Медицинское страхование лиц, выезжающих за рубеж.
Медицинское страхование — форма социальной защиты интересов населения в охране здоровья, выражающаяся в гарантии оплаты медицинской помощи при возникновении страхового случая за счёт накопленных страховщиком средств.
Медицинское страхование позволяет гарантировать гражданину бесплатное предоставление определённого объёма медицинских услуг при возникновении страхового случая (нарушении здоровья) при наличии договора со страховой медицинской организацией. Последняя несёт затраты по оплате случая оказания медицинской помощи (риска) с момента уплаты гражданином первого взноса в соответствующий фонд.
1. Обязательное медицинское страхование — вид обязательного социального страхования, представляющий собой систему создаваемых государством правовых, экономических и организационных мер, направленных на обеспечение при наступлении страхового случая гарантий бесплатного оказания застрахованному лицу медицинской помощи за счет средств обязательного медицинского страхования в пределах территориальной программы обязательного медицинского страхования и в случаях, установленных Федеральным законом, в пределах базовой программы обязательного медицинского страхования.
Права страхователя
· участие во всех видах медицинского страхования;
· свободный выбор страховой медицинской организации;
· контроль выполнения условий договора ОМС.
Финансовые потоки, если надо
|
| ||||
|




|


 взнос за
взнос за
 неработающих
неработающих
|
|



|
|
|
ДМС
ОМС
ДМС
2. Добровольное медицинское страхование является дополнительной программой к установленному объёму медицинской помощи, что действует для лиц, указанных страхователями в качестве выгодополучателей. ДМС осуществляется за счёт средств определённого бюджета, личных взносов граждан, взносов работодателя.
Следует отметить, что ДМС страхует не здоровье, но затраты на лечение; последние возмещаются застрахованному обыкновенно или по этапу медицинского вмешательства (фармакология, диагностика, стационар), или по видам оказанной медицинской помощи (стоматология, гинекология, косметология, случай смерти), или по долям расходов на оплату оказанной медицинской помощи (полное возмещение, процентное возмещение, возмещение в пределах определённой суммы).
В нашей стране страховые тарифы по ДМС в настоящее время превышают 70-
80% при рисковых формах страхования. Такие тарифы при установлении цивилизованных рыночных взаимоотношений на страховом рынке не будут коонкурентноспособны. Размер платы за страховую услугу, в качестве которой выступает страховой взнос, должен зависеть от реальной стоимости риска, определение которой на сегодняшний день осложнено либо полным отсутствием статистических данных, либо их недостоверностью.
ДМС можно представить в следующем виде:
Ддмс = Пр + И + др., где Ддмс - доходы ДМС,
Пр - сумма страховых премий, поступающих организациям ДМС,
И - доходы от инвестирования временно свободных денежных средств в ЦБ,
Др. - прочие источники финансирования, не запрещенные действующим законодательством.
Таким образом, доходная часть организаций, занимающихся ДМС складывается из следующих поступлений: страховых премий по договорам страхования, доходов от инвестирования временно свободных денежных средств в ценные бумаги и иных поступлений.
Прослеживается тенденция получения организациями, занимающимися ДМС, доходов от инвестирования средств (временно свободного остатка) в государственные ценные бумаги, банковские депозиты, ценные бумаги акционерных обществ, валютные ценности в соответствии с валютным регулированием, на условиях возвратности, прибыльности, ликвидности.
Порядок расчетов стоимости страхового полиса имеет следующие этапы:
1. Определение показателя вероятности наступления страховых событий по каждому виду медицинских услуг, включенных в страховое покрытие по данной программе страхования.
2. Определение основной части нетто-ставки (Тосн.) Для определения основной части нетто-ставки используются следующие формулы:
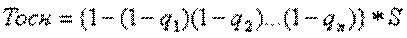 (7.16)
(7.16)
где q - вероятность появления хотя бы одного из рассматриваемых п событий, включенных в страховое покрытие по данной программе страхования;
S – размер базовой страховой суммы (100 руб.).
3. Определение рисковой надбавки (Триск.). Определяется по формулам, приведенным выше.
4. Определение нетто-ставки (Тн):
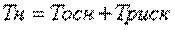 (7.17)
(7.17)
5. Определение максимальной суммы страхового покрытия (Sм)
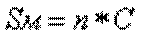
где n - максимальное количество обращений за медицинской помощью одним застрахованным в течение срока страхования;
С – стоимость одного обращения, руб.
6. Расчет коэффициента соотношения рисков (К с.р.). Его использование имеет смысл тогда, когда среднее число обращений за медицинской помощью застрахованных меньше, чем максимальное. Использование этого коэффициента позволяет снизить размер страхового тарифа.
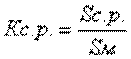 (7.18)
(7.18)
где S с.р. – среднее страховое покрытие;
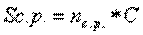 (7.19)
(7.19)
где 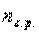 – среднее количество обращений за медицинской помощью одним застрахованным в течение срока страхования.
– среднее количество обращений за медицинской помощью одним застрахованным в течение срока страхования.
7. Определение нетто-стоимости страхового полиса по ДМС (Пн):
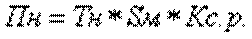 (7.20)
(7.20)
где Т н – нетто-ставка в %.
8. Определение брутто-стоимости полиса по ДМС (Пб):
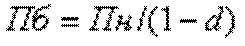 (7.21)
(7.21)
где d - доля нагрузки в составе брутто-ставке
3. Медицинское страхование выезжающих за рубеж (путешественников)
Данный вид страхования является добровольным видом страхования, однако наличие полиса страхования медицинских расходов выезжающих за рубеж (ВЗР) является обязательным требованием для получения визы в ряд стран (страны Шенгенского соглашения и др.)
Ведется обсуждение о введении данного вида страхования в число обязательных, при оформлении поездки через туристическую фирму.
Правилами страхования конкретной страховой компании определяется объем услуг, оплачиваемых полисом ВЗР, но, как правило, это:
· Медицинские услуги — лечение остро возникших заболеваний или травм
· Медико-транспортные услуги — доставка пациента до больницы, перевозка из одной больницы в другую, при необходимости — эвакуация пациента в страну постоянного проживания, с сопровождением.
· Репатриация останков
Модели перестрахования.
Главная цель - уменьшить риски страховой компании, передав часть рисков другим страховым компаниям. Делимся рисками -делимся доходами. Дилемма страховой компании - жадность и страх.
Страх при этом нормативров., нельзя взять больше, чем позволено. Нормативы меняются, размер риска связан с капиталом компании.
1. Пропорциональное страхование.
Z - размер риска, случайная величина страховой выплаты. Z=∑ 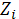
α - остается у цедента αZ (1-α)Z
(1-α) -переход к цессионарию
EZ- средний размер возмещения, ожидаемый по портфелю.
α(1+η)EZ - премия страховщика
(1-α)(1+ 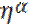 )EZ - премия перестраховщика
)EZ - премия перестраховщика
у - доход цедента
y=[η- 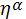 +(1+
+(1+ 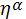 )α] EZ (*)
)α] EZ (*)
(1+η)EZ - (1-α)(1+ 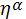 )EZ - остается на долю страховщика
)EZ - остается на долю страховщика
P(αZ > y) - вероятность разорения
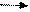 P(αZ > y) min(α)
P(αZ > y) min(α)
Подставим у(*) и разделим на α
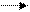 Р(Z > [
Р(Z > [ 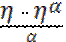 +(1+
+(1+ 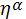 ) ]EZ) min(α)
) ]EZ) min(α)
Рассмотрим три случая:
1) η > 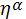 ( надбавка страховщика больше, чем перестраховщика)
( надбавка страховщика больше, чем перестраховщика)
если у=0, то страхователь получает безрисковый доход, что не бывает.
Своя доля завышена, на это никто не идет.
2) η = 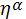
от α ничего не зависит. риск прежний, только теряются доходы.
 3) η <
3) η < 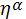 , α max
, α max
В рамках данной конструкции перестрахование не имеет смысла, но он есть:
η= 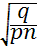 при условии:
при условии:
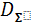 = ∑
= ∑ 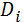 = nD - эта формула работает, когда cov=0
= nD - эта формула работает, когда cov=0
Допустим, имеется несколько регионов, в которых страховщики страхуют регионы от потери урожая. От страхования страдают все регионы, а не только один. В итоге риск делится поровну между всеми регионами ( 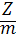 ),тогда
),тогда
η= 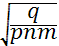
Эта схема позволяет понять, что за счет пропорционального перестрахования приобретается диверсификация, отсюда идет снижение рисковой надбавки или вероятности разорения.
24. Математическая модель непропорционального (эксцедентного) перестрахования. Общая схема. Численный пример.
(!!!) здесь везде 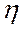 в степени *(звездочка)
в степени *(звездочка)
Непропорциональное страхование – илиСтрахование эксцедента убытка (stop-loss, передается то, что выше опред.суммы, котор.зависит от r). Перестрахование редко вступает в действие, но в этих случаях не несёт рисков – распределение убытка несимметрично.
У нас есть риск Zi ,и он делится след. образом:

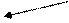 Z
Z
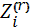 = min (
= min ( 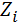 ,r)
,r) 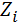 -
- 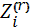 = max (0,
= max (0, 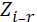 )
)
(Цедент) (Цессионарий)
Для перестраховщика эта ситуация ведения бизнеса - аналог франшизы.
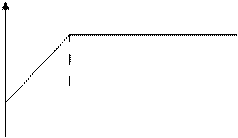 |
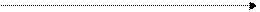 r
r 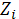
Z=∑ 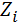
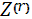 =∑
=∑ 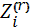
Для простоты все 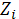 одинаковые:
одинаковые:
∑ 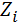 = µ, у перестраховщика только больше дисперсия.
= µ, у перестраховщика только больше дисперсия.
Доход страховщика без перестрахования : у=(1+η)EZ = (1+η) Nµ
Если он передает часть рисков в перестрахование, то:
у= N(1+ 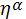 )(E
)(E 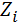 - E
- E 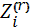 )
)
y - доход цедента =N(η- 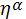 )µ + N(1+
)µ + N(1+ 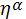 ) E
) E 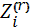
Как и раньше- задача минимизировать вероятность разорения.
P( 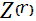 > y) = P (
> y) = P ( 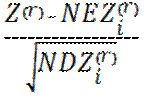 >
> 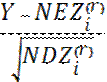 )
)
=
= 1 - Ф ( 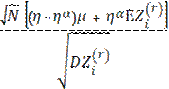 )
)
это C(r)
Т.к. Ф монотонно возрастает, то эта вероятность минимальна, когда Ф максимальна.
Но Ф à max, если C à max, C - функция от переменной r, которая нбх опред, из критерия:C(r) à max.
Пример
Пусть страховая компания имеет 10 000 договоров на 1 год.
Все договора одинаковые, имеем следующее распределение:
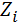 | 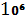 | 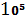 | |
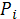 | 5 * 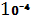 | 2* 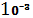 | 1-25* 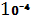 |
E 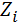 =5 *
=5 * 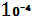 *
* 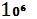 + 2*
+ 2* 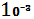 *
* 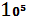 = 700
= 700
D 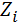 =5,2 *
=5,2 * 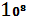
Пусть 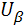 =
= 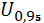 = 1,645
= 1,645
На 1 год: 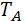 = E
= E 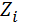 +
+ 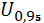 *
* 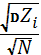 = 1075
= 1075
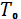
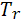
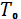 =700
=700
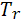 =375
=375
η= 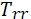 =
= 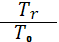 = 0,536
= 0,536
надбавка норм., тк большое N
Т.о.
y=(1+η) µN = (1+0,536) * 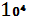 * 700 =10752000 ye
* 700 =10752000 ye
2) Пусть r = 105, т.е цессонарий возмещает более ???
также надо установить 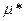 , у которой другое распред. риска
, у которой другое распред. риска
Пусть 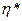 =0,6,
=0,6,
