Определение курсовой стоимости акции

С точки зрения теоретического подхода цена обыкновенной акции должна определяться дисконтированием всех доходов. Если инвестор планирует в будущем продать акцию, он может оценить ее стоимость по формуле:

.

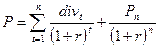где

Р - цена акции;

div₁ - дивиденд, который будет выплачен в периоде t;

r - ставка дисконтирования (доходность), которая соответствует уровню риска инвестирования в акции данного акционерного общества.

Другим упрощенным методом, определения курсовой стоимости акций, является модель постоянного роста дивидендов. Предполагается, что дивидендный доход растет от года к году, и что ценная бумага не будет продана. Скорость роста определяется ставкой g. Цена акции для модели постоянного роста дивидендов:

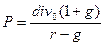(46)

где

P – курс акции

r – доходность равная риску инвестирования в акцию

g – темп прироста дивиденда

div₀ – фактический последний дивиденд, выплаченный на акцию

Из предыдущего выражения можно определить темп прироста будущих дивидендов

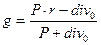
Темп прироста на основе прошлых данных (как выплачивался дивиденд в прошлом) определяется по формуле:

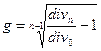
div₀ – начальный дивиденд

div_n – последний дивиденд

Модель постоянного роста дивидендов во многих случаях "не работает". Согласно модели постоянного роста дивидендов цена акции также должна расти тем же темпом роста, в то время как в действительности цена может изменяться и по другому. Бесконечный рост дивидендов и стоимости предприятия практически невозможен, так как для любого предприятия доходность инвестиций со временем уменьшается.

Стабильная дивидендная политика может оказывать влияние на рост цены акции. Однако опыт развитых рынков показывает, что дивидендная политика предприятия не так сильно влияет на цену акции, как темп роста прибыли предприятия.

Пример 25. Последний годовой дивиденд акции составил 16 руб. Предполагается, что дивидендные доходы и стоимость акции будут возрастать с годовым темпом 10%. Определить стоимость акции, если ставка дисконтирования выбрана 26%.

Решение: В соответствии с (46) прогнозируемая цена акции

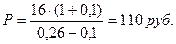
Если темп прироста дивиденда по акции будет различным на протяжении двух периодов времени, то ее курс можно определить по формуле:

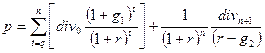
g₁ – темп прироста дивиденда за первый период, продолжительностью n лет,

g₂ - темп прироста дивиденда за последующие годы

div₀ – дивиденд за истекший год

При этом, если за первый период дивиденд не выплачивают, тогда формула сокращается до вида

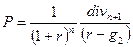
Пример 14

За истекший год был выплачен дивиденд в 200 руб. на акцию, темп прироста дивиденда равен 5%, ставка дисконтирования составляет 25%. Определить курсовую стоимость акции.

Решение.

Прогнозируемый на следующий год дивиденд равен: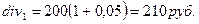

Акция должна стоить: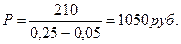

Форвардная ставка

Часто, в рамках вашей финансовой политики, бывает необходимо определить форвардную ставку для какого-то временного периода.

Пример 15

Ставка спот для шести месяцев равна 8% годовых, для четырех месяцев – 7,4%. Определить форвардную ставку для двух месяцев через четыре месяца.

Решение

Зависимость между форвардной и спотовой ставками на основе простого процента имеет вид:

,

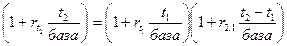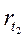- спот ставка для периода ,

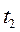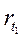- спот ставка для периода ,

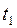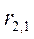- спот ставка для периода .

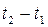Тогда, выразив искомую форвардную ставку 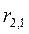получим:

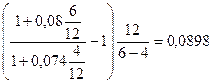или 8,98%

Если же при расчетах используется сложный процент, то форвардная ставка находится из соотношения:

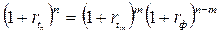
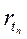- спот ставка для периода ,

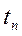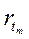- спот ставка для периода ,

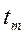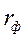- спот ставка для периода .

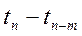Если известна цена облигации, ее номинал и купон, то можно рассчитать теоретическую ставку спот для какого-либо периода n. При этом ставки спот для оставшихся n-1 периодов должны быть известны:

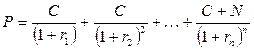
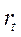- ставка спот для периода t; t = 1, 2, … , n