Р, вычисленное прямо и косвенно

Итак, мы вычислили независимо друг от друга все величины уравнения обмена для 14 лет - от 1896 до 1909 г. Но, как уже было установлено, эти шесть величин взаимно связаны уравнением обмена. Возникает вопрос: могут ли вычисленные таким образом величины хотя бы приблизительно осуществить уравнение обмена?

Один путь ответа на этот вопрос предложен проф. Kemmerer'ом, а именно он предлагает сравнить статистические данные для каждого отдельного фактора (скажем, для Р), вычисленные непосредственно, как указано выше, со значением этого фактора, вычисленным косвенно, при помощи других пяти величин уравнения обмена. Следующая таблица дает значения Р, полученные этими двумя способами.

Index numbers цен, вычисленные

Год	Непосред- ственно (Р)	(MV+M’V’)/Т

Соответствие между этими двумя рядами цифр более наглядно выражено на рис. 11.

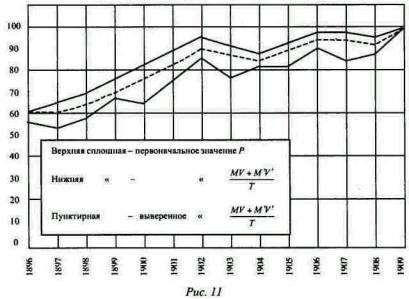
Оба значения, как указывают нижняя и верхняя кривые, совпадают одно с другим замечательно хорошо [Промежуточная кривая на рис. 11 будет объяснена ниже. ]. Точность их соответствия может быть выражена различными путями. Один путь - это сосчитать случаи совпадения и несовпадения в изменении направления или отклонения кривых. Из 12 отклонений в каждой кривой мы имеем 6 случаев совпадения, 3 случая несовпадения и 3 случая нейтральных. Другой способ сравнения был применен проф. Pearson'ом. Этот метод заключается в вычислении величины, которую проф. Pearson называет коэффициентом корреляции. Этот метод указывает на 97% совпадении, что дает преимущество против 23%, найденных проф. Pearson'OM из Дортмута для цифр [См. “Quantity Theory as tested by Kemmerer” // Quarterly Journal of Economics, 1907 - 1908. P. 287. ] проф. Kenunerer'a за 1879 - 1901 гг. Но как уже было указано, коэффициент корреляции для последовательных данных может ввести в заблуждение. Если, как в случае с цифрами проф. Kemmerer'a, коэффициент 0,23 был недостаточным подтверждением параллелизма между его кривыми, то коэффициент 0,97 преувеличивает параллелизм между нашими кривыми. Это преувеличение обычно имеет место тогда, когда обе сравниваемые кривые быстро повышаются или понижаются [Persons исчисляет коэффициент корреляции между цифрами Kemmerer'a для банковских резервов и денег в обращении, включающих банковские резервы, в 0,98, хотя эти две величины не обнаруживают сколько-нибудь значительного соответствия между колебаниями в последовательные годы, но только общее соответствие в том факте, что обе быстро падают. Коэффициент для Р, по исчислениям проф. Kemmerer'a, будет гораздо выше, если вместо того чтобы брать период начиная с 1879 г., который заключает в себе много годов, когда цены значительно изменялись, взять период, начиная с того года, которым начинаем мы, т. е. с 1896-го. Коэффициент корреляции для цифр проф. Kemmerer'a (за 1896 - 1908 гг.) равен 83%; он гораздо выше того, который получен проф. Persons'ом для периода, начинающегося с 1876 г.].

Надлежащим методом применения коэффициента корреляции к последовательным данным является, по-видимому, тот, где этот коэффициент вычисляется не для абсолютных чисел, а для последовательных из года в год отношений этих цифр. Другими словами, мы должны составлять таблицы и сравнивать ежегодно отношения значения Р для каждого года к его значению для предыдущего года и отношение значения (MV+M'V')/T для каждого года к значению (MV+M'V')/T для предыдущего года. Если оба ряда отношений будут повышаться или понижаться одновременно, то кривые будут указывать полный параллелизм или совпадение в последовательных изменениях направления. Фактически результаты этого метода указывают, что коэффициент корреляции равен 57% (или 0,57±0,10, где 0,10 есть величина вероятной ошибки). Цифра 57% есть относительно высокий коэффициент корреляции [Например, никто не будет отрицать, что длина и ширина ореха очень сильно согласованы. Коэффициент их корреляции равен 0,57. Вышина человека и ширина его фигуры коррелируют в размере 35%. ]. Следовательно, мы можем заключить, что “количественная теория” статистически проверена до высокой степени корреляции [Случайно мы можем сравнить здесь относительную степень корреляции цифр проф. Kemmerer'a с нашими цифрами. Для этой цели мы возьмем период 1896 - 1908 гг., который является длиннейшим периодом, общим обоим исследованиям. Для этих годов коэффициент наших цифр равен 54% (или 0,54±0,11) против 37% (или 0,37±0,14) для цифр проф. Kemmerer'a. Эти результаты получены методом исчисления последовательных ежегодных отношений. При методе абсолютных чисел корреляция моих данных равна 95%, а данных проф. Kemmerer'a - 83%. ].

Здесь надо отметить, что только что приведенные коэффициенты корреляции сравнивают уровень цен с тем, каким он был бы согласно статистическому значению пяти величин уравнения обмена, от которых он зависит по так называемой количественной теории. Корреляция была бы меньше, если бы вместо пяти величин была взята только одна. Так, например, коэффициент корреляции для 1896 - 1909 гг. между количеством денег М и ценами Р при методе последовательных из года в год отношений дает 43% (или 0,43±0,13) [При непосредственном (неправильном) сравнении М и Р коэффициент корреляции для 1896 - 1909 гг. будет 97%.]. Но даже и эта цифра является умеренно высокой степенью корреляции.

Если противники количественной теории, которые пытаются опровергнуть всякую связь между деньгами и ценами, указывая на отсутствие соответствия между статистическими данными этих двух факторов, подразумевают только, что другие факторы, кроме денег, а именно M', V, V', Т, меняются от времени до времени и что поэтому уровень цен фактически изменяется не в точном параллелизме с количеством денег, то их утверждение является разумным. Но приведенное положение имеет столь же малое,научное значение, как положение, что атмосферное давление не изменяется изо дня в день в точном соотношении с плотностью атмосферы. Мы знаем, что если температура остается неизменной, то давление газа изменяется прямо пропорционально его плотности, но фактически температура редко остается неизменной. Всякий критик, который пытался бы опровергнуть закон Бойля на этом основании, только обнаружил бы свое невежество в понимании действительного значения этого научного закона, а если бы серьезно пытался “опровергнуть его статистическим путем”, вычерчивая ежедневные кривые барометрического давления и плотности атмосферы, он поставил бы себя как ученого в смешное положение.

Но если бы кто-нибудь действительно представил себе, что уровень цен зависит исключительно от количества денег, то его, наверно, поправили бы. Но действительно важный вопрос, который изучающие экономику должны понять, это существование закона прямой пропорциональности между количеством денег и уровнем цен, - закона столь же реального, столь же важного и столь же основного в экономической теории денег, насколько закон Бойля о прямой пропорциональности между плотностью и давлением атмосферы является реальным, важным и основным законом в физической теории газов. Я думаю, что частые неудачи в попытках обнаружить существование этого закона обязаны в широкой мере недостатку ясного представления об относящихся сюда величинах. По-видимому, М и Р являются существенными величинами, действительный смысл которых понятен некоторым исследователям. M', V, V' и T редко обсуждаются или даже упоминаются. Но только когда этот вопрос будет поставлен на статистическое основание, в цифрах, измеряющих действительное депозитное обращение, скорости обращения и объем торговли, эти величины будут признаны имеющими реальное существование и значение.

Но непредубежденному уму количественная теория в том смысле, в котором мы ее приняли, должна представиться достаточно надежной и без такого рода проверки. Ее лучшим доказательством всегда должно быть априорное, не в том смысле, какой прилагается к доказательству абстрактных математических предложений, но в том смысле, какой прилагается к доказательству закона Бойля. Так, например, известно индуктивным путем, что давление газа в замкнутом пространстве вызывается бомбардированием его молекул в замыкающие его стенки. Равным образом известно индуктивным путем, что давление должно быть пропорционально частоте толчков при предположении, что скорости движения молекул постоянны. Наконец, известно, что частота толчков должна быть пропорциональна количеству молекул, т.е. плотности газа, и что постоянство скорости предполагает постоянство температуры. Из этого следует, что при постоянной температуре давление пропорционально плотности. Таким образом, из результатов, выведенных индуктивным методом, о единичных давлениях молекул, составляющих газ, мы можем вывести дедуктивным путем закон давления газа в целом.

Аналогично из индуктивно полученного знания об отдельных случаях обмена, принимая их как бы за молекулы, которые составляют в совокупности обмен в данном обществе, мы можем дедуктивным путем вывести общее уравнение обмена.

К счастью, точно так же, как закон Бойля был установлен и дедуктивно и индуктивно, мы можем утверждать теперь, что уравнение обмена было достаточно установлено и дедуктивно и индуктивно.

Как раньше было замечено, установление уравнения обмена не является еще в полной мере установлением количественной теории денег, так как уравнение обмена не выясняет, которые из факторов являются причиной, которые следствием. Но на этот вопрос был уже дан ответ в главе VIII.

Поправочные разницы

Теми, кто поверил априорному доказательству уравнения обмена, реальное значение замечательного совпадения в наших статистических выводах должно быть понято не как подтверждение правильности уравнения при помощи цифр, но, наоборот, как подтверждение правильности цифр при помощи уравнения. В нашей индуктивной проверке встречаются несовпадения, но все они не выходят за пределы погрешностей измерения. Эти несовпадения указывают, что в цифрах существуют незначительные ошибки, в противном случае эти цифры совершенно точно согласовывались бы с соотношением, указываемым уравнением обмена.

Нашей дальнейшей задачей является исследование этих неcовпадений и, насколько возможно, локализация встречающихся ошибок. Степень общей взаимной несогласованности между независимо вычисленными величинами лучше всего выражается степенью неравенства между вычисленными значениями величин (MV+M'V') и РТ, которые должны бы быть равны друг другу, т. е. РТ, деленное на (MV+M'V'), должно всегда равняться 1. Действительное деление дают цифры в столбце 2, озаглавленном “Первоначальное значение”, в следующей таблице. Столбец 3 будет объяснен ниже.

Вычисленное отношение РТ к (MV+M'V')

Год (1)	Первоначальное значение (2)	Уменьшенное значение (3)
	1.17	1,06
	1,24	1,13
	1,18	1,07
	1,06	0,95
	1,17	1,06
	1,11	1,00
	1,08	0,97
	1,16	1,05
	1,06	0,95
	1,09	0,98
	1,08	0,97
	1,13	1,02
	1,05	0,94
	1,00	0,89

Цифры в столбце втором показывают, что вычисленные значения РТ бывают всегда больше, чем вычисленные значения MV+M'V', причем излишек колеблется от 24% до 0 при средней величине 11%.

Но эти расхождения между РТ и (MV+M'V') могут быть в значительной степени уменьшены одним только изменением основания измерения цен. Исходной величиной, которую мы до сих пор принимали, был уровень цен 1909 г. Но поскольку index numbers'ы имеют только относительные значения, мы считаем себя свободными в выборе другого ряда чисел, содержащего также относительные величины. В силу этой прерогативы мы решили уменьшить все числа для Р на 11%, т. е. на среднюю величину первоначального расхождения. Результатом является уменьшение РТ на 11%, и таким образом изменяется ряд расхождений, показанных в столбце 2, в (приблизительный) ряд чисел, показанных в столбце 3. Эти числа колеблются в пределах от 13% выше единицы и до 11% ниже единицы. Эти ошибки очень незначительны, фактически гораздо меньше тех, которых можно было ожидать ввиду неполноты и неточности некоторых наших данных.

Остается вопрос: на чей счет мы отнесем вину за ошибки, на которые указывают имеющиеся небольшие расхождения? Будет ли это вина М, M', V, V', Р или T? Как мы будем исправлять вычисленные нами цифры? Мы можем ограничиться общими принципами, что наименьшие исправления, всего вероятнее, будут самыми правильными. Наименьшие исправления включают взаимное согласование между всеми шестью факторами, а каждое отдельное согласование будет уменьшать существующее несоответствие. Таким путем каждый вычисленный фактор рассматривается как имеющий некоторое значение и оказывающий некоторое влияние на исправление всех остальных; таким образом, каждый отдельный фактор будет требовать чрезвычайно мало изменений. Произведенные в различных факторах изменения сделаны пропорционально предполагаемой относительной их подверженности ошибкам.

Результаты этих исправлений показаны ниже, на рис. 12, 13 и 14, и на предыдущем рис. 11. Каждый из этих рисунков относится к одному из факторов уравнения обмена, как непосредственно вычисленному, так и окончательно согласованному (пунктирные линии). Если же все факторы согласованы между собой таким образом, то они вполне соответствуют уравнению обмена.

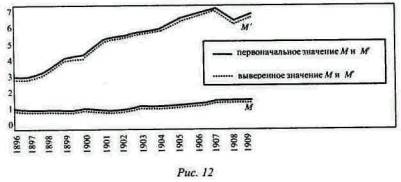
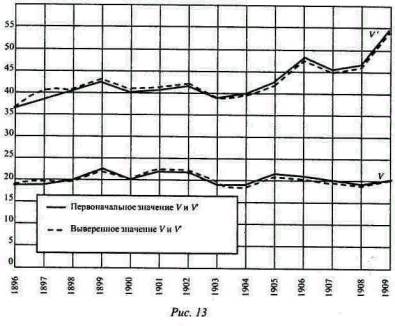
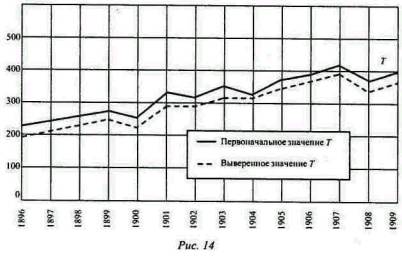
На рис. 12 мы видим, что изменения, сделанные в цифрах для М и M', так ничтожны, что ими почти можно пренебречь, так как они обычно много меньше 1%. Изменения для V и V', показанные на рис. 13, несколько больше, но тоже малы, так как обычно не достигают 2%. Изменения для T, как показано на рис. 14, хотя немного больше, чем предыдущие, но тем не менее настолько малы и однообразны, что все время сохраняют почти полный параллелизм между первоначально вычисленными и измененными кривыми. Разница редко превышает 10%. Изменения для Р показаны на приведенном выше рис. 11; верхняя кривая представляет первоначальные, а пунктирная средняя кривая - измененные величины. Чрезвычайно тесный параллелизм между первоначальной и измененной кривыми здесь также очевиден. Разница редко превышает 3%.

Конечно, самый взыскательный критик не мог бы требовать большей точности результатов и соответствия их с теорией уравнения обмена, чем показывают приведенные нами статистические данные. Исправления, которые нужно было сделать для того, чтобы привести к совершенному согласованию первоначально вычисленные шесть величин, значительно меньше вероятных ошибок в этих самых цифрах. Еще не зная, насколько окончательные результаты будут гармонировать, я сделал некоторые приблизительные вычисления вероятных ошибок. Вероятная ошибка для М оказалась 2 или 3%, для M' - 2 или 3, для V - от 5 до 10, для V' - от 5 до 10 и для Т - от 5 до 10%. Иначе говоря, наши статистические данные рассматривались только как грубые и приблизительные, однако окончательное “излечение”, необходимое для согласования их между собой, как мы видели, редко превышало 2%, будучи меньше 1% для М и М', меньше 2% для V и V', меньше 3% для Р и меньше 4% для Т. Таким образом, мы можем заключить, что цифры подходят друг к другу ближе, чем этого можно было ожидать ввиду известной их неточности.

Исправления, произведенные нами в различных факторах, настолько незначительны, что было бы рискованным пытаться специфически объяснить их. Ошибки, которые в них, вероятно, встречаются, могут происходить от многочисленных причин, как, например, от изменения соотношения между переводными и обычными чековыми сделками в Нью-Йоркской расчетной палате, или от ошибок и неточности и неполноты в статистических данных о торговле зерном и т.д., или от ошибок в виде переоценок или недооценок отклонения от нормы тех особых дней в 1896 и 1909 гг., в которые были собраны статистические данные о депозитах, сделанных в банки, или же от переоценки или недооценки депозитов, о которых не было получено сведений, или еще от недооценки или переоценки золота в Соединенных Штатах, или от недооценки или переоценки заработной платы и многих других более мелких, но часто показательных элементов в наших вычислениях.

Источники только что перечисленных ошибок были названы в порядке их вероятной важности. Может быть, знаменательно, что наибольшие расхождения приходятся на 1896 - 1898 гг., когда данные для Т были наиболее дефективны, и на 1900, 1903 и 1907 гг., которые были годами кризисов или годами приближения кризисов.

Конечные результаты

Произведя вышеуказанные взаимные согласования шести величин уравнения обмена, мы получаем следующие цифры, образующие нашу окончательную таблицу значений для М, М', V, V', Р и Т. Это цифры, нанесенные пунктирными кривыми в приведенных выше диаграммах.

Окончательно согласованные значения элементов уравнения обмена

Год	М	М'	V	V’	Р	Т	MV	M'V'	(МV+М'V') н РТ
	0,88	2,71	18,8	36,6	60,3
	0,90	2,86	19,9	39,4	60,4
	0,97	3,22	20,2	40,6	63,2		20-	131-
	1,03	3,88	21,5	42,0	71,6
	1,18	4,44	20,4	38,3	76,5
	1,22	5,13	21,8	40,6	80,5
	1,25	5,40	21,6	40,5	85,7
	1,39	5,73	20,9	39,7	82,6
	1,36	5,77	20,4	39,6	82,6
	1,45	6,54	21,6	42,7	87,7		31+	279+
	1,58	6,81	21,5	46,3	93,2
	1,63	7,13	21,3	45,3	93,2
	1,62	6,57	19,7	44,8	90,3
	1,61	6,68	21.1	52,8	100,0
	1,69	7,23	21,0	52,7	104,0
	1,64	7,78	21,0	49,9	102,2
	1,71	8,17	22,0	53,4	105,3

Эта таблица, объединяющая все независимые вычисления М, М', V, V', Р, Те исправлениями каждого из них, необходимыми для согласования со всеми другими, может считаться дающей наилучшие из имеющихся данные, касающиеся этих величин.

Эти цифры, как и пунктирные линии предыдущих диаграмм, указывают, что количество денег в обращении (М) приблизительно удвоилось в течение 13 лет, что скорость их обращения (V) увеличилась только на 10%; что количество депозитного обращения почти утроилось, а скорость его обращения (V') увеличилась на 50%; что объем торговли удвоился, а цены возросли на 2/3.

Эти выводы не поразительны, но, полагаю, как раз таковы, как мы могли ожидать. Тем не менее почти все они новы. Цифры количества денег в обращении (М) немногим отличаются от тех, которые мы находим в официальных документах и которые приведены проф. Kemmerer'ом. Точно так же цифры index numbers'ов цен основаны главным образом на index numbers'ax оптовых цен “United States Labor Bureau” и чрезвычайно сходны с ними. Статистические данные для объема торговли сконструированы совершенно заново и несколько отличаются от данных проф. Kemmerer'a, являющихся их единственным предшественником. Статистические данные для депозитов (М'), подлежащих чековому обороту, опубликованы здесь впервые. Статистические данные для скорости обращения банковских депозитов (V') являются первыми данными такого рода, исключая имеющиеся уже статистические данные для подвижности банковских счетов европейских банков. Наконец, статистические данные для скорости обращения денег являются первыми в своем роде. При помощи этих данных мы в состоянии нарисовать достаточно точную статистическую картину циркуляторной системы Соединенных Штатов. Согласно отчетам за 1909 г., количество денег в действительном обращении (М) равно 1,6 млрд, долл., или 18 долл. per capita (что гораздо меньше официальных данных о величине обращения, дающих цифру 35 долл.); скорость обращения денег (V) составляет 21 оборот в год: депозитное обращение (М') равняется 6,7 млрд. долл., или 74 долл. per capita, т. е. в 4 раза больше денежного; скорость обращения депозитов (V') составляет 53 оборота в год, т. е. в 2 1/2 раза больше скорости денежного обращения; общая сумма обращения денег или денежных платежей (MV) равна 34 млрд. в год; обращение депозитов или сумма платежей при помощи чеков (M'V') равна 353 млрд., т. е. в 10 раз больше суммы денежных платежей и составляет около 1 млрд. в день. Это дает общий итог торговых сделок, совершенных по существующим ценам, (MV+M'V') или РТ, - 387 млрд., т. е. больше чем 1 млрд. в день. Величина этой суммы, вероятно, изумит большинство наших читателей. При отсутствии прямых статистических данных мы до сих пор не могли учесть огромных размеров нашей торговли. Вероятно, немногие люди, стоящие далеко от статистики, представляли себе, что наша импортная и экспортная торговля, которая занимает такое значительное место в нашем политическом представлении, оказывается чрезвычайно незначительной в сравнении с внутренней торговлей нашего государства. Общая сумма экспорта и импорта, достигающая только 3 млрд. долл., является жалкой величиной по сравнению с общей суммой национальной торговли, составляющей 387 млрд. в год.