Метод дисконтирования и наращения

В оценке денежных потоков

Решения финансового характера в подавляющем большинстве случаев не являются одномоментными в плане проявления вызывае­мых ими последствий. Иными словами, здесь весьма важную, если не решающую, роль играет фактор времени. Формализованная осно­ва подобных решений — так называемые финансовые вычисления, имеющие давние традиции, в том числе и в отечественной учетно-аналитической практике. Финансовые вычисления базируются на понятии временной ценности денег; именно с их помощью удается принимать управленческие решения, эффективные во временном аспекте.

Ключевыми моментами методов оценки эффективности финансовых операций, определяющими их логику, являются следующие утверждения:

- практически любую финансово-хозяйственную операцию можно выразить в терминах финансов;

- в подавляющем большинстве случаев собственно операции или их последствия «растянуты» во времени;

- с каждой операцией можно увязать некоторый денежный поток;

- денежные средства должны эффективно оборачиваться, т. е. с течением времени приносить определенный доход;

- элементы денежного потока, относящиеся к разным моментам времени, без определенных преобразований несопоставимы;

- преобразования элементов денежного потока осуществляются путем применения операций наращения и дисконтирования;

- наращение и дисконтирование могут выполняться по различным схемам и с различными параметрами.

Логика построения основных алгоритмов достаточно проста и основана на двух операциях — наращении и дисконтировании. В первом случае движутся от «настоящего» к будущему, во втором — на­оборот. В обоих случаях с помощью схемы сложных процентов удается получить оценку денежного потока с позиции будущего или «настоящего». (Термин «настоящее» приводится в кавычках, поскольку он является условным, не подразумевающим обязательности связи с текущим моментом времени.)

Расчет наращенной (FV) и дисконтированной (PV) величин осу­ществляется по формулам:

FV = РV х (1 + r)ⁿ = PV xFM₁, (2.1)

где FV — наращенная сумма, т. е. доход, планируемый к получению в п-омгоду; PV — инвестируемая сумма; г — ставка наращения.

PV = FV/(1+r)ⁿ = FV x FM₂ (2.2)

где: FV— доход, планируемый к получению в n-м году; PV — приведенная (сегодняшняя, текущая) стоимость, т. е. оценка величины FV спозиции текущего момента или момента, на который осуществляется дисконтирование; r — ставка дисконтирования.

Множитель FM₁называется мультиплицирующим множите­лем для единичного платежа, а его экономический смысл состоит в следующем: он показывает, чему будет равна одна денежная еди­ница (один рубль, один доллар, одна иена и т. п.) через п периодов при заданной процентной ставке r.

Множитель FM₂ называется дисконтирующим множителем для единичного платежа, а его экономический смысл заключается в следующем: он показывает «сегодняшнюю» цену одной денежной единицы будущего, т. е. чему с позиции текущего момента равна одна денежная единица (например, один рубль), циркулирующая в сфере бизнеса п периодов спустя от момента расчета, при задан­ных процентной ставке (доходности) r и частоте начисления процен­та. Термин «сегодняшняя стоимость» не следует понимать букваль­но, поскольку дисконтирование может быть выполнено на любой мо­мент времени, необязательно совпадающий с текущим моментом.

Оценка денежного потока может выполняться в рамках решения двух задач: (а) прямой, т. е. проводится оценка с позиции будущего (реализуется схема наращения); (б) обратной, т. е. проводится оцен­ка с позиции настоящего (реализуется схема дисконтирования).

Прямая задача предполагает суммарную оценку наращенного де­нежного потока, т. е. в ее основе лежит будущая стоимость. В част­ности, если денежный поток представляет собой регулярные начис­ления процентов на вложенный капитал (Р) по схеме сложных про­центов, то в основе суммарной оценки наращенного денежного потока лежит формула 2.1.

Несложно показать, что будущая стоимость исходного денежного потока постнумерандо FV_pst может быть оценена как сумма наращен­ных поступлений, т. е. в общем виде формула имеет вид:

FV_pst= ∑C_k(1+r)^n-k, (2.3)

где n – продолжительность проекта; k - порядковый номер периода.

Обратная задача предполагает суммарную оценку дисконтирован­ного (приведенного) денежного потока.

Поскольку отдельные элементы денежного потока генерируются в различные временные ин­тервалы, а деньги имеют временную ценность, непосредственное их суммирование невозможно. Основным результатом расчета является определение общей величины приведенного денежного потока. Используемые при этом расчетные формулы различны в зависимости от вида потока — пост­нумерандо или пренумерандо. Именно обратная задача является ос­новной при оценке инвестиционных проектов.

В частности, приведенная стоимость денежного потока постнуме­рандо PV_pst в общем случае может быть рассчитана по формуле:

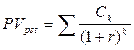(2.4)

Для потоков пренумерандо:

FV _pre = FV_post x (1+r), (2.5)

PV _pre = PV_post x (1+r) . (2.6)

Одним из ключевых понятий в финансовых и коммерческих рас­четах является понятие аннуитета. Логика, заложенная в схему ан­нуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инвестиционных проектов, а так­же в анализе аренды [27].

Аннуитет представляет собой частный случай денежного потока. Известны два подхода к его определению. Согласно первому подхо­ду аннуитет представляет собой однонаправленный денежный поток, элементы которого имеют место через равные временные интервалы.

Второй подход накладывает дополнительное ограничение, а именно: элементы денежного потока одинаковы по величине.

Если число равных временных интервалов ограничено, ан­нуитет называется срочным:

С₁ = С₂ = ... = Сп = А.

Для оценки будущей и приведенной стоимости аннуитета можно пользоваться вышеприведенными формулами, вместе с тем благода­ря специфике аннуитетов в отношении равенства денежных поступ­лений они могут быть существенно упрощены.

В частности, для решения прямой задачи оценки срочных аннуи­тетов постнумерандо и пренумерандо при заданных величинах регу­лярного поступления (А) и процентной ставке (r) можно воспользо­ваться формулами:

FV^a_pst = A x FM₃(r; n), (2.7)

FV^a_pre = FV^a_pst x (1+r) = A x FM₃(r; n) x (1+r), (2.8)

где FM₃(r; n) =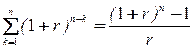

Экономический смысл мультиплицирую­щего множителя FM₃(r; n) для аннуитета заключается в следующем: он пока­лывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия.

Для решения обратной задачи оценки срочных аннуитетов постну­мерандо и пренумерандо, являющейся основной при анализе инвести­ционных проектов, денежные притоки которых имеют вид аннуитет­ных поступлений, можно воспользоваться формулами:

PV ^a_pst = A x FM₄(r; n), (2.9)

PV ^a_pre = PV ^a_pst x FM₄(r; n) x (1+r), (2.10)

где FM₄(r; n) = .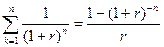

Экономический смысл дисконтирующего множителя FM₄(r; n) для аннуитета заключается в следующем: он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы (наприме, один рубль), продолжающегося п равных периодов с заданной процентной ставкой r.

При выполнении некоторых инвестиционных расчетов используется техника оценки бессрочного аннуитета. Аннуитет называется бессрочным, если денежные поступления продолжаются достаточно длительное время (в западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет).

В этом случае прямая задача смысла не имеет. Что касается обратной задачи, то ее решение для аннуитета постнумерандо делается на основе формулы:

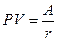. (2.11)

Приведенная формула используется для оценки целесообразности приобретения бессрочного аннуитета. В этом случае известен размер годовых поступлений; в качестве коэффициента дисконтирования обычно принимается гарантированная процентная ставка (например, процент, предлагаемый государственным банком).