Текущая доходность облигации
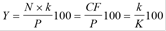
Накопленный купонный доход
➨ Если облигация приобретается между купонными
выплатами, важную роль в анализе имеет накопленный
купонный доход
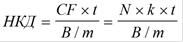
Доходность облигации к погашению (Yield To Maturity - YTM)
➨Годовая ставка сложных процентов, которая
уравнивает рыночную стоимость облигации и
современную стоимость генерируемого ей потока
платежей.
Подразумевает, что:
➨облигация хранится до погашения
➨все платежи будут осуществлены
➨купонные выплаты реинвестируются по YTM
Доходность облигации к погашению (YTM)
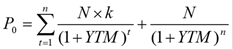
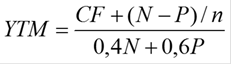
Взаимосвязь между ставкой купона k, доходностью
к погашению YTM и ценой облигации Р
➨Если P > N, k > YTM
➨Если P < N, k < YTM
➨Если P = N, k = YTM
Взаимосвязь между ценой облигации Р, ставкой
купона k и доходностью к погашению YTM
➨Если YTM > k, P < N
➨Если YTM < k, P > N
➨Если YTM = k, P = N
➨Если рыночный курс облигации Р растет, то ее
доходность к погашению YTM должна падать и
обратно
➨Уменьшение доходности облигации приведет к
росту ее курса на величину большую, чем
соответствующее падение курса при увеличении доходности на ту же величину
Взаимосвязь между ценой облигации Р и
сроком погашения n
➨Если YTM > k, сумма дисконта уменьшается при
приближении к сроку погашения
➨Если YTM < k, величина премии будет
уменьшаться при приближении к сроку погашения
➨Чем больше срок погашения, тем чувствительнее
ее цена Р к изменениям YTM
Дюрация и ее интерпретация
➨Средний срок погашения обязательства
➨Средняя продолжительность (момент) выплат
➨Средний срок связывания средств в активе
➨Средний срок окупаемости инвестиций
➨Математическое ожидание среднего срока
погашения / момента выплат
➨Дюрация является эластичностью цены по
отношению к изменению доходности
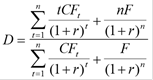
Свойства дюрации
➨Дюрация купонной облигации всегда меньше
срока ее погашения
➨Дюрация дисконтной облигации равна сроку ее
погашения
➨Чем выше доходность к погашению, тем меньше
дюрация обязательства
Предельная величина дюрации
➨При стремление срока погашения к бесконечности
дюрация стремится к пределу
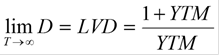
Зависимость между дюрацией, сроком
погашения и ценой
➨ дюрация купонной облигации, стоимость которой
больше или равна номиналу, монотонно возрас-
тает вместе с увеличением срока погашения и
приближается к своему предельному значению –
LVD, по мере приближения срока погашения к
бесконечности, т.е. при n →, D →LVD;
➨ дюрация купонной облигации, стоимость которой
ниже номинала (т.е. приобретаемой с дисконтом),
достигает своего максимума прежде срока пога-
шения n и затем снижается по направлению к
величине LVD.
