Алгебра высказываний. Основные логические операции

Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются понятие, высказывание, умозаключение.

Понятие– это форма мышления, фиксирующая основные, существенные признаки объекта.

Высказывание– это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.

Умозаключение– это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

Объектами алгебры высказываний являются повествовательные предложения, относительно каждого из которых имеет смысл говорить истинно оно или ложно. Такие предложения называются простыми высказываниями. Например: «Липецк – город металлургов» - истинное высказывание, «Минск – столица Украины» - ложное высказывание.

В алгебре высказываний высказывания обозначаются именами логических переменных: А=1 (если высказывание истинно), А=0 (если высказывание ложно).

Высказываниями не являются, например, предложения “ученик десятого класса” и “информатика — интересный предмет”. Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие “интересный предмет”. Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.

Над высказываниями можно производить определенные логические операции, в результате чего получаются новые, составные высказывания. К таким логическим операциям относятся: логическое умножение (конъюнкция), логическое сложение (дизъюнкция), логическое отрицание (инверсия).

1. Операция, выражаемая связкой “и”, называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается знаком & (может также обозначаться знаками ^ или •). Высказывание А & В истинно тогда и только тогда, когда оба высказывания А и В истинны.

2. Операция, выражаемая связкой “или” (в неразделительном, неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком v или +). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.

3. Операция, выражаемая словом “не”, называется отрицанием и обозначается чертой над высказыванием. Высказывание не A истинно, когда A ложно, и ложно, когда истинно.

Порядок выполнения логических операций: сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после дизъюнкция (“или”). Круглые скобки меняют приоритетность выполнения операции.

Ложное высказывание (или операция) обозначается 0 (ЛОЖЬ, FALSE)

Истинное высказывание (или операция) обозначается 1 (ИСТИНА, TRUU)

Тогда таблица истинности приобретает некий арифметический вид.

A	B	AΛB	AVB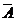

В алгебре высказываний суждениям ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита.

Логическая функция - это функция логических переменных, которая может принимать только два значения : 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, т.е. заменить логической функцией. Обычно значения логических функций записываются в виде таблиц (т.н. таблицы истинности). Число строк в такой таблице - это число возможных наборов значений аргументов. Оно равно 2ⁿ, где n - число переменных. Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Пример 1. Для формулы 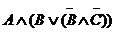построить таблицу истинности.

Решение

Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2³=8.

Количество логических операций в формуле 5, следовательно, количество столбцов в таблице истинности должно быть 3+5=8.

A	B	C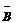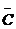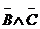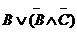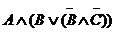

Законы алгебры логики

Законы алгебры логики отражают наиболее важные закономерности логического мышления. Представлены они в виде формул и позволяют производить тождественные преобразования логических выражений.

Закон тождества. Всякое высказывание тождественно самому себе: А = А.

Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. А & 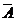= 0.

Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. А v 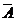= 1.

Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание. 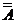= А.

Законы де Моргана. = &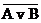

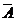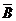
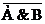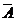= v .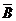

Следующие три закона имеют аналоги в обычной алгебре.

Закон коммутативности. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:

А & В = В & А А v В = В v А.

Закон ассоциативности. Если в логическом выражении используются только операции логического сложения или логического умножения, то можно пренебрегать скобками или произвольно их расставлять:

(А & В) & С = А & (В & С) (А v В) v С = А v (В v С).

Закон дистрибутивности. Этот закон позволяет выносить за скобки как общие множители, так и общие слагаемые:

(А & В) v (А & С) = А & (В v С) (А v В) & (А v С) = А v (В &С).

Закон поглощения. A v (B & A) == A A & (B v A) == A