Значення операції визначення поняття

Завдяки операції визначення поняття розкривають його зміст і в такий спосіб з'ясовують істотні й загальні властивості відповідних предметів та їх імена. Це дає можливість відрізняти мислимі в понятті предмети від усіх інших, навіть подібних, від яких вони відрізняються принаймні деякими істотними властивостями.

Поняття є результатом тривалого процесу пізнання, його підсумком. Як своєрідні «комори знань», воусією відповідальністю, що «демократія» не належить до понять фізики». Оскільки це судження містить гранично бідну інформацію, воно не може вважатися визначенням. Хоча звідси не випливає, що будь-яке заперечне судження не може відігравати роль визначення. Як відомо, математичні науки іноді вдаються до заперечних визначень.

Діяти доводиться за відсутності понятійного знання про предмети, тому звертаються й до інших засобів пізнання, які лише нагадують визначення понять. Йдеться насамперед про характеристику, портрет, опис, порівняння, вказівку тощо.

До перелічених засобів іноді звертаються і за умови наявності поняття про відповідний предмет. Річ у тім, що в деяких практичних ситуаціях не обійтися без знань неістотних властивостей пізнаваних предметів, які, не відображаються в поняттях. Спробуйте розпізнати людину, яку потрібно зустріти, скажімо, на вокзалі великого міста, маючи про неї лише поняття, тобто знаючи лише істотні й загальні ознаки. В той же час знання неістотних ознак — статі, віку, специфіки зовнішності, одягу і навіть речей, які вона матиме, — дадуть змогу її впізнати.

Чим же відрізняється визначення поняття від перелічених засобів пізнання? У понятті, як відомо, відображаються істотні, загальні ознаки предметів і явищ, а в перелічених засобах пізнання можуть розкриватися як істотні, так і неістотні ознаки. Щоправда, в одних із названих засобів пізнання акцент робиться на істотних ознаках (характеристика), в других — як на істотних, так і на неістотних (портрет, опис), а в третіх, — як правило, на неістотних ознаках.

Значення операції визначення поняття

Завдяки операції визначення поняття розкривають його зміст і в такий спосіб з'ясовують істотні й загальні властивості відповідних предметів та їх імена. Це дає можливість відрізняти мислимі в понятті предмети від усіх інших, навіть подібних, від яких вони відрізняються принаймні деякими істотними властивостями.

Поняття є результатом тривалого процесу пізнання, його підсумком. Як своєрідні «комори знань», вони тривалий час формуються і наповнюються. Деякі з понять мають багатотисячну історію формування. Прикладом таких понять можуть бути категорії матерії та свідомості (духу), добра і зла, прекрасного і потворного. Завдяки все новим і новим визначенням поняття уточнюються шляхом виявлення нових істотних ознак відповідних предметів і вилучення з них неістотних.

Як не парадоксально, але потреба у визначенні понять часто виникає ще на початковому етапі пізнання відповідних предметів. Про це переконливо писав Г. Плеханов у «Листах без адреси». В таких випадках доводиться звертатися до так званих робочих визначень, які, зазнаючи певних, іноді істотних, змін у процесі наукового дослідження, набувають статусу наукових.

Важко перебільшити роль визначень понять у навчальному процесі. Так, знання тих чи інших слів, термінів ще не свідчать про наявність відповідних понять. Тому викладачам усіх дисциплін доводиться постійно перевіряти наявність понятійних знань, звертаючись до учнів з такими запитаннями: «Який зміст має поняття... (скажімо, «метафора»)?», або «Дайте визначення поняття метафори», або «Які ознаки мисляться в понятті «метафора»?», або «Що таке метафора?», «Що називають метафорою?».

До визначення понять час від часу змушена звертатися кожна людина.

Умовивід — це форма мислення, в якій з одного чи декількох істинних суджень на основі певних правил виводу виводять нове судження. Структура кожного умовиводу включає в себе засновки, висновок і логічний зв'язок між засновками та висновком.

Умовивід буде правильним тоді і тільки тоді, коли в ньому виконуються основні закони логіки (тотожності, несуперечності, виключеного третього, закон достатньої підстави). Логічним висновком з даних засновків є таке речення, яке не може бути хибним, коли ці засновки істинні. Умовиводи поділяються на дедуктивні, індуктивні та умовиводи за аналогією. Вони можуть бути необхідними та ймовірними (правдоподібними).

Дедуктивний умовивід — це умовивід, в якому висновок зроблено обов'язково із засновків, які виражають знання достатньо великого ступеня загальності і які самі є знанням меншого ступеня загальності, наприклад:

Усі ссавці годують своїх дітей молоком.

Собака — ссавець.

Отже, всі собаки годують своїх дітей молоком.

Логічне слідування іде від роду до виду, від загального класу до підкласу.

Правила виводу повинні задовольняти ряд вимог:

по-перше, з істинних засновків вони повинні дозволяти виводити тільки істинні судження;

по-друге, правила виводу повинні бути несуперечними (сумісними) в даній логічній системі, тобто неможливо одним способом з одних і тих самих засновків виводити висновок «А», а другим способом — «не-А»;

по-третє, необхідно виходити з наявності повноти системи, а це означає: користуючись тільки даними правилами виводу в даній логічній системі, можливо вивести будь-які змістово-істинні висновки, що сформульовані в термінах даної системи і логічно випливають з даних засновків.

Правила прямого виводу дозволяють з наявних істинних засновків одержати істинний висновок.

Правила непрямого виводу дають змогу робити висновок про правомірність деяких висновків з правомірності інших.

Безпосередні умовиводи — це дедуктивні умовиводи, які виводять з одного засновку. До них належать перетворення, обернення, протиставлення предикатові та умовивід за «логічним квадратом».

Перетворення — вид безпосереднього умовиводу, в якому змінюється якість засновків без зміни їх кількості.

Перетворення будуються:

1) шляхом подвійного заперечення, яке ставиться перед зв'язкою і перед предикатом (S є Р ® S не є не-Р);

2) шляхом перенесення заперечення з предиката до зв'язки (S є не-Р ® S не є Р).

Приклад перетворення:

Деякі держави є федераціями. ($S – Р)

Деякі держави не є нефедераціями. ($S~ù P)

Оберненням називається такий безпосередній умовивід, в якому у висновку (новому судженні) суб'єктом стає предикат, а предикатом — суб'єкт. Обернення бувають прості (без обмежень) і з обмеженнями. Частковозаперечні судження не обертаються.

Прості обернення утворюються тоді, коли і S і Р вихідного судження або розподілені, або нерозподілені. Наприклад:

Деякі студенти — філателісти. ($S – Р)

Деякі філателісти — студенти. ($S~ù P)

Обернення з обмеженням можна зробити тоді, коли у вихідному судженні суб'єкт є розподіленим, а предекат — нерозподіленим, або навпаки — суб'єкт є нерозподіленим, а предикат — розподіленим. Наприклад:

Усі гітаристи — музиканти. ("S – Р)

Деякі музиканти — гітаристи. ($S ~ù P)

Протиставлення предикату — такий безпосередній умовивід, в якому в новому судженні (тобто висновку) суб'єктом виступає поняття, яке суперечить предикату вихідного судження, а предикатом є суб'єкт вихідного судження, причому зв'язка змінюється на протилежну. Алгоритмом для отримання висновку є наступні кроки:

1) перетворити засновок;

2) перетворене судження обернути.

Наприклад:

Усі вовки — хижі тварини. ("S – Р)

Усі вовки не є нехижими тваринами. ("S ~ù P)

Жодна нехижа тварина не є вовком. ("ù S ~ P)

Протиставлення суб'єкту — такий безпосередній умовивід, в якому предикат вихідного судження стає суб'єктом висновку, а предикатом висновку береться поняття, що суперечне суб'єктові засновку. При цьому якість судження завжди змінюється. Алгоритмом для отримання висновку є наступні кроки: спочатку вихідне судження обертається, а потім результат перетворюється.

Наприклад:

Деякі студенти — юристи. ($S – Р)

Деякі юристи є студентами. ($P – S)

Деякі юристи не є нестудентами. ($P ~ù S)

Безпосередній умовивід за «логічним квадратом» за сутністю є трансформацією заданого судження (засновку) у три інших судження.

Разом із засновком висновки складають 4 судження, причому два з них є істинними, і два — хибними.

Наприклад: Якщо маємо засновок А — Усяка політика є брудною справою (істинне судження), то можна отримати наступні засновки, серед котрих буде тільки один істинний (у даному випадку частковоствердне судження І):

Е — Жодна політика не є брудною справою (хибне);

І — Деяка політика є брудною справою (істинне);

О — Деяка політика не є брудною справою (хибне).

6.3. Категоричний силогізм та його різновиди. Ентимема

Категоричний силогізм — це вид дедуктивного умовиводу, в якому з двох категоричних суджень, зв'язаних середнім терміном (М), при додержанні правил обов'язково повинні бути два засновки і висновок. Поняття, що входять до складу силогізму, називають його термінами.

Більший засновок має в собі більший за обсягом термін, менший засновок — менший термін. В основі висновку в категоричному силогізмі лежить аксіома силогізму: «Все, що стверджується або заперечується стосовно виду (або члена даного класу), належить до даного роду».

Фігурами силогізму називаються форми силогізму, які розрізняються за положенням середнього терміна М у засновках і обов'язково наявністю предиката у більшому засновку і суб'єкта у меншому засновку:

S ——— P S ——— P S ——— P S ——— P

Mодусами категоричного силогізму називаються його різновиди, що відрізняються один від одного якісною та кількісною характеристикою засновків, що входять до нього, і висновком. Кожна фігура силогізму має певну кількість правильних модусів, тобто формул коректних рішень:

перша фігура — ААА, ЕАЕ, АІІ, ЕІО;

друга фігура — ЕАЕ, АОО, АЕЕ, ЕІО;

третя фігура — ОАО, ААІ, АІІ, ІАІ, ЕАО, ЕІО;

четверта фігура — ААІ, ЕАО, ІАІ, ЕОІ, АЕЕ.

Індуктивні умовиводи — це опосередковані умовиводи, в яких з одиничних суджень — засновків виводять часткове або й загальне судження — висновок. У гносеології індукцією називають метод наукового пізнання, який полягає в дослідженні процесу пізнання від одиничного до часткового або загального. Існують повна і неповна індукції. Неповна індукція у свою чергу поділяється на наукову і популярну.

Повна індукція — це різновид індуктивного умовиводу, в якому на підставі значення про належність певної ознаки кожному предметові класу робиться висновок про належність цієї ознаки всім предметам цього класу.

Умовивід за повною індукцією є необхідним, тобто його вірогідність дорівнює одиниці (Р = 1).

Неповна індукція — це індуктивний умовивід, в якому висновок про весь клас предметів робиться на підставі знання тільки деяких предметів цього класу.

Умовивід за неповною індукцією є ймовірним, тобто його вірогіднiсть менше одиниці і більше нуля (0 < P < 1)

Висновки. Умовиводи поділяються: 1) за формою міркування на дедуктивні, індуктивні, традуктивні; 2) за ступенем обґрунтованості на достовірні (необхідні) і ймовірні (правдоподібні); 3) за кількістю засновків на безпосередні і опосередковані.

	8.1. Поняття простого категоричного силогізму та його структура
Module:	Розділ 8 - Простий категоричний силогізм
Діяльність:	Лекційні матеріали

В простому категоричному силогізмі висновок є логічним наслідком з двох категоричних суджень. Наприклад:

Суверенна держава (S) має свою територію (Р).

Україна (S) – суверенна держава (Р).

Україна (S) має свою територію (Р).

Таким чином, простий категоричний силогізм складається з трьох категоричних суджень, два з яких є засновками, а третє – висновком.

В склад даного силогізму входять три поняття: “суверенна держава”, “своя територія” та “Україна”.

* Поняття, що входять до складу категоричного силогізму, називають термінами силогізму.

Серед них розрізняють менший, більший та середній терміни.

* Меншим терміномсилогізму є суб’єкт висновку.

В прикладі це поняття “Україна”.

* Більшим терміном силогізму є предикат висновку.

В прикладі це – “своя територія”. Більший та менший терміни силогізму називають крайніми термінами; їх відповідно позначають – S та Р.

Кожен із крайніх термінів входить не тільки у висновок, але й в один із засновків. Засновок, що включає менший термін, називають меншим засновком; засновок, який включає більший термін, називають більшим засновком. Більший та менший засновки можуть займати в силогізмі як перше, так і друге місце. Але розрізняють їх не за місцем в силогізмі, а за термінами, які вони включають в себе.

Висновок із засновків був би неможливим, якби в них не містився ще один термін – середній.

* Середнім терміном силогізму називають поняття, що входить до обох засновківі відсутнє у висновку

В нашому прикладі – “суверенна держава”. Середній термін позначають літерою М (від латинського medius - середній).

Середній термін пов’язує крайні терміни і робить можливим вивід. Відношення крайніх термінів (S та Р висновку) існує завдячуючи їх відношенню до середнього терміна. Поставивши в нашому прикладі на місця термінів судження терміни силогізму, отримаємо:

Суверенна держава (М) має свою територію (Р).

Україна (S) – суверенна держава (М).

Україна (S) має свою територію (Р).

Термінам категоричного силогізму можна дати об’ємну інтерпретацію через відомі вже нам кола Ейлера:

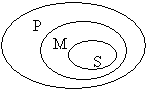
Отже,

*простий категоричний силогізм – це дедуктивний умовивід про відношення двох крайніх термінів на підставі їх зв’язку з середнім терміном.

Необхідність виводу, тобто логічного переходу від засновків до висновку в категоричному силогізмі грунтується на твердженні (аксіомі силогізму): Все, що стверджується або заперечується про всі предмети даного класу, стверджується або заперечується про кожен предмет або будь-яку частину предметів даного класу.

Так, в силогізмі:

Всі громадяни України (М) мають політичні права (Р).

Симоненко (S) є громадянином України (М).

Симоненко (S) має політичні права (Р).

Все, що стверджується відносно всіх громадян України, з необхідністю стверджується і про кожного громадянина України.

В силогізмі:

Ніхто не притягується до кримінальної відповідальності (Р) без рішення суду (М).

Відносно Симоненка (S) такого рішення немає (М).

Симоненко (S) не притягується до кримінальної відповідальності (Р).

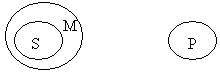
Все, що заперечується відносно всіх неосуджених громадян, заперечується і відносно кожного неосудженого громадянина.

Епіхейрема — це складноскорочений силогізм, до складу якого входять два засновки, принаймні один з яких є енти-
мемою.

Приклад: Захист прав людини — благородна справа,
оскільки він — сприяє утвердженню демократії.

Відстоювання гласності є захистом прав людини,

тому що воно сприяє утвердженню демократії.

Отже,Відстоювання гласності — благородна справа.

Логічна формула епіхейреми:	"М є Р, тому що "М є N
	"S є М, тому що "S є Q
Отже:	"S є Р
Аналіз першого засновку:	"N є P
	"М є N
	"М є Р
Аналіз другого засновку:	"Q є М
	"S є Q
	"S є М
	Висновок:	"М є Р
	"S є М
	Отже:	"S є Р

Доведення являє собою систему логічних процедур, у процесі якої істинність якого-небудь судження обґрунтовується за допомогою інших суджень, істинність яких була раніше встановлена. Іншими словами, якщо ми маємо якесь судження і не знаємо, істинне воно чи хибне, то для його перевірки ми можемо і повинні скористатися іншим судженням, істинність якого не підлягає науковому сумніву.

Доведення має таку загальну структуру: теза, аргументи (основа), демонстрація (рис. 10.1).

Рис. 10.1 − Загальна структура доведення

Таким чином, теза, аргументи, демонстрація – це три обов'язкові складові частини доведення. Відсутність хоча б однієї з них приводить наше міркування до логічних помилок, а якщо це робиться навмисно, то виникають можливості для софістичних спекуляцій.

За способом здійснення доведення може бути прямим чи непрямим.

У прямому доведенні істинність тези виводиться з істинності аргументів, тобто для підтвердження істинності тези беруться такі аргументи, аксіоми, положення, з яких аподиктично виводиться теза. Логіка прямого доведення має таку чи подібну структуру: припустимо, що основа (А, В, С, D...) з необхідністю обумовлює істинність суджень (R, F, S, Р...), а якщо так, то останні є підставою істинності тези N. Саме за такими схемами звичайно проводяться доведення в наукових дослідженнях, у дискусіях, що проводяться за правилами і законами логічного мистецтва, і викладачі викладають свій лекційний матеріал для студентів саме в такому стилі.

Однак у житті часто доводиться зустрічатися з такими ситуаціями, коли аргументів, які б безпосередньо доводили істинність певної тези, в даний момент немає.

Як же бути в такому випадку ?

Необхідно знайти таке судження, яке б суперечило тезі і при цьому було б хибним. Знайшовши такі аргументи, необхідно довести хибність судження, що суперечить тезі. Якщо ми проробимо таку логічну операцію, то підключивши до цього процесу закон виключеного третього, дійдемо висновку, що дане судження є хибним. А якщо це так, то судження, яке йому суперечить, буде істинним.

Таким чином, доведення, в якому істинність тези обґрунтовується за допомогою спростування істинності суперечного положення, називається непрямим доведенням. Можна охарактеризувати непряме доведення і по-іншому, а саме: істинність висунутої тези обґрунтовується за допомогою доведення хибності антитези.

Отже в непрямому доведенні ми припускаємо істинність судження, що суперечить тезі, а потім виводимо всі наслідки. Якщо ці наслідки будуть суперечити судженню, прийнятому нами за істинне, то ми повинні визнати, що антитеза, з якої ми вивели наслідок, є хибною. Однак якщо ми зафіксували хибність антитези, то з цього цілком природно випливає, що теза є істинною, що і треба було довести.

Що таке індуктивне доведення? Це не що інше, як індуктивний умовивід. А це значить, що індуктивне доведення повинно ґрунтуватися на аналізі й порівнянні даних спостереження чи експерименту. Важливо відзначити, що в міру нагромадження множини експериментальних даних, ми виявляємо регулярну повторюваність якихось ознак і відношень стосовно предмета чи явища, що спостерігається. Саме ця повторюваність і слугує міцною підставою індуктивного доведення висунутої тези.

Якщо множина розглядуваних альтернатив, стосовно яких необхідно довести якесь положення, є скінченною, а її розмірність не дуже великою, то доведення цього положення стосовно всієї множини можна здійснювати шляхом простого перебору кожної з її альтернатив (рис. 10.3).

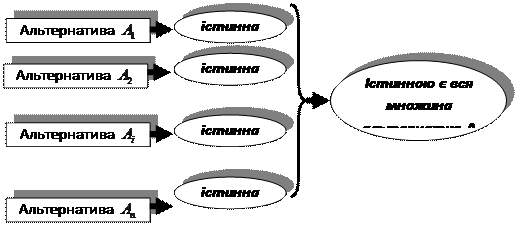Рис.10.3 − Індуктивне доведення істинності для множини

Припустимо, що нам потрібно довести таку тезу: "Усі відомі селітри добре розчиняються у воді".

Як аргументи, що доводять істинність цього положення, ми по черзі наводимо такі доводи:

Кальцієва селітра є добре розчинною у воді.

Аміачна селітра є добре розчинною у воді.

Натрієва селітра є добре розчинною у воді.

Калієва селітра є добре розчинною у воді.

Інших різновидів селітри, крім перерахованих, ми не знаємо.

Отже з наведених одиничних доводів, що вичерпують цілком поняття селітри, ми аподиктично приходимо до істинності доказуваної нами тези:

"Усі відомі селітри добре розчиняються у воді".

Дедуктивне доведення є не чим іншим, як силогізмом. Структура доведення його є такою. Ми знаходимо деяке загальне судження, в якому міститься імовірність силогістичного виведення доказуваної тези, і його істинність складає основу для визначення істинності цієї тези (рис. 10.4).

Рис. 10.4 − Схема дедуктивного доведення

Припустимо, нам необхідно довести якесь положення S-P. Для цього треба в першу чергу знайти середній термін, який би міг бути спільним для S і P, тобто бути своєрідним посередником між ними. Саме цей термін забезпечує ланцюг взаємозалежних суджень.

Припустимо, нам необхідно довести, що сигарети "Camel" є шкідливими для здоров'я людини. Ми шукаємо таке поняття, яке могло б бути середнім терміном і стосовно сигарет "Camel", і стосовно поняття "здоров'я людини". Таким може бути поняття "тютюнові вироби". Звідси ми отримуємо силогізм:

Усі тютюнові вироби за даними ВООЗ (Всесвітня організація охорони здоров'я) згубно впливають на здоров'я людини.

Сигарети "Camel" є тютюновим виробом.

Сигарети "Camel" згубно впливають на здоров'я людини.

Саме це нам і треба було довести.

Важливо підкреслити, що в наших міркуваннях дедукція й індукція завжди пов'язані між собою і являють єдиний доказовий процес. У будь-якій дедукції більший засновок силогізму – це результат індуктивного умовиводу, а це значить, що дедукція ґрунтується на індукції. Але й індукція не може обійтися без дедукції. Приміром, як сформулювати гіпотезу? Перевірка гіпотези являє собою, як це ми бачили на прикладах селітри, виведення з неї можливих наслідків. Таким чином, ми переконуємося в тому, що в доведеннях дедукція неможлива без індукції і навпаки.