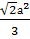Задача 2 (метод площадей).

Памятка решения геометрических задач.

1) Чтение условия задачи.

2) Выполнение чертежа с буквенными обозначениями.

3) Краткая запись условия (база знаний)

4) Деталировка – вычерчивания отдельных деталей на дополнительных чертежах; исходная сложная задача разбивается на несколько простых

5) Составление цепочки действий

6) Реализация алгоритма решения

7) Проверка правильности решения (логику доказательства, найденные величины имеют геометрический смысл)

8) Ответ

Задача 1 (медианы в треугольнике).

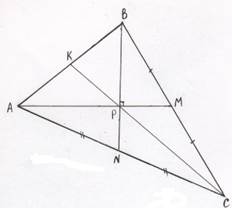
Медианы АМ и BN треугольника АВС перпендикулярны и пересекаются в точке Р.

а) Докажите, что СР=АВ.

б) Найдите S _ΔАВС, если известно, что АС=6 и ВС=7.

Повторить. 1) медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1; 2) медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине; 3) каждая медиана делит треугольник на два, равных по площади.

Решение

1) Так как медианы треугольника пересекаются в одной точке, то СР – это отрезок медианы. Пусть СР пересекается с АВ в точке К, тогда СК – медиана треугольника и СР= СК=2РК (свойство медиан)

2) РК – медиана прямоугольного треугольника АВР, поэтому РК=0,5АВ.

3) Из 1) и 2)=>АВ=2PK =СР.

Пункт а) доказан.

б) 1) Пусть ВР=2х, PN=х, АР=2у, РМ=у. Применяя теорему Пифагора для треугольников ВМР и АРN, получим систему

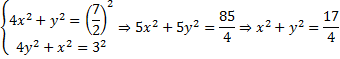
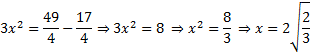
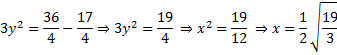
2) АМ – медиана треугольника АВC, поэтому площадь треугольника АВМ равна

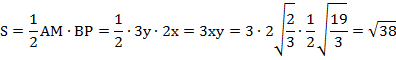
Значит, площадь треугольника АВС равна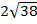

Ответ: S _ΔАВС =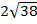

Задача 2 (метод площадей).

Окружность с центром О, вписанная в S _ΔАВС касается стороны ВС в точке Р и пересекает отрезок ВО в точке Q. Отрезки OC II QP

а) Доказать: S _ΔАВС – равнобедренный

б) Найти S _ΔBPQ, если точка О делит высоту ВН в отношении ВО: ОН=3:1, АС =2а.

Повторить. Для доказательства пункта a) необходимо вcпомнить признаки равнобедренного треугольника: если высота и биссектриса, проведенная к одной стороне, совпадают, то такой треугольник является равнобедренным.

Решение

а) 1) ΔАВС – описанный около окружности, поэтому О – точка пересечения биссектрис.

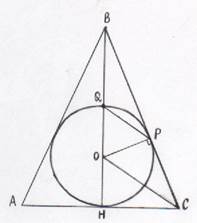
2) OP BC (радиус, проведенный в точку касания), значит ΔВРО – прямоугольный.

3) Пусть углы АСО и ВСО равны α, тогда угол СОР равен 90-α и равен углу ОРQ, так как ОС II QP, углы OPQ и COP – накрест лежащие.

ΔQOP - равнобедренный, так как OQ=OP (радиусы).
QOP = -2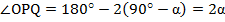

4) Пусть ВО пересекается с АС в точке Н. Рассмотрим треугольники ВОР и ВСН. У них угол при вершине В общий, 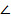ВОР= 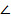ВСН=2α. Значит, ΔВОР подобен ΔВСН по двум углам. Следовательно, 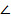ВНС= 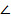ВРО=90°

5) Рассмотрим треугольник АВС. У него ВН является биссектрисой и высотой. Поэтому по признаку равнобедренного треугольника ΔАВС – равнобедренный. Пункт а) доказан.

б) При нахождении S _ΔBQP будем использовать «метод площадей»: если два треугольника имеют общий угол, то их площади относятся как произведения сторон, содержащих этот угол, то есть есл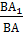и = k и 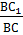= m, то 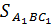= km .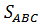

1) ΔАВС – равнобедренный (см. пункт а), ВН – высота, => ВН – медиана. Если АС = 2а по условию, то НС = а.

2) НС = СР = а (свойство отрезков касательных)

3) СО – биссектриса ΔВНС. По свойству биссектрисы треугольника 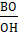= = 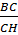3:1(по условию). Поэтому ВС=3а, тогда ВР = ВС – РС = 3а - а = 2а. С другой стороны 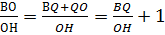= 3,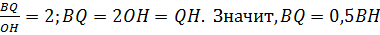

S _ΔBHC=0,5∙ ВН∙ НС =0,5 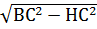∙ НС=0,5 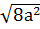∙а = а²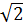

4) BQ : BH=1 : 2; BP : BC=2 : 3. Поэтому S_BQP = 0,5 ∙ = .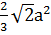

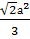Задача в пункте б) может быть решена другими способами. Например, ΔОНС и ΔВНС имеют общую высоту HС. 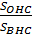= 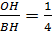. S_OPC = S_OHC. Поэтому S_BPO=0,5 S _BHC. Аналогично, S_BQP = S_BPO. Значит, S_BQP =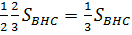

Возможно и третье решение. Из треугольника ВНС найти синус угла НВС, далее, вычислив стороны BQ и BP треугольника BQP, найти его площадь

S_{BQP =}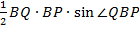

Ответ: