И подобия треугольников
Прямоугольный

 В
В
 D c
D c 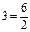
а h bc

 С α А
С α А
b
1.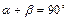 6.
6. 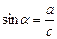
2. 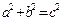 7.
7. 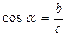
3. 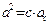 8.
8. 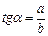
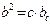 9.
9. 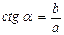
4. 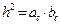 10.
10. 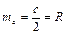
5. 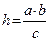

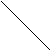



 х
х 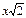
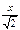 х
х
45 ۫ 45 ۫

 х
х






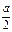 60 ۫ а
60 ۫ а 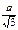
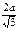

 30 ۫ 30۫
30 ۫ 30۫
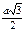 а
а
Пифагоровы тройки
(3;4;5) (5;12;13)
(ka;kb;kc) (7;24;25)
(6;8;10) (8;15;17)
(9;12;15) (9;40;41)
(12;16;20) (20;21;29)
 (15;20;25) (12;35;37)
(15;20;25) (12;35;37)
 ТРЕУГОЛЬНИКИ
ТРЕУГОЛЬНИКИ






 равнобедренный равносторонний произвольныйB β
равнобедренный равносторонний произвольныйB β





 В В а
В В а
1. a2 =b2+c2-2bc cos 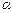 с
с
 R a 2.
R a 2. 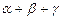 = 1800 A α b γ C
= 1800 A α b γ C



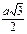 3.
3. 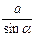 =
= 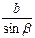 =
= 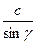 = 2R
= 2R

 А Н С A C 4. напротив большего угла лежит большая сторона
А Н С A C 4. напротив большего угла лежит большая сторона
ВН–бис.,мед., выс. R = 2 r 5. неравенство ∆: b< a+c, где b- наибольшая

 ЛИНИИ ТРЕУГОЛЬНИКА
ЛИНИИ ТРЕУГОЛЬНИКА
 |  |  |  | ||||

 медианы биссектрисы высоты
медианы биссектрисы высоты



 В В
В В
1. ортоцент

 О М о – внутри ∆
О М о – внутри ∆


 А С А С п – в вершине прям. ∟ серединные
А С А С п – в вершине прям. ∟ серединные 
 В1 т – вне ∆, вне ∟
В1 т – вне ∆, вне ∟
1. ц.масс, центроид, 1. ц. впис. окр, 2. 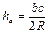 1. ц. опис. окружности
1. ц. опис. окружности
всегда внутри ∆ всегда внутри ∆ 3. 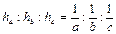 о – внутри ∆
о – внутри ∆
2. 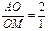 2.
2. 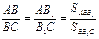 4.
4. 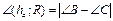 п – на середине гипот.
п – на середине гипот.
3. на 6 равновел. ∆ 3. между мед. и бис. т – вне ∆ , внутри угла
4. 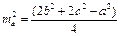 4.
4. 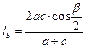
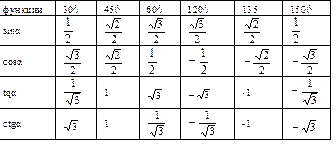
 5.
5. 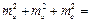 5.
5. 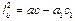
= 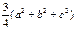

Вид ∆по сторонам
1. c2 = a2 + b2 – прямоугольный
2. с2 < а2 + b2 – остроугольный
3. с2 > а2 + b2 – тупоугольный,
где с – наибольшая


 Площадь треугольника
Площадь треугольника
1.S = 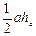
2. S = 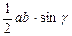
3. S = 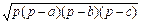 ,
,
где р = 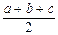
4. S = 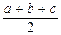 r
r
5. S = 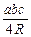
6. Sпрямоуг. = 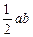 =
= 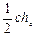

7. Sправ. = 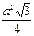

Средние линии

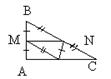
1. MN|| AC
2. MN = 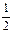 АС
АС  3. четыре равных ∆
3. четыре равных ∆
Признаки равенства
и подобия треугольников
1. по двум сторонам и
углу между ними
2. по стороне и двум углам
3. по трём сторонам
