Резонанс напряжений
Положим, что в цепи, содержащей последовательно соединенные емкость 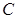 , индуктивность
, индуктивность 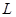 и обладающей активным сопротивлением
и обладающей активным сопротивлением 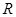 , действует переменная ЭДС, изменяющаяся по закону
, действует переменная ЭДС, изменяющаяся по закону
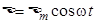 .
.
Тогда согласно сказанному в предыдущем разделе, в цепи будет протекать переменный ток
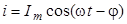 ,
,
амплитуда которого 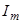 связана с амплитудой ЭДС
связана с амплитудой ЭДС 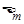 законом Ома для переменного тока
законом Ома для переменного тока
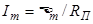 , (10)
, (10)
где 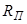 - есть сопротивление всей цепи:
- есть сопротивление всей цепи:
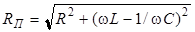 , (11)
, (11)
а фазовый угол 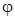 , на который колебания тока отстают от колебаний напряжения, определяется формулой (9).
, на который колебания тока отстают от колебаний напряжения, определяется формулой (9).
Допустим теперь, что мы изменяем частоту колебаний 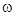 . Как показывают формулы (9)-(11), это вызовет изменение и амплитуды тока
. Как показывают формулы (9)-(11), это вызовет изменение и амплитуды тока 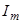 , и сдвига фазы
, и сдвига фазы 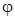 .
.
Остановимся сначала на изменениях амплитуды тока. Если 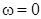 , то
, то 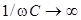 . Тогда сопротивление цепи
. Тогда сопротивление цепи 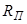 обращается в бесконечность и
обращается в бесконечность и 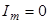 . Это и понятно, так как при
. Это и понятно, так как при 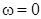 мы имеем постоянный ток, а постоянный ток не проходит через конденсатор. При увеличении
мы имеем постоянный ток, а постоянный ток не проходит через конденсатор. При увеличении 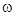 квадрат реактивного сопротивления
квадрат реактивного сопротивления 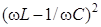 сначала уменьшается. Поэтому и сопротивление
сначала уменьшается. Поэтому и сопротивление 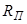 уменьшается, а
уменьшается, а 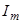 увеличивается. При частоте
увеличивается. При частоте 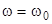 , определяемой условием
, определяемой условием
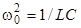 , (12)
, (12)
реактивное сопротивление 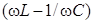 обращается в нуль, а сопротивление цепи становится наименьшим, равным активному сопротивлению цепи. Сила тока достигает при этом максимума. При
обращается в нуль, а сопротивление цепи становится наименьшим, равным активному сопротивлению цепи. Сила тока достигает при этом максимума. При 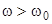 квадрат реактивного сопротивления снова не равен нулю и увеличивается с возрастанием
квадрат реактивного сопротивления снова не равен нулю и увеличивается с возрастанием 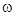 . В соответствии с этим сопротивление
. В соответствии с этим сопротивление 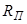 увеличивается, а амплитуда тока
увеличивается, а амплитуда тока 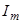 уменьшается, асимптотически приближаясь к нулю при увеличении
уменьшается, асимптотически приближаясь к нулю при увеличении 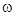 .
.
Зависимость 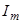 от
от 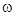 , выражаемая формулами (10), (11) приведена на рис.10, где показаны две кривые, соответствующие различным значениям активного сопротивления
, выражаемая формулами (10), (11) приведена на рис.10, где показаны две кривые, соответствующие различным значениям активного сопротивления 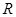 . Чем меньше
. Чем меньше 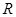 , тем выше и острее максимумы кривых.
, тем выше и острее максимумы кривых.
Обратимся теперь к к сдвигу фаз между током и ЭДС. Из (9) видно, что при очень малых частотах, когда 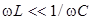 ,
, 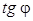 очень велик и отрицателен, и, следовательно,
очень велик и отрицателен, и, следовательно, 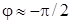 . В этом случае ток опережает напряжение и цепь имеет емкостной характер. При возрастании частоты
. В этом случае ток опережает напряжение и цепь имеет емкостной характер. При возрастании частоты  реактивное сопротивление
реактивное сопротивление 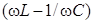 , оставаясь отрицательным, уменьшается по абсолютной величине и разность фаз
, оставаясь отрицательным, уменьшается по абсолютной величине и разность фаз 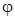 уменьшается. Когда
уменьшается. Когда 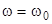 , формула (9) дает
, формула (9) дает 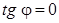 , а значит,
, а значит, 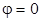 . При дальнейшем увеличении
. При дальнейшем увеличении 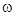 реактивное сопротивление становится положительным и увеличивается с возрастанием
реактивное сопротивление становится положительным и увеличивается с возрастанием 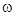 . Следовательно, при
. Следовательно, при 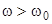 ток отстает от напряжения и цепь приобретает индуктивный характер, причем угол
ток отстает от напряжения и цепь приобретает индуктивный характер, причем угол 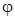 асимптотически стремится к предельному значению
асимптотически стремится к предельному значению 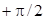 при увеличении частоты
при увеличении частоты 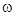 .
.
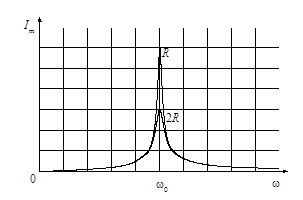 Рис.10. Амплитудно-частотная зависимость Рис.10. Амплитудно-частотная зависимость | 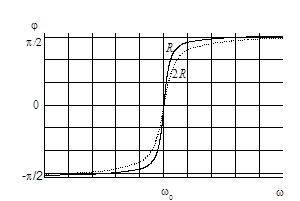 Рис.11. Фазово-частотная зависимость Рис.11. Фазово-частотная зависимость |
Зависимость сдвига фаз от частоты колебаний изображена графически на рис. 11. Также, как и 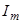 , фазовый сдвиг зависит от активного сопротивления контура
, фазовый сдвиг зависит от активного сопротивления контура 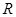 . Чем меньше
. Чем меньше 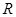 , тем быстрее изменяется
, тем быстрее изменяется 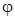 вблизи
вблизи 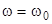 , и в предельном случае
, и в предельном случае  изменение фазы приобретает скачкообразный характер.
изменение фазы приобретает скачкообразный характер.
Резюмируя сказанное, мы видим, что особым является случай, когда частота ЭДС генератора (или приложенного внешнего напряжения) 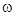 равна частоте
равна частоте 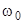 . При этом амплитуда тока достигает максимального значения, а сдвиг фаз между током и напряжением равен нулю, или иными словами, контур действует как чисто активное сопротивление. Этот важный случай вынужденных колебаний называется резонансом напряжений.
. При этом амплитуда тока достигает максимального значения, а сдвиг фаз между током и напряжением равен нулю, или иными словами, контур действует как чисто активное сопротивление. Этот важный случай вынужденных колебаний называется резонансом напряжений.
Отметим, что частота 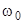 , при которой наступает резонанс равна частоте собственных колебаний контура без активного сопротивления (без затухания).
, при которой наступает резонанс равна частоте собственных колебаний контура без активного сопротивления (без затухания).
Найдем теперь, чему равны амплитуда колебаний напряжения на конденсаторе и фазовый сдвиг между этими колебаниями и колебаниями приложенного к контуру напряжения. Амплитуда напряжения на конденсаторе
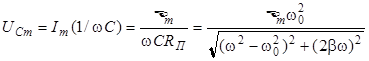 , (13)
, (13)
где 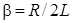 - коэффициент затухания контура. Фазовый сдвиг
- коэффициент затухания контура. Фазовый сдвиг 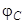 между колебаниями напряжения на конденсаторе и колебаниями приложенной ЭДС, как следует из рис.9, равен
между колебаниями напряжения на конденсаторе и колебаниями приложенной ЭДС, как следует из рис.9, равен
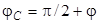 ,
, 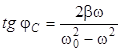 . (14)
. (14)
Основные качественные особенности зависимостей 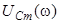 и
и 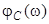 приведены в теоретической части описания лабораторной работы "Вынужденные колебания в последовательном колебательном контуре".
приведены в теоретической части описания лабораторной работы "Вынужденные колебания в последовательном колебательном контуре".
Рекомендуемая литература
1. С. Г. Калашников. Электричество. Москва, "Наука"-1985, § 217-223.
