ЗАВДАННЯ: параграф 13, №429, № 430, №436, №438
Урок № 51 – 52
Тема уроку.Теорема Піфагора. Розв’язування задач.
Перпендикуляр і похила, їх властивості.
Виконайте тест на визначення вірності математичних тверджень:
Якщо на запитання відповідь «так» ставимо «+», якщо «ні» ставимо «-».
Кожне завдання оцінюється в 1 бал.
Тест
1. Єгипетським називають прямокутник з катетами 3 і 4 та гіпотенузою 5.
2. Щоб знайти квадрат гіпотенузи, треба додати квадрати катетів.
3. Площа квадрата дорівнює a · b.
4. Якщо в прямокутному трикутнику катети дорівнюють 6 см і 8 см, то гіпотенуза дорівнює √ 28 см.
5. Гіпотенуза рівнобедреного прямокутного трикутника з катетом a дорівнює a√ 2 .
6. Діагональ квадрата зі стороною 2 см дорівнює 2 √2 см.
7. Діагональ прямокутника зі сторонами 13 см і 5 см дорівнює 12 см.
8. Периметр єгипетського трикутника дорівнює 12 см.
9. Радіус кола, описаного навколо прямокутного трикутника з катетами 6 см і 8 см, дорівнює 10 см.
10. Сторона ромба з діагоналями 6 см і 8 см дорівнює 5 см.
11. Катет прямокутного трикутника дорівнює 15 см, якщо його гіпотенуза дорівнює 25 см, а другий катет 20 см.
12. Медіана, проведена до гіпотенузи прямокутного трикутника з катетами 12 см і 5 см, дорівнює 13 см.
Питання класу
1. Які прямі називаються перпендикулярними?
2. Скільки прямих, перпендикулярних до даної, можна провести через точку на прямій? поза прямою?
3. Сформулюйте наслідок з теореми Піфагора.
Вивчення нового матеріалу
(записати в конспект)
Перпендикуляр і похила
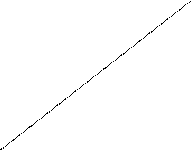

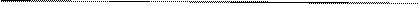 Нехай BA — перпендикуляр, опущений із точки B на пряму a, C∈а, C≠А . Відрізок BC називається похилою, проведеною із точки B до прямої a. Точка C називається основою похилої. Відрізок AC називається проекцією похилої.
Нехай BA — перпендикуляр, опущений із точки B на пряму a, C∈а, C≠А . Відрізок BC називається похилою, проведеною із точки B до прямої a. Точка C називається основою похилої. Відрізок AC називається проекцією похилої.
В
 |
С А а
Твердження 1. Якщо до прямої з однієї точки проведено перпендикуляр і похилу, то будь-яка похила більша від перпендикуляра.
Доведення
Це випливає з того, що в прямокутному трикутнику ABC катет BA менший від гіпотенузи BC.
Твердження 2. Із двох похилих, проведених з однієї точки до прямої, більшою є та, у якої проекція більша, і навпаки.
Доведення
Із трикутника CAB ∠А=90°: BC 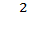 = AC
= AC 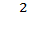 + АВ
+ АВ  Якщо сторона AB не змінюється, то видно, що чим більша сторона AC, тим більша BC, і навпаки, чим більша сторона BC, тим більша AC.
Якщо сторона AB не змінюється, то видно, що чим більша сторона AC, тим більша BC, і навпаки, чим більша сторона BC, тим більша AC.
Твердження 3Рівні похилі мають рівні проекції, і навпаки (якщо вони проведені з однієї точки до прямої).
В
 |
С А Д
1) трикутник CAB = трикутнику DAB, тому що вони прямокутні, у них BA — спільний катет і BC=BD. З рівності трикутників випливає, що AC=AD, і т. д.
2) Трикутник CBD — рівнобедрений, тому що BC= BD. Тоді AB — висота й медіана, тобтоAC=AD і т. д.
3) Можна сказати, що оскільки точка B є рівновіддаленою від кінців відрізка CD, то вона лежить на серединному перпендикулярі, тоді AC=AD.
4) з того, що AC =AD=, випливає рівність BC=BD.
Питання классу ( усно)
1. Що називається похилою?
2. Що називається проекцією похилої?
3. Сформулюйте властивість похилих.
ЗАВДАННЯ: параграф 13, №429, № 430, №436, №438
