Теорема косинусов

Теорема косинусов. Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

a2 = b 2 + c 2 – 2bc cosA

Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например,

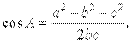
Расположение ортоцентров у треугольников различных типов Высоты треугольника (или их продолжения) пересекаются в одной точке.

Фигура	Рисунок	Описание
Остроугольный треугольник		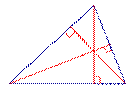Ортоцентр остроугольного треугольника лежит внутри треугольника.
Прямоугольный треугольник		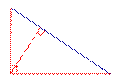Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Тупоугольный треугольник		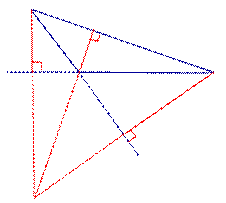Ортоцентр тупоугольного треугольника лежит вне треугольника. В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.

Биссектриса треугольника

Напомним, что биссектрисой угла называют луч, делящий угол пополам.

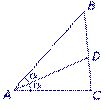
Определение. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).

Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.

На рисунке 1 биссектрисой является отрезок AD.

Теорема 1. Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

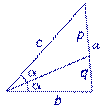
Следствие 1. Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения

Замечание. В любом треугольнике все три биссектрисы пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.