В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой

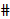1. Рассмотрим равнобедренный треугольник АВС с основанием ВС и биссектрисой AD.

BD = CD (по доказанному), следовательно, AD является так же и медианой.

Угол ADB = углу ADC = 90 градусов, поскольку они являются смежными, следовательно, AD является так же и высотой, .

6)Задачи на построение: серединного перпендикуляра к отрезку; биссектрисы угла; угла, равного данному.

1. Построение биссектрисы угла.

· Проведем окружность произвольного радиуса с центром в вершине угла.

· Проведем 2 окружности равного радиуса из этих точек, отметим точку пересечения окружностей, лежащую внутри угла.

· Из вершины угла через отмеченную точку проведем луч, который и будет являться биссектрисой угла.

2.Построение серединного перпендикуляра.

· Построим 2 окружности с центрами на концах отрезка и радиусами, равными этому отрезку.

· Соединим точки пересечения этих окружностей друг с другом и с концами отрезка.

· Используя радиусы, докажем, что образовавшиеся 2 треугольника равны и что прямая, соединяющая точки пересечения окружностей – серединный перпендикуляр.

3.Построение угла, равного данному.

· Построим произвольный луч.

· Построим окружность произвольного радиуса с центром в вершине данного угла, отметим точки пересечения ее со сторонами угла.

· Проведем окружность того же радиуса из начала построенного луча, отметим точку пересечения ее с лучом.

· Проведем окружность из точки пересечения окружности со стороной данного угла (радиус равен расстоянию между точками пересечения окружности со сторонами угла).

· Проведем окружность того же радиуса с центром в точке пересечения луча и окружности. Отметим точку пересечения этих окружностей.

· Проведем луч из отмеченной точки.

Параллельные прямые. Признаки параллельности прямых.

Параллельные прямые – 2 непересекающихся прямых в пространстве.

1.Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Доказательство через построение перпендикуляров и равенство треугольников.

2.Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Доказательство через вертикальные и накрест лежащие углы.

3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусов, то прямые параллельны. Доказательство через накрест лежащие углы.

Аксиомы геометрии.

1. Каждой прямой принадлежат по крайней мере две точки.

2. Имеются по крайней мере три точки, не лежащие на одной прямой.

3. Через любые две точки проходит прямая, и притом только одна.

4. Из трех точек прямой одна и только одна лежит между двумя другими.

5. Каждая точка О прямой делит ее на 2 луча так, что любые 2 точки одного и того же луча лежат по одну сторону от О, а любые 2 точки разных лучей лежат по разные стороны от точки О. При этом точка О не принадлежит ни одному из этих лучей.

6. Каждая прямая а делит плоскость на две части так, что любые 2 точки одной и той же полуплоскости лежат по одну сторону от а, а 2 точки разных полуплоскостей лучей лежат по разные стороны от а. При этом прямая а называется границей каждой из указанных полуплоскостей, ее точки не принадлежат ни одной из полуплоскостей.

7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.

8. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

9. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и при том только один.

10. Любой угол можно совместить с равным ему двумя способами.

11. Любая фигура равна самой себе.

12. Если первая фигура равна второй, тои вторая фигура равна первой.

13. Если первая фигура равна второй, а вторая – третьей, то первая фигура равна третьей.

14. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.

15. При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.

16. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Сумма углов треугольника.

Сумма градусных мер всех углов в любом треугольнике равна 180 градусам. Доказательство проводится с помощью проведения прямой, параллельной основанию, через вершину и нахождение равных углов.