Розклад вектора за базисом , , . Координати вектора
Візьмемо прямокутну декартову систему координат в просторі і разом з нею три одиничні вектори 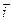 ,
, 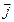 і
і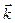 .Домовимося, що:
.Домовимося, що:
1) початок векторів 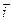 ,
, 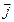 і
і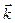 співпадає з початком аоординат;
співпадає з початком аоординат;
2) вектори 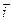 ,
, 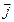 і
і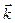 мають одинакові напрями з додатними напрямами осей координат Ox, Oy і Oz відповідно.
мають одинакові напрями з додатними напрямами осей координат Ox, Oy і Oz відповідно.
Означення 13.Сисатема векторів 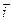 ,
, 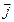 і
і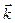 називається декартовим прямокутним базисом.
називається декартовим прямокутним базисом.
Теорема.Будь-який вектор 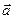 можна розкласти по базису
можна розкласти по базису 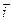 ,
, 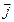 і
і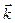 , тобто
, тобто
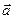 =ax
=ax 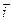 + ay
+ ay 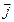 + az
+ az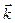 ,
,
де ax , ay і az – координати вектора 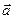 .
.
Операції над векторами, заданими координатами. Рівність і колінеарність двох векторів
1. Операції над векторами.Якщо відомі координати векторів, то операціям над векторами відповідають арифметичні операції над їхніми координатами.
Нехай задано вектори 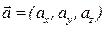 ,
, 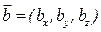 і дійсне число
і дійсне число 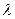 , тоді:
, тоді:
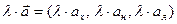 ,
, 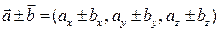 .
.
2. Рівність векторів. Нехай вектори 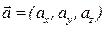 та
та 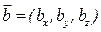 рівні, тобто мають однакові довжини і напрями, тоді мають місце рівності:
рівні, тобто мають однакові довжини і напрями, тоді мають місце рівності:
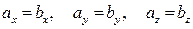 .
.
Справедливе і обернене твердження: якщо рівні координати двох векторів, то рівні і вектори.
3. Колінеарність двох векторів. Необхідною і достатньою умовою колінеарності двох векторів 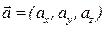 та
та 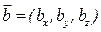 , є пропорціональність їхніх координат:
, є пропорціональність їхніх координат:
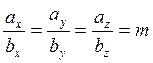 . (8)
. (8)
Справді, якщо вектори 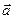 і
і 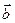 колінеарні, то має місце рівність
колінеарні, то має місце рівність 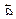 = m
= m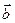 .Тоді з умови рівності двох векторів можемо записати рівності:
.Тоді з умови рівності двох векторів можемо записати рівності: 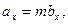
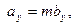
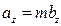 , з яких випливає формула (8).
, з яких випливає формула (8).
Скалярний добуток двох векторів
Означення 14.Скалярним добутком двох векторів 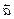 і
і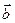 і позначається
і позначається 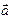 ·
· 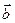 називають число, яке дорівнює добутку модулів цих векторів на косинус кута між ними, тобто
називають число, яке дорівнює добутку модулів цих векторів на косинус кута між ними, тобто
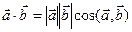 .
.
Якщо вектори перпендикулярні один до одного то скалярний добуток цих векторів дорівнює нулю, тобто
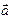 ·
· 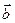 =0.
=0.
Якщо вектори задані своїми координатами, то скалярний добуток цих векторів обчислюється за формулою
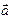 ·
· 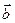 = ax bx + ayby +azbz
= ax bx + ayby +azbz
Довжина вектора, заданого координатами. Відстань між двома точками
Нехай вектор 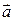 заданий своїми координатами:
заданий своїми координатами: 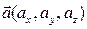 . Тоді довжина вектора або його модуль обчислюється за формулою
. Тоді довжина вектора або його модуль обчислюється за формулою
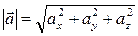
Нехай задано точки A(xa; ya; za) і B(xb; yb; zb). Тоді відстань між цими точками обчислюється за формулою:
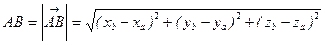
Кут між двома векторами
Знаючи правило обчислення скалярного добутку, можна знайти косинус кута між векторами
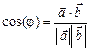 .
.
Якщо вектори задані своїми координатами: 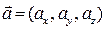 і
і 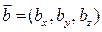 , тоді косинус кута між векторами обчислюється за формулою
, тоді косинус кута між векторами обчислюється за формулою
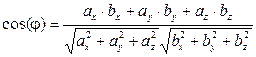 .
.
Приклад 3.Знайти кут між діагоналями паралелограма, побудованого на векторах 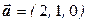 та
та 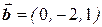 .
.
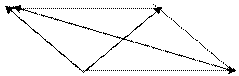
Розв’язання. За умовою задачі паралелограм побудовано на векторах 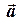 та
та 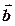 (див. рис. 18).
(див. рис. 18).
 D C
D C
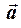
A 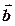 B
B
Рис.18
Позначимо цей паралелограм через ABCD ( 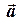 та
та 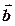 – довільні). Тоді
– довільні). Тоді
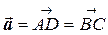 ;
; 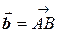 ;
; 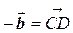 ;
; 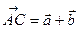 ;
; 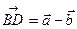 .
.
Отже, діагоналі паралелограма, побудованого на векторах 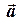 та
та 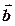 будуть вектори
будуть вектори 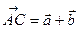 та
та 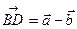 . Знайдемо координати цих векторів для заданих векторів
. Знайдемо координати цих векторів для заданих векторів 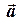 та
та 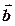 :
:
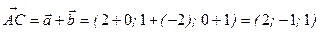 ,
,
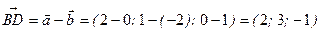 .
.
Тепер за формулою для косинуса кута між векторами можна знайти косинус потрібного кута, який позначимо через j
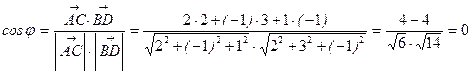 .
.
З рівності 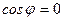 випливає, що
випливає, що 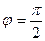 , тобто ці вектори взаємно перпендикулярні.
, тобто ці вектори взаємно перпендикулярні.
