Понятие многогранника и его элементы

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 20»

РЕФЕРАТ ПО ГЕОМЕТРИИ

В мире

Правильных

Многогранников

Ф.И.О. учащегося Белянкина Мария

Класс 11А

РуководительКозак Татьяна Ивановна,

учитель математики I категории

Пгт. Прогресс

Год

Содержание

	Введение	…………………
1.	Понятие многогранника и его элементы	…………………
	1.1 Виды многогранников	…………………
	1.2 Правильные многогранники	…………………
	1.3 Философ Платон и четыре стихии природы	…………………
	1.4 Тела Пуансо и архимедовы тела	…………………
2.	Многогранники в различных областях культуры и науки	…………………
	2.1 Многогранники в живописи	…………………
	2.2 Мнимая «Космографическая тайна» И.Кеплера	…………………
	2.3 Теория четырёх стихий мироздания	…………………
	2.4 Правильные многогранники в живой природе	…………………
3.	Изготовление правильных многогранников	…………………
	3.1 «Рождение» великого физика Д.К.Максвелла	…………………
	3.2 Развёртки правильных многогранников	…………………
	3.3 Способ «плетения»	…………………
	3.4 Ещё один способ изготовления многогранников	…………………
	3.4.1 Тетраэдр	…………………
	3.4.2 Октаэдр	…………………
	3.4.3 Гексаэдр (куб)	…………………
	3.4.4 Икосаэдр	…………………
	3.4.5 Додекаэдр	…………………
	Заключение	…………………
	Литература	…………………
	Приложение 1	…………………
	Приложение 2	…………………
	Приложение 3	…………………
	Приложение 4	…………………

Введение

С первых уроков геометрии в старших классах начинается взаимосвязанное изучение начал стереометрии и фигур в пространстве, в частности многогранников. Это объясняется тем, что многогранники являются хорошей иллюстрацией для вводимых понятий и доказательств, объяснения необходимости изучаемых свойств.

Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребёнка, играющего деревянными кубиками, до зрелого математика. Особый интерес к правильным многоугольникам и правильным многогранникам связан с красотой и совершенством формы. Они довольно часто встречаются в природе. Достаточно вспомнить форму снежинок, граней кристаллов, ячеек в пчелиных сотах. Из правильных многоугольников можно складывать не только плоские фигуры, но и пространственные. Многие из нас склеивали новогодние игрушки из открыток или яркой бумаги в форме правильных многогранников.

Многие строения в окружающем нас мире, в частности пирамида Хеопса, имеют форму многогранников. «Только неотступно следуя законам геометрии, архитекторы древности могли создать свои шедевры. Не слу­чайно говорят, что пирамида Хеопса – немой трактат по геометрии, а грече­ская архитектура – внешнее выраже­ние геометрии Евклида. Прошли века, но роль геометрии не изменилась. Она по-прежнему остается грамматикой ар­хитектора» – это высказывание принадлежит великому французскому архитектору нашего столетия Ле Корбюзье (1887–1965).

И самая популярная форма современного здания, радиоприемника, те­левизора, шкафа – параллелепипед; спичечный коробок, книга, комната, молочные пакеты также имеют форму тетраэдра или параллелепипеда. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. «Правильных многогранников вызывающе мало, – написал когда-то Л. Кэрролл – но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».

Правильных многоугольников на плоскости бесконечно много. А сколько существует правильных многогранников? Как они определяются? Как можно сделать правильный многогранник, например, из бумаги, возможно ли это, какими свойствами они обладают, где встречаются, имеют ли практическое применение? Поиском ответов на эти вопросы и является данная работа.

Итак,цельэтой работы:

¨ систематизация знаний и получение новой информации о многогранниках.

Задачи:

Ø изучить дополнительную литературу по теме;

Ø показать связь полученной информации с жизнью;

Ø описать технологию построения правильных многогранников.

Используемые методы:

¨ научный (изучение литературы);

¨ исследовательский.

Понятие многогранника и его элементы

Виды многогранников

Многогранники выделяются среди пространственных фигур как фигуры, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно рёбрами и вершинами многогранника. Примерами многогранников являются:

à параллелепипед – многогранник, поверхность которо­го состоит из шести параллелограммов;

à прямоугольный параллелепипед – параллелепипед, у которого грани –прямоугольники;

à куб – многогранник, поверхность которого состоит из шести квадратов;

à призма – многогранник, поверхность которого состоит из двух рав­ных многоугольников, называемых основаниями призмы, и параллелограммов, называемых боковыми гранями;

à прямая призма – призма, боковыми гранями которой являются прямоугольники;

à правильная призма – прямая призма, основаниями которой являются правильные многоугольники;

à пирамида – многогранник, поверхность которого со­стоит из многоугольника, называемого основанием пира­миды, и треугольников, имеющих общую вершину, назы­ваемых боковыми гранями пирамиды. Общая вершина треугольников называется вершиной пирамиды;

à правильная пирамида – пирамида, в основании кото­рой правильный многоугольник, и все боковые ребра рав­ны;

à усечённая пирамида – многогранник, гранями которого являются n-угольники (нижнее и верхнее основания), расположенные в параллельных плоскостях, и n-четырёхугольников (боковые грани).

Правильные многогранники

Среди разнообразных форм многогранников выде­ляют правильные многогранники – те, ко­торые построены из одинаковых многоуголь­ников, причем в каждой вершине сходится одинаковое количество таких многоугольни­ков.

Рассмотрим определения правильных многогранников, которые даются в разных учебниках, рекомендованных для общеобразовательных школ.

¨ В учебнике «Геометрия, 10-11 классы» (Л.С. Атанасян и др.) даётся такое определение правильного многогранника: «Выпуклый многогранник называется правильным, если все его грани – правильные многоугольники и в каждой его вершине сходится одно и то же число ребер». Такое же определение даётся и в учебниках А. В. Погорелова «Геометрия. Учебник для 7-11 классов средней школы» и И. М. Смирновой, В.А. Смирнова. «Геометрия. Учебник для 10-11 классов общеобразовательных учреждений».

¨ Многогранник называется правильным, если все его грани – равные правильные многоугольники, а все его вершины одинаково удалены от некоторой точки – центра правильного многоугольника (Г. П. Бевз, В. Г. Бевз, Н. Г. Владимирова. Геометрия 7-11 классы).

¨ Если все грани выпуклого многогранника – конгруэнтные правильные многоугольники и число рёбер, выходящих из каждой вершины, одинаково, то многогранник называется правильным (В. М. Клопский, З. А. Скопец, М. И. Ягодовский. Геометрия. Учебное пособие для 9-10 классов средней школы).

Но какое бы определение мы не взяли, главная суть заключается в следующем – все его грани равные правильные многоугольники. Во всех этих определениях можно увидеть свойства правильных многогранников: все плоские углы равны, все двугранные углы, содержащие две грани с общим ребром, равны, все рёбра равны, все многогранные углы равны, в каждой вершине сходится одно и то же число рёбер, все его вершины одинаково удалены от центра правильного многогранника. Примером правильного многогранника является куб. Все его грани – правильные квадраты, и к каждой вершине сходится три ребра.

Ещё в Древней Греции были описаны все правильные многогранники. Особенно важное место многогранникам уделяли пифагорейцы – ученики школы Пифагора (VI – V века до н. э.), где устройство мира тесно связывалось с геометрией, геометрическим телами. Именно им древнегреческий математик Прокл (V в.) приписывал построение пяти правильных многогранников, которые использовались для философ­ских космологических теорий. Согласно этим теориям элементы первоосновы бытия: огонь, земля, воздух, вода – имеют форму правильных многогранни­ков, соответственно правильного тет­раэдра, куба, октаэдра и икосаэдра. Но позже было установлено, что Пифагор мог знать, самое большее, гексаэдр (куб), тетраэдр и додекаэдр. В то время как октаэдр и икосаэдр были, вероятно, открыты лишь Теэтетом Афинским в IV в. до н. э.

Итак, существует всего пять правильных многогранников.

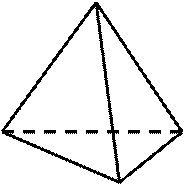Простейшим среди многогранников является тетраэдр (четырёхгранник – от греческого «тетра», т.е. четыре). Его четыре гра­ни – равносторонние треугольники. Четыре – это наименьшее число гра­ней, отделяющих часть трёхмерного пространства. Тем не менее, тетраэдр обладает многими свойствами, харак­терными для однородных многогран­ников. Все его грани суть правильные многоугольники, причём каждая отде­ляется ребром в точности от одной грани. Все многогранные углы тетра­эдра также равны между собой.

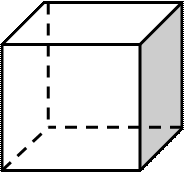Куб, или гексаэдр(шестигранник – от греческого «гекса», т.е. шесть) – са­мый общеизвестный и широко исполь­зуемый многогранник. Все шесть его граней – квадраты, сходящиеся по два вдоль каждого ребра и по три в каж­дой вершине.

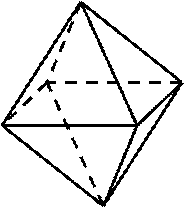
Октаэдр (восьмигранник – от греческого «окта», т.е. восемь), составлен­ный из восьми правильных треугольников, его противоположные грани лежат в параллельных плоскостях. Иоганн Кеплер (1571-1630) в своём этюде «О снежинке» высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных – куб, а его, если позволительно так сказать, супруга – октаэдр, ибо у октаэдра столько углов, сколько у куба граней».

Икосаэдр (двадцатигранник – от греческого «икос», т.е. двадцать), составленный из двадцати правильных треугольников. Икосаэдр – одно из пяти тел, по простоте следующее за тетраэдром и октаэдром. Их объединя­ет то обстоятельство, что гранями 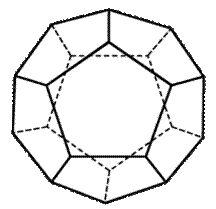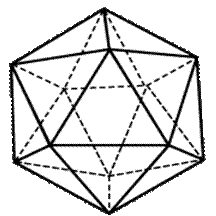каждого являются равносторонние тре­угольники.

И за­гадочный додекаэдр (двенадцатигранник – от греческого «додека», т.е. двенадцать), со­ставленный из двенадцати правильных пя­тиугольников. В известном смысле додекаэдрпред­ставляет наибольшую привлекатель­ность среди тел, соперни­чая с икосаэдром, который почти ему не уступает (а быть может, в чём-то и превосходит).