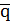Описание ЭВМ на уровне операционных схем и микропрограмм

На этом уровне ЭВМ можно рассматривать как совокупность операционных устройств, каждое из которых предназначено для выполнения определенного набора операций F={f₁, f₂, …, f_S}. Операции производятся над множеством входных слов A={a₁, a₂, …, a_q} и множеством внутренних (промежуточных) слов R={r₁, r₂, …, r_p}. Результатом выполнения операций является множество выходных слов C={c₁, c₂, …, с_k}, то есть с_i = f_j (A U R). Операционное устройство (ОУ) можно представить в виде «черного ящика» следующим образом (рис.1.2).

ОУ

A

C

F

Рис.1.2

Математик Глушков В.М. предложил любое операционное устройство рассматривать в виде композиции двух автоматов: операционного автомата (ОА) и управляющего автомата (УА) (рис.1.3), где: X={x₁, x₂, …, x_n} – множество логических условий, Y={y₁, y₂, …, y_m} – множество микроопераций.

OA

УA

A

X

Y

C

F

Рис.1.3

Любая операция из множества F может быть реализована последовательностью элементарных операций называемых микрооперациями.

Микрооперация – это элементарное машинное действие, которое не может быть разбито на более простые составляющие и которое выполняется за один машинный такт.

Микрокоманда – это совокупность микроопераций, выполняемых одновременно в одном машинном такте, при выполнении микропрограммы.

Микропрограмма – это алгоритм выполнения машинной операции, описанный в терминах микроопераций и логических условий

УА предназначен для реализации микропрограммы, т.е. для формирования последовательности управляющих сигналов y_i, которые инициализируют выполнение одноименных микроопераций в ОА.

ОА предназначен для хранения слов информации (множества A, R, C), выполнения микроопераций над этими словами и формирования значений логических условий x_i.

ОА состоит из совокупности операционных элементов (ОЭ), которые объединяются в единую схему с помощью шин, используемых для передачи слов информации и электрических цепей для передачи двоичных сигналов управления. Шина является совокупностью электрически независимых цепей.

Операционные элементы

Каждый из операционных элементов ОЭ описывается :

1) хранимым или вычисляемым словом информации;

2) множеством реализуемых микроопераций;

3) множеством формируемых логических условий.

Основные типы операционных элементов

1. Управляемая шина для реализации микрооперации передачи слова информации. Условное обозначение управляемой шины и ее реализация из логических элементов изображены на рис.1.4. На условном изображении шина изображена в виде широкой стрелки, а цепь управления в виде тонкой стрелки.

C(k)

yi

A(k)

C(k) = A(k) , если yi = 1

&

&

c1

ck

yi

a1

a k

. . .

Рис.1.4

2. Регистр для реализации микрооперации передачи и хранения слова информации. Регистр – это линейка триггеров, каждый из которых хранит один бит информации (0,1). На условном обозначении регистра (рис.1.5) микрооперация y_i производит запись слова A длиной k разрядов в регистр. Значение первого разряда регистра определяет значение логического условия x_j

RG

yi (запись)

xj

C

A

k

Рис.1.5

3. Сдвигающий регистр служит для хранения слова информации и выполнения микрооперации сдвига над этим словом. На рис.1.6. представлен реверсивный регистр так как по микрооперации y_p происходит сдвиг содержимого регистра на 1 разряд влево, а по микрооперации y_s - сдвиг содержимого на 1 разряд вправо. Запись в регистр происходит по сигналу y_f.

RG

yp

xj

C

k

A

ys

yf

Рис.1.6

4. Счетчик предназначен для хранения слова информации и выполнения над ним микрооперации счета, которая состоит в изменении значения слова (состояния счетчика) на единицу. Счетчик, в котором реализуется микрооперация вида С=С+1 называется суммирующим, а счетчик, реализующий микрооперацию С=С-1 называется вычитающим. Счетчик, в котором реализуются обе микрооперации, называется реверсивным. Двоичный k – разрядный счетчик может находиться в 2^k состояний. Значение 2^k -1 – это максимальное значение, которое может содержать такой счетчик и называемое ёмкостью счетчика (рис.1.7).

СT

yd

xj

C

k

A

yo

yp

ya

Рис.1.7

Микрооперации: Логическое условие:

1, если СT = 0;   0, если СT ≠ 0.

y_o – обнуление СT : = 0;

y_p –запись кода CT := 2^k -1; x_{j =}

y_a – прямой счет CT := CT + 1;

y_d – обратный счет CT := CT - 1.

5. Комбинационные схемы, реализующие системы булевых функций. Примером использования типовых комбинационных схем в качестве операционных элементов являются дешифратор и комбинационный сумматор. Дешифратор предназначен для преобразования k-разрядного двоичного кода в n – разрядный двоичный унитарный код, т.е. в код содержащий одну единицу.

На рис.1.8. условное обозначение дешифратора на k входов, n выходов и таблица истинности, задающая полный дешифратор на 2 входа.

DC

C

A

n

k

k=2 n=4 a1 a2 c1 c2 c3 c4

Рис.1.8

6. Комбинационный сумматор - это операционный элемент, предназначенный для выполнения микрооперации сложения чисел типа C= A + B (рис.1.9).

C = c1 c2 . . . cn; A = a1 a2 . . . an; B = b1 b2 . . . bn.   p – вход переноса, q – выход переноса

SM

A

n

p

q

B

C

Рис.1.9

Комбинационный сумматор состоит из линейки одноразрядных сумматоров последовательно соединенных цепью переноса из младшего разряда сумматора в старший (рис.1.10).

p1 q2

q1

c1

a1

b1

SM1

SM2

SMn

c2

cn

b2

bn

a2

an

p2

qn

pn

. . .

Рис.1.10

Сложение чисел A и B сводится к поразрядному сложению одноименных разрядов слагаемых, т.е. q_i c_i = a_i + b_i + p_i , i = 1, 2 . . .n, где:

q_i c_i – двухразрядное двоичное число;

q_i – значение переноса, которое вырабатывается в разряде i и переносится в разряд i – 1;

c_i – разряд суммы;

a_i и b_i – одноименные разряды слагаемых;

p_i – перенос из предыдущего младшего разряда т.е. p_i = q _{i + 1} , p_n = 0.

p

q

c

a

b

SM

a b p q c

Рис.1.11

Один разряд комбинационного сумматора можно рассматривать как комбинационную схему с двумя выходами: q, c и тремя входами: a, b, p.

Исходя из правил выполнения двоичного сложения двух целых двоичных чисел, составим таблицу истинности для системы из двух булевых функций q, c, зависящих от трех переменных a, b, p (рис.1.11).

b p

c

q

b p

a

a

Рис.1.12

Каждой функции q и c соответствуют карты Карно (рис.1.12). После минимизации соответствующих булевых функций, получаются следующие их минимальные дизъюнктивные формы:

q= a p ˅ a b ˅ b p;

c= a ˅ p ˅ a b p ˅ b .

Используя аксиомы и теоремы булевой алгебры можно представить последнею функцию в следующем виде:

c= (a ˅ b ˅ p) ˅ a b p, где: – инверсия q.

На рис.1.13 представлена схема, реализующая эти функции в булевом базисе и являющаяся схемой одного разряда комбинационного сумматора.

a b p

&

&

abp

ap

ab

c

&

bp

&

&

a ˅ b ˅ p

q

Рис.1.13

Накапливающий сумматор - это операционный элемент, предназначенный для выполнения микрооперации сложения чисел типа C=C + A и состоит из регистра и комбинационного сумматора (рис.1.14.).

n

n

RG

SM

C

A

y1-запись

y0- сброс

n

SM

C

y0

y1

A

Рис.1.14

Для описания микропрограмм используются следующие языки:

- язык графической схемы алгоритма (ГСА);

- язык логических схем алгоритма (ЛСА);

- язык матричных схем алгоритма (МСА).

Язык графической схемы алгоритма - это ориентированный граф с вершинами следующих типов:

– начальная операторная вершина, помеченная символом начальной микрооперации y0;

У0

– конечнaя операторная вершина, помеченная символом конечной микрооперации yк ;

Ук

yi

– условная вершина, помеченная символом логического условия xj;

xj

– операторная вершина, помеченная символом микрооперации yi или микрокомандой;

Условия корректности ГСА:

- должен существовать путь из начальной вершины в любую другую операторную вершину, т.е. любая вершина должна быть достижима;

- должен существовать путь из любой операторной вершины в конечную вершину, т.е. не должно быть тупиковых вершин.

Достоинством ГСА является их наглядность, а недостатком – громоздкость.

На рис.1.15 приведен пример линейной ГСА, на рис 1.16 – разветвляющейся ГСА, на рис 1.17 – циклической ГСА.

y0

yk

y2

y3

x1

x2

y4

y1

y0 У0

y1

. . . .

y k-1

yk

Рис.1.15 Рис.1.16

y0

y1

x1

y2

y3

x2

yk

Рис.1.17

Язык логических схем алгоритма – это строчная запись операторов алгоритма.

Операторы используются следующих типов:

Y₀ - начальный оператор;

Y_k - конечный оператор;

Y_i - исполняемый оператор;

Х_j - оператор логического условия, который снабжается открывающей и закрывающей полускобкой с индексом, определяющим соответствие между этими полускобками;

[_k - открывающая полускобка;

_k] - закрывающая полускобка.

Оператор логического условия выполняется следующим образом:

если Х_j = 1, то следующим выполняется оператор стоящий после открывающей полускобки , если Х_j = 0, то следующим выполняется оператор стоящий после соответствующей закрывающей полускобки.

Х_j [_{k . . .k}]

Для задания безусловного перехода используется тождественно ложный логический оператор:

O_j [_{m . . .m}]

Запись линейного алгоритма (рис.1.15) на языке ЛСА имеет следующий вид:

Y₀ Y_{1 . . .} Y_к-1Y_к.

Запись разветвляющегося алгоритма (рис.1.16) на языке ЛСА имеет вид:

Y₀ Y₁ X₁ [₂ X₂ [₃ Y₄ O₁ [_{4 3}] Y₃ O₂ [_{5 2}] Y_{2 5}] ₄] Y_к.

Запись циклического алгоритма (рис.1.17) на языке ЛСА имеет вид:

Y_{0 1}] Y₁ X₁ [₂ Y₃ O₁ [_{3. 2}] Y_{2 3}] X₂ [₁ Y_к.

Условия корректности ЛСА: баланс открывающих и закрывающих скобок.

Достоинством ЛСА является компактность, а недостатком - отсутствие наглядности.

Язык матричных схем алгоритма - это квадратная матрица, строки которой отмечены индексами операторов от 0 до k – 1, а столбцы индексами от 1 до k. На пересечении i – той строки и j – того столбца записывается условие достижения j – того оператора из i – того оператора.

Запись линейного алгоритма (рис.1.15) на языке МСА представлена в табл. 1.1.

Таблица 1.1

	y1	y2	. . .	yk
y0
y1
.
yk-1

Начальная вершина микропрограммы помечена микрооперацией y0. Безусловный переход из вершины, помеченной микрооперацией у0 в вершину, помеченную микрооперацией y1 определяется значением единицы в соответствующей клетке матрицы.

Запись разветвляющегося (рис.1.16) и циклического алгоритма (рис.1.17) представлены на языке МСА в табл. 1.2 и в табл. 1.3 соответственно.

Таблица 1.2 Таблица 1.3

	y1	y2	y3	y4	yk
y0
y1		x1	x1 x2	x1 x2
y2
y3
y4

	y1	y2	y3	yk
y0
y1		x1	x1
y2	x2			x2
y3	x2			x2

Условия корректности МСА:

- отсутствие пустых строк и столбцов;

- в каждой строке значение дизъюнкции конъюнкций логических условий, записанных в клетках этой строки, должна быть тождественно равно единице.

Эти два условия одновременно проверяют достижимость операторных вершин и отсутствие тупиковых вершин.

Достоинство: удобство хранения в памяти компьютера и возможность использования аппарата матричной алгебры.

Недостаток: громоздкость при большом количестве операторов и отсутствие наглядности.