Введение в микропрограммное управление и теорию конечных автоматов
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
Учреждение ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНия
В.С.Дудкин
ТЕОРИЯ АВТОМАТОВ
Учебное пособие для студентов очной формы обучения
Санкт-Петербург
ВВЕДЕНИЕ В МИКРОПРОГРАММНОЕ УПРАВЛЕНИЕ И ТЕОРИЮ КОНЕЧНЫХ АВТОМАТОВ
Уровни представления ЭВМ
Электронная вычислительная машина (ЭВМ) - это комплекс электронного оборудования, выполняющий интерпретацию машинных программ, предназначенных для преобразования информации представленной в цифровой форме.
Сложность функционирования и иерархический характер организации машины определяют пять различных уровней представления и описания ЭВМ.
1. Уровень электрических схем. Электрическая схема - это совокупность взаимосвязанных электрических элементов: диодов, транзисторов, сопротивлений и емкостей. Этот уровень отражает физические процессы, происходящие в ЭВМ. Описание этих схем используется для изготовления и отладки ЭВМ.
2. Уровень логических схем. На этом уровне ЭВМ – сеть из логических элементов и ее функционирование рассматривается как выполнение логических операций над битами информации.
3. Уровень операционных схем и микропрограмм. ЭВМ детализируется до операционных элементов (счетчики, регистры, сумматоры) и управляющих устройств, реализующих микропрограммы.
4. Уровень структурных схем. ЭВМ рассматривается как совокупность взаимосвязанных структурных устройств: оперативная память, процессор, центральное устройство управления, устройства ввода и вывода (рис. 1.1).
5. Уровень машинных программ. Это уровень пользователя ЭВМ.
| Процессор |
| Устройство вывода |
| Устройство ввода |
| Память |
| Центральное устройство управления |
Рис. 1.1
Описание ЭВМ на уровне операционных схем и микропрограмм
На этом уровне ЭВМ можно рассматривать как совокупность операционных устройств, каждое из которых предназначено для выполнения определенного набора операций F={f1, f2, …, fS}. Операции производятся над множеством входных слов A={a1, a2, …, aq} и множеством внутренних (промежуточных) слов R={r1, r2, …, rp}. Результатом выполнения операций является множество выходных слов C={c1, c2, …, сk}, то есть сi = fj (A U R). Операционное устройство (ОУ) можно представить в виде «черного ящика» следующим образом (рис.1.2).
| ОУ |
| A |
| C |
| F |
Рис.1.2
Математик Глушков В.М. предложил любое операционное устройство рассматривать в виде композиции двух автоматов: операционного автомата (ОА) и управляющего автомата (УА) (рис.1.3), где: X={x1, x2, …, xn} – множество логических условий, Y={y1, y2, …, ym} – множество микроопераций.
| OA |
| УA |
| A |
| X |
| Y |
| C |
| F |
Рис.1.3
Любая операция из множества F может быть реализована последовательностью элементарных операций называемых микрооперациями.
Микрооперация – это элементарное машинное действие, которое не может быть разбито на более простые составляющие и которое выполняется за один машинный такт.
Микрокоманда – это совокупность микроопераций, выполняемых одновременно в одном машинном такте, при выполнении микропрограммы.
Микропрограмма – это алгоритм выполнения машинной операции, описанный в терминах микроопераций и логических условий
УА предназначен для реализации микропрограммы, т.е. для формирования последовательности управляющих сигналов yi, которые инициализируют выполнение одноименных микроопераций в ОА.
ОА предназначен для хранения слов информации (множества A, R, C), выполнения микроопераций над этими словами и формирования значений логических условий xi.
ОА состоит из совокупности операционных элементов (ОЭ), которые объединяются в единую схему с помощью шин, используемых для передачи слов информации и электрических цепей для передачи двоичных сигналов управления. Шина является совокупностью электрически независимых цепей.
Операционные элементы
Каждый из операционных элементов ОЭ описывается :
1) хранимым или вычисляемым словом информации;
2) множеством реализуемых микроопераций;
3) множеством формируемых логических условий.
Основные типы операционных элементов
1. Управляемая шина для реализации микрооперации передачи слова информации. Условное обозначение управляемой шины и ее реализация из логических элементов изображены на рис.1.4. На условном изображении шина изображена в виде широкой стрелки, а цепь управления в виде тонкой стрелки.
| C(k) |
| yi |
| A(k) |
| C(k) = A(k) , если yi = 1 |
| & |
| & |
| c1 |
| ck |
| yi |
| a1 |
| a k |
| . . . |
Рис.1.4
2. Регистр для реализации микрооперации передачи и хранения слова информации. Регистр – это линейка триггеров, каждый из которых хранит один бит информации (0,1). На условном обозначении регистра (рис.1.5) микрооперация yi производит запись слова A длиной k разрядов в регистр. Значение первого разряда регистра определяет значение логического условия xj
| RG |
| yi (запись) |
| xj |
| C |
| A |
| k |
Рис.1.5
3. Сдвигающий регистр служит для хранения слова информации и выполнения микрооперации сдвига над этим словом. На рис.1.6. представлен реверсивный регистр так как по микрооперации yp происходит сдвиг содержимого регистра на 1 разряд влево, а по микрооперации ys - сдвиг содержимого на 1 разряд вправо. Запись в регистр происходит по сигналу yf.
| RG |
| yp |
| xj |
| C |
| k |
| A |
| ys |
| yf |
Рис.1.6
4. Счетчик предназначен для хранения слова информации и выполнения над ним микрооперации счета, которая состоит в изменении значения слова (состояния счетчика) на единицу. Счетчик, в котором реализуется микрооперация вида С=С+1 называется суммирующим, а счетчик, реализующий микрооперацию С=С-1 называется вычитающим. Счетчик, в котором реализуются обе микрооперации, называется реверсивным. Двоичный k – разрядный счетчик может находиться в 2k состояний. Значение 2k -1 – это максимальное значение, которое может содержать такой счетчик и называемое ёмкостью счетчика (рис.1.7).
| СT |
| yd |
| xj |
| C |
| k |
| A |
| yo |
| yp |
| ya |
Рис.1.7
Микрооперации: Логическое условие:
| 1, если СT = 0; 0, если СT ≠ 0. |
yp –запись кода CT := 2k -1; xj =
ya – прямой счет CT := CT + 1;
yd – обратный счет CT := CT - 1.
5. Комбинационные схемы, реализующие системы булевых функций. Примером использования типовых комбинационных схем в качестве операционных элементов являются дешифратор и комбинационный сумматор. Дешифратор предназначен для преобразования k-разрядного двоичного кода в n – разрядный двоичный унитарный код, т.е. в код содержащий одну единицу.
На рис.1.8. условное обозначение дешифратора на k входов, n выходов и таблица истинности, задающая полный дешифратор на 2 входа.
| DC |
| C |
| A |
| n |
| k |
|
Рис.1.8
6. Комбинационный сумматор - это операционный элемент, предназначенный для выполнения микрооперации сложения чисел типа C= A + B (рис.1.9).
| C = c1 c2 . . . cn; A = a1 a2 . . . an; B = b1 b2 . . . bn. p – вход переноса, q – выход переноса |
| SM |
| A |
| n |
| p |
| q |
| B |
| C |
Рис.1.9
Комбинационный сумматор состоит из линейки одноразрядных сумматоров последовательно соединенных цепью переноса из младшего разряда сумматора в старший (рис.1.10).
| p1 q2 |
| q1 |
| c1 |
| a1 |
| b1 |
| SM1 |
| SM2 |
| SMn |
| c2 |
| cn |
| b2 |
| bn |
| a2 |
| an |
| p2 |
| qn |
| pn |
| . . . |
Рис.1.10
Сложение чисел A и B сводится к поразрядному сложению одноименных разрядов слагаемых, т.е. qi ci = ai + bi + pi , i = 1, 2 . . .n, где:
qi ci – двухразрядное двоичное число;
qi – значение переноса, которое вырабатывается в разряде i и переносится в разряд i – 1;
ci – разряд суммы;
ai и bi – одноименные разряды слагаемых;
pi – перенос из предыдущего младшего разряда т.е. pi = q i + 1 , pn = 0.
| p |
| q |
| c |
| a |
| b |
| SM |
|
Рис.1.11
Один разряд комбинационного сумматора можно рассматривать как комбинационную схему с двумя выходами: q, c и тремя входами: a, b, p.
Исходя из правил выполнения двоичного сложения двух целых двоичных чисел, составим таблицу истинности для системы из двух булевых функций q, c, зависящих от трех переменных a, b, p (рис.1.11).
| b p |
| c |
| q |
| b p |
| a |
| a |
Рис.1.12
Каждой функции q и c соответствуют карты Карно (рис.1.12). После минимизации соответствующих булевых функций, получаются следующие их минимальные дизъюнктивные формы:
q= a p ˅ a b ˅ b p;
c= a 
 ˅
˅ 
 p ˅ a b p ˅
p ˅ a b p ˅  b
b  .
.
Используя аксиомы и теоремы булевой алгебры можно представить последнею функцию в следующем виде:
c=  (a ˅ b ˅ p) ˅ a b p, где:
(a ˅ b ˅ p) ˅ a b p, где:  – инверсия q.
– инверсия q.
На рис.1.13 представлена схема, реализующая эти функции в булевом базисе и являющаяся схемой одного разряда комбинационного сумматора.
| a b p |
| & |
| & |
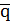 |
| abp |
| ap |
| ab |
| c |
| & |
| bp |
| & |
| & |
| a ˅ b ˅ p |
| q |
Рис.1.13
Накапливающий сумматор - это операционный элемент, предназначенный для выполнения микрооперации сложения чисел типа C=C + A и состоит из регистра и комбинационного сумматора (рис.1.14.).
| n |
| n |
| RG |
| SM |
| C |
| A |
| y1-запись |
| y0- сброс |
| n |
| SM |
| C |
| y0 |
| y1 |
| A |
Рис.1.14
Для описания микропрограмм используются следующие языки:
- язык графической схемы алгоритма (ГСА);
- язык логических схем алгоритма (ЛСА);
- язык матричных схем алгоритма (МСА).
Язык графической схемы алгоритма - это ориентированный граф с вершинами следующих типов:
| – начальная операторная вершина, помеченная символом начальной микрооперации y0; |
| У0 |
| – конечнaя операторная вершина, помеченная символом конечной микрооперации yк ; |
| Ук |
| yi |
| – условная вершина, помеченная символом логического условия xj; |
| xj |
| – операторная вершина, помеченная символом микрооперации yi или микрокомандой; |
Условия корректности ГСА:
- должен существовать путь из начальной вершины в любую другую операторную вершину, т.е. любая вершина должна быть достижима;
- должен существовать путь из любой операторной вершины в конечную вершину, т.е. не должно быть тупиковых вершин.
Достоинством ГСА является их наглядность, а недостатком – громоздкость.
На рис.1.15 приведен пример линейной ГСА, на рис 1.16 – разветвляющейся ГСА, на рис 1.17 – циклической ГСА.
| y0 |
| yk |
| y2 |
| y3 |
| x1 |
| x2 |
| y4 |
| y1 |
| y0 У0 |
| y1 |
| . . . . |
| y k-1 |
| yk |
Рис.1.15 Рис.1.16
| y0 |
| y1 |
| x1 |
| y2 |
| y3 |
| x2 |
| yk |
Рис.1.17
Язык логических схем алгоритма – это строчная запись операторов алгоритма.
Операторы используются следующих типов:
Y0 - начальный оператор;
Yk - конечный оператор;
Yi - исполняемый оператор;
Хj - оператор логического условия, который снабжается открывающей и закрывающей полускобкой с индексом, определяющим соответствие между этими полускобками;
[k - открывающая полускобка;
k] - закрывающая полускобка.
Оператор логического условия выполняется следующим образом:
если Хj = 1, то следующим выполняется оператор стоящий после открывающей полускобки , если Хj = 0, то следующим выполняется оператор стоящий после соответствующей закрывающей полускобки.
Хj [k . . .k]
Для задания безусловного перехода используется тождественно ложный логический оператор:
Oj [m . . .m]
Запись линейного алгоритма (рис.1.15) на языке ЛСА имеет следующий вид:
Y0 Y1 . . . Yк-1Yк.
Запись разветвляющегося алгоритма (рис.1.16) на языке ЛСА имеет вид:
Y0 Y1 X1 [2 X2 [3 Y4 O1 [4 3] Y3 O2 [5 2] Y2 5] 4] Yк.
Запись циклического алгоритма (рис.1.17) на языке ЛСА имеет вид:
Y0 1] Y1 X1 [2 Y3 O1 [3. 2] Y2 3] X2 [1 Yк.
Условия корректности ЛСА: баланс открывающих и закрывающих скобок.
Достоинством ЛСА является компактность, а недостатком - отсутствие наглядности.
Язык матричных схем алгоритма - это квадратная матрица, строки которой отмечены индексами операторов от 0 до k – 1, а столбцы индексами от 1 до k. На пересечении i – той строки и j – того столбца записывается условие достижения j – того оператора из i – того оператора.
Запись линейного алгоритма (рис.1.15) на языке МСА представлена в табл. 1.1.
Таблица 1.1
| y1 | y2 | . . . | yk | |
| y0 | ||||
| y1 | ||||
| . | ||||
| yk-1 |
| Начальная вершина микропрограммы помечена микрооперацией y0. Безусловный переход из вершины, помеченной микрооперацией у0 в вершину, помеченную микрооперацией y1 определяется значением единицы в соответствующей клетке матрицы. |
Запись разветвляющегося (рис.1.16) и циклического алгоритма (рис.1.17) представлены на языке МСА в табл. 1.2 и в табл. 1.3 соответственно.
Таблица 1.2 Таблица 1.3
| y1 | y2 | y3 | y4 | yk | |
| y0 | |||||
| y1 | x1 | x1 x2 | x1 x2 | ||
| y2 | |||||
| y3 | |||||
| y4 |
| y1 | y2 | y3 | yk | |
| y0 | ||||
| y1 | x1 | x1 | ||
| y2 | x2 | x2 | ||
| y3 | x2 | x2 |
Условия корректности МСА:
- отсутствие пустых строк и столбцов;
- в каждой строке значение дизъюнкции конъюнкций логических условий, записанных в клетках этой строки, должна быть тождественно равно единице.
Эти два условия одновременно проверяют достижимость операторных вершин и отсутствие тупиковых вершин.
Достоинство: удобство хранения в памяти компьютера и возможность использования аппарата матричной алгебры.
Недостаток: громоздкость при большом количестве операторов и отсутствие наглядности.
КОНЕЧНЫЕ АВТОМАТЫ
Введение
Все цифровые устройства можно разделить на два класса:
1. логические схемы;
2. схемы с памятью.
Логические и комбинационные схемы формируют значения выходных сигналов в зависимости от значений входных сигналов, подаваемых в данный момент независимо от значений входных сигналов, подаваемых на входы ранее. Для описания этих схем используются переключательные (булевы) функции.
В другом классе схем значение выходных сигналов зависят не только от значений входных сигналов, поступающих в данный момент, но еще и от значений сигналов, подаваемых на эти входы ранее, т.е. эти схемы учитывают предысторию входных сигналов. Эти схемы называются схемами с памятью или последовательностными схемами, так как они последовательность входных сигналов перерабатывают в последовательность выходных сигналов.
Для описания таких схем используется теория конечных автоматов.
Теория конечных автоматов
Основные определения:
1. конечная совокупность различных символов называется алфавитом;
2. каждый отдельный символ алфавита - буквой;
3. последовательность букв, имеющая конечную длину - словом;
4. число букв в слове - длиной;
5. два алфавита называются равнозначными, если между буквами этих алфавитов можно установить взаимно-однозначное соответствие.
Пример конечного автомата:
Пусть: P = {p1, p2, p3} – входной алфавит, W = {w1, w2} – выходной алфавит.
Будем рассматривать абстрактный конечный автомат в виде «черного ящика» с одним входом и одним выходом (рис. 2.1), т.е. анализируемое устройство описывается на уровне задания зависимости значений на его выходе от значений на его входе.
| t3 t2 t1 t0 p2 p3 p1 p3 p2 p1 p3 p3 |
| t3 t2 t1 t0 w2 w2 w1 w2 |
| A |
Рис. 2.1
Работа автомата рассматривается в дискретные моменты времени ti называемые автоматными тактами (i меняется от 0 до n, где n – длина входного слова). В примере на рис.2.1 в начальный момент времени t0 автомат входную букву р3 перерабатывает в выходную букву w2. В результате работы автомат входное слово p3p1p3p2 перерабатывает в выходное слово w2w1w2w2.
В общем случае конечный автомат определяет устройство, которое реализует отображение множества слов входного алфавита во множество слов выходного алфавита.
Различают два класса абстрактных автоматов:
1. автомат без выходного преобразователя;
2. автомат с выходным преобразователем.
АСИНХРОННЫЙ АВТОМАТ
Асинхронным автоматом называется автомат, изменение состояния которого может происходить в произвольный момент времени, и этот моменты времени определяются изменением входного сигнала.
Выбор способа реализации автомата (синхронный или асинхронный) определяется способом представления входного сигнала.
Примеры основных способов представления входных сигналов:
1. потенциальный с синхронизацией;
| t |
| t |
| c |
| x1 |
| t |
| t |
| V |
| c |
| x1 |
2. импульсный сигнал;
| x2 |
| t |
| V |
3. потенциальный сигнал.
| x3 |
| t |
| V |
При потенциальном сигнале высокий уровень потенциала соответствует логической единице, низкий – логическому нулю, длительности 1 и 0 могут быть разными.
Первые два способа представления сигнала определяют синхронную реализацию, а третий асинхронную.
| s1 |
| x1…xn С |
 1…xn С 1…xn С |
x1…xn  |
Рис. 6.1
В синхронном автомате сигнал синхронизации C обеспечивает устойчивую работу автомата и учитывается неявно. На рис. 6.1 приведен пример фрагмента графа, с явным учетом сигнала синхронизации, на нем при C = 0 не происходит изменения текущего состояния автомата.
При асинхронной реализации автомата сигнал синхронизации отсутствует, поэтому для обеспечения устойчивой работы все его состояния должны быть устойчивыми уже на абстрактном этапе синтеза.
Состояние si называется устойчивым, если при переходе в это состояние под воздействием входного символа pk автомат остается в этом состоянии до тех пор, пока на его вход не поступит символ отличный от pk (рис. 6.1).
| si |
| pk |
| pi |
| pk |
Рис. 6.2
Асинхронным автоматом называется автомат, если уже на абстрактном этапе все его состояния устойчивы.
Пример асинхронного автомата (рис. 6.3):
| s2/0 |
| s1/0 |
| s3/1 |
Рис. 6.3
Для представления асинхронного автомата используется модель автомата Мура. Графу автомата Мура (рис. 6.3) соответствует следующая таблица переходов и выходов автомата Мура (табл.6.1). В клетках этой таблицы в скобках заключены устойчивые состояния и для асинхронного автомата важно, в каком из устойчивых состояний находится автомат.
Пусть автомат находится в устойчивом состоянии s1 воздействием входного сигнала 00 и если входной сигнал изменился на 10, то для определения состояния, в которое переходит автомат необходимо:
1. двигаться по строке соответствующей текущему состоянию до столбца, отмеченного новым входным сигналом, определяется состояние, в которое должен перейти автомат;
2. двигаться по этому столбцу до устойчивого нового состояния.
Таблица 6.1
| wi | x1x2 si | ||||
| s1 | (s1) | (s1) | s2 | s3 | |
| s2 | s1 | (s2) | (s2) | (s2) | |
| s3 | s1 | s2 | s2 | (s3) |
Двигаясь по строке отмеченной символом текущего состояния s1 от столбца, отмеченного текущим сигналом 00, до столбца отмеченного новым входным сигналом 10 определяем новое состояние s3. Далее двигаться по столбцу, отмеченного новым входным сигналом 10, до устойчивого нового состояния (s3).
6.1. Синтез асинхронного автомата
Синтез асинхронного автомата отличается от синтеза синхронного автомата.
На абстрактном этапе синтеза асинхронного автомата отличие состоит в выполнении следующих дополнительных действий:
1. перекодированием входных и выходных символов для обеспечения распознавания соседних одинаковых символов;
2. при переходе от алфавитного оператора и графу автомату необходимо сделать все состояния автомата устойчивыми.
Пример необходимости перекодирования входных и выходных символов абстрактного автомата A.
Пусть P = W = {a, b, c}. Входное слово a a b b автомат перерабатывает в выходное слово b c c a. При переходе к структурному автомату символы кодируются: a = 00, b = 11, c = 10.
| b b a a |
| a c c b |
| A |
| A |
| 1 1 0 0 1 1 0 0 |
| 0 1 1 1 0 0 0 1 |
| x1 |
| x2 |
| y1 |
| y2 |
Рис. 6.4
На рис. 6.4 видно, что на уровне сигналов структурного автомата два одинаковых, подряд следующих символа, не различимы.
Необходимо расширить алфавиты: P’ = W’ = {a, a’, b, b’, c, c’}. Теперь входное слово a a’ b b’ автомат перерабатывает в выходное слово b c c’ a’ (Рис. 6.5). При переходе к структурному автомату символы кодируются: a = 000, a’ = 001, b = 110, b’ = 111, c = 100, c’ = 101.
| y1 |
| x1 |
| b’ b a’ a |
| a’ c’ c b |
| A |
| A |
| 1 1 0 0 1 1 0 0 1 0 1 0 |
| 0 1 1 1 0 0 0 1 1 1 0 0 |
| x2 |
| x3 |
| y2 |
| y3 |
Рис. 6.5
Расширение алфавита требует введение третьего разряда в код символа, но позволяет различать два одинаковых, подряд следующих символа.
На структурном этапе синтеза асинхронного автомата отличие состоит в следующем:
1. другой целью кодирования состояний автомата;
2. другой целью синтеза комбинационной схемы;
3. элементом памяти, используемым в автомате.
Задача кодирования состояний асинхронного автомата состоит в обеспечении устойчивой работы автомата, за счет устранение, так называемого, явления состязания элементов памяти.
Состязание элементов памяти
Реальные элементы памяти обладают определенной задержкой во времени срабатывания, причем величина задержки заранее не известна и зависит от технологии изготовления и от внешних факторов в процессе эксплуатации, поэтому определить соотношение задержек различных элементов памяти заранее не возможно.
| si |
| sj |
| x |
| y1y2 0 1 |
| y1y2 0 1 |
Рис. 6.6
Пусть во фрагменте графа (рис. 6.6) при переходе из si в sj элементы памяти y1 и y2 имеют задержки ∆1 и ∆2 , между ними возможны следующие соотношения, т.е. если:
1. ∆1 = ∆2 , то 01  10;
10;
2. ∆1 > ∆2 , то 01  00
00  10;
10;
3. ∆1 < ∆2 , то 01  11
11  10.
10.
Таким образом, наличие различных задержек приводит к тому, что при переходе из si в sj автомат может оказаться в некотором промежуточным незапланированном состоянии, что может привести к неправильной работе автомата.
Это явление называется состязанием элементов памяти.
В примере (рис. 6.6) могут быть три варианта соотношений. Первый вариант нереален. Во втором и третьем варианте появляются промежуточные состояния 00 и 11, именно переходы через эти состояния называются состязанием элементов памяти.
Состязания могут быть критическими и не критическими. Если состязание приводит к переходу в незапланированное устойчивое состояние, то такое состязание называется критическим.
Если же состязание приводит к переходу в незапланированное неустойчивое состояние, а затем и к переходу в нужное устойчивое состояние, то такое состязание называется некритическим.
Пример возникновения состязаний в автомате, заданным графом (рис.6.3) и таблицей переходов (табл. 6.1).
Пусть состояния закодированы следующим образом (табл. 6.2) и тогда закодированная таблица переходов имеет вид (табл. 6.3):
Таблица 6.2
| si | y1 | y2 |
| s1 | ||
| s2 | ||
| s3 |
Таблица 6.3:
| z | x1x2 y1y2 | ||||
| (00) | (00) | ||||
| (01) | (01) | (01) | |||
| (11) |
Пусть в автомате должен произойти переход по входному сигналу 10 из устойчивого состояния с кодом 00 в устойчивое состояние с кодом 11.
Если ∆1 > ∆2 , то 00  01
01  11.
11.
Состязание критическое, так как из-за такого соотношения между задержками автомат оказывается в промежуточном состоянии 01, - которое для автомата является устойчивым и перехода в состояние 11 не произойдет и это приводит неправильной работе автомата.
Если ∆1 < ∆2 , то 00  10
10  11.
11.
Состязание некритическое, так как из-за такого соотношения между задержками код в блоке памяти становится равный 10, а такой код для кодирования со
