Диаграмма Вейча для функции от 3 переменных
18.
Плавающая точка (floatingpoint) - метод представления действительных чисел, при котором число хранится в виде мантиссы и показателя степени, а значение числа вычисляется по формуле:  , где , где  - число, - число, 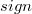 - бит, отвечающий за знак числа, - бит, отвечающий за знак числа, 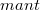 - мантисса, - мантисса, 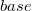 - основание степени, - основание степени, 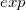 - показатель степени. - показатель степени. |
Такой метод является компромиссом между точностью и диапазоном представляемых значений. Представление чисел с плавающей точкой рассмотрим на примере чисел двойной точности (doubleprecision). Такие числа занимают в памяти два машинных слова (8 байт на 32-битных системах). Наиболее распространенное представление описано в стандарте IEEE 754.
Кроме чисел двойной точности также используются следующие форматы чисел:
§ половинной точности (halfprecision) (16 бит),
§ одинарной точности (singleprecision) (32 бита),
§ четверной точности (quadrupleprecision) (128 бит),
§ расширенной точности (extendedprecision) (80 бит).
Нормализованной называется форма представления числа, при которой абсолютное значение мантиссы десятичного числа лежит на полуинтервале  , а двоичного на полуинтервале
, а двоичного на полуинтервале 
Число не нормализовано, если старшая цифра мантиссы равна нулю, т.е.  .
.
q – основание системы счисления
m– мантисса числа
21.Стандарт IEEE 754
IEEE 754 — широко распространённый стандарт, описывающий формат представления чисел с плавающей точкой. Используется в программных и аппаратных реализациях арифметических. Форматы стандарта:
· Число половинной точности (разрядная сетка 2 байта)
Представление мантиссы
В записи числа используется нормализованная мантисса. Но реализация нормализации отличается от общей идеи. Дело в том, что в традиционном нормализованном числе единица в старшем бите мантиссы есть всегда. Следовательно, ее можно не сохранять, но «подразумевать». Поэтому стандарт определяет мантиссу следующим образом: она состоит из неявного бита, который всегда равен 1, двоичной точки и остальных разрядов. Получается, что мантисса охватывает диапазон чисел [1, 2). Мантисса представляется в прямом коде.
При выполнении арифметических операций с мантиссами не забывать про мнимые единицы!
Представление порядка
Порядок числа записывается в смещенном коде, т.е., к нему прибавляется фиксированное число, чтобы порядок был всегда неотрицательным. Это упрощает выполнения операций над порядками, избавляет от знакового разряда порядка.
Истинный порядок может быть и положительным, и отрицательным. Все доступные разряды порядка разделяются поровну между его положительными и отрицательными значениями. При выполнении арифметических операций процессор учитывает сдвиг.
Одна комбинация резервируется для специальных нужд.
Ограничения точности для целых чисел
· Целые между 0 и 2047 представляются точно
· Целые между 2048 и 4095 округляются вниз до кратного 2 (четному числу)
· Целые между 4096 и 8191 округляются вниз до кратного 4
· Целые между 8192 и 16383 округляются вниз до кратного 8
· Целые между 16384 и 32767 округляются вниз до кратного 16
· Целые между 32768 и 65535 округляются вниз до кратного 32
24.Логические основы вычислительной техники – это раздел информатики, занимающийся вопросами анализа и синтеза основных устройств цифровой схемотехники.
Комбинационные схемы 𝑦=𝑓(𝑥1,…,𝑥𝑛):
· Элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, ИСКЛ-ИЛИ
· Мультиплексоры и демультиплексоры
· Шифраторы и дешифраторы
· Компараторы
· Комбинационные сумматоры
Под комбинационной схемой (КС) понимают схему, комбинация сигналов на выходе которой в любоймомент времени однозначно определяется комбинацией сигналов на её входе.
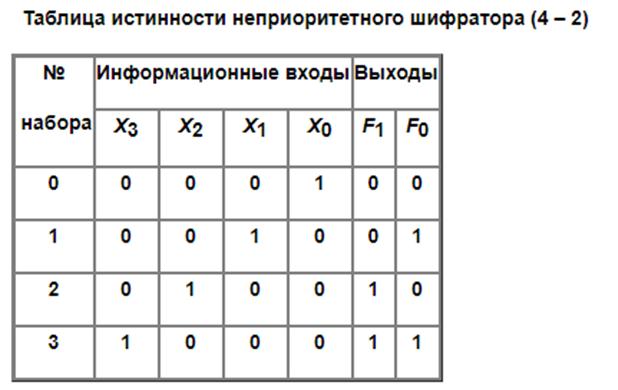
Примером КС могут служить разнообразные шифраторы, дешифраторы, преобразователи кодов, сумматоры и целый ряд других схем, не содержащих элементов памяти.
КС
В КС совокупность входных сигналов y в любой момент времени определена входными сигналами x, поступающими на входы в тот же самый момент времени. Реализуемый способ работы обработки информации называется комбинационным, т.к. результат обработки зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входной информации.
Закон функционирования КС определен, если задано соответствие между ее входными и выходными словами. Это соответствие может быть задано в виде таблицы или с помощью булевых функций.
Простые цифровые автоматы 𝑦(𝑡+1)=𝑓(𝑥1,…,𝑥𝑛,𝑦(𝑡)):
· Триггеры
· Регистры
· Счетчики
Цифровой автомат (ЦА) – это условная, формальная модель любого информационного устройства дискретного действия. Модель предназначена для представления устройства на логическом уровне, т.е. в ней не допускается использование каких-либо физических характеристик процессов, происходящих при работе реального устройства.
ЦА (базой является КС)
ЦА в отличие от КС имеет некоторое конечное число различных внутренних состояний. Под воздействием входного слова X ЦА переходит из одного состояния в другое и выдает при этом выходное слово.
Выходное слово в такте определяется выходным словом, поступившим в этот такт на вход автомата, и внутренним состоянием автомата, которое явилось результатом воздействия на автомат входных слов в предыдущем такте.
Комбинация входного слова и текущего состояния автомата в данном такте определяет не только выходное слово, но и состояние, в котором автомат перейдет к началу следующего такта.
27.Конъюнкт – конъюнкция некоторых переменных или их отрицаний.
Дизъюнкт – дизъюнкция некоторых переменных или их отрицаний.
Если конъюнкт (дизъюнкт) состоит из всех переменных функции или их отрицаний, где каждая переменная участвует лишь единожды, то такой конъюнкт (дизъюнкт) называется совершенным.
Минтерм (конституента единицы) – это логическая функция, принимающая значение истина только на одном наборе значений своих аргументов. Формальная записьминтерма – это конъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от 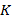 переменных есть
переменных есть  минтермов. Минтерм – это совершенный конъюнкт.
минтермов. Минтерм – это совершенный конъюнкт.
Макстерм (конституента нуля) – это логическая функция, принимающая значение ложь только на одном наборе значений своих аргументов. Формальная записьмакстерама – это дизъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от 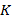 переменных есть
переменных есть  макстермов. Макстерм – это совершенный дизъюнкт.
макстермов. Макстерм – это совершенный дизъюнкт.
Дизъюнктивная нормальная форма (ДНФ) – дизъюнкция конечного числа конъюнктов. Совершенная ДНФ(СДНФ)– дизъюнкция совершенных конъюнктов (т.е. минтермов). Любая логическая функция, не являющаяся логическим нулем, имеет только одну СДНФ.
Конъюнктивная нормальная форма (КНФ) – конъюнкция конечного числа дизъюнктов. Совершенная КНФ (СКНФ)– конъюнкция совершенных дизъюнктов (т.е. макстермов). Любая логическая функция, не являющаяся логической единицей, имеет только одну СКНФ.
30.Задача минимизации логической функции заключается в том, чтобы найти наиболее компактное ее представление в виде нормальной формы минимальной сложности – минимальной дизъюнктивной нормальной формы (МДНФ) или минимальной конъюнктивной нормальной формы (МКНФ).
Минимальная нормальная форма – это нормальная форма, содержащая минимальное количество переменных, использованных с отрицанием или без.
Минимальная дизъюнктивная нормальная форма – это дизъюнкция минимального числа конъюнкций переменных, взятых с отрицанием или без.
Минимальная конъюнктивная нормальная форма – это конъюнкция минимального числа дизъюнкций переменных, взятых с отрицанием или без.
Метод эквивалентных логических преобразований
Получение МДНФ (МКНФ) через упрощение СДНФ (СКНФ) по правилам преобразования.
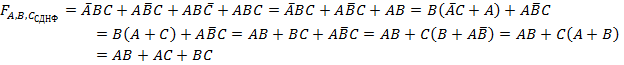
33.Графический способ минимизации логических функций. Работает на основе операций склеивания и поглощения. Представляет собой особым образом переупорядоченную таблицу истинности.
Операция склеивания осуществляется между двумя совершенными конъюнктами (дизъюнктами), у которых совпадают все литералы, кроме одного. По правилам склеивания совпадающие литералы выносятся за скобки, а оставшиеся подвергнуть склейке.
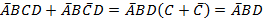
В диаграмме Вейча ячейки таблицы истинности сгруппированы таким образом, что переход из одной ячейки в другую по вертикали или горизонтали связан с изменением значения только одной переменной. В результате этого наборы, между которыми возможно склеивание, получаются сгруппированными вместе и их легко заметить. Метод Вейча подходит для минимизации функций до 7 переменных. При большем количестве теряются достоинства метода.
Интервал логической функции от 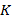 переменных – это такое множество наборов значений переменных, что:
переменных – это такое множество наборов значений переменных, что:
· Значение функции на этом множестве постоянно;
· Мощность (величина, размер интервала) этого множества равна  ,
, 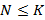 ;
;
· 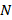 является количеством переменных, которые упрощаются на этом множестве, а оставшихся (
является количеством переменных, которые упрощаются на этом множестве, а оставшихся (  ) переменных достаточно для описания логической функции на данном множестве;
) переменных достаточно для описания логической функции на данном множестве;
· Если 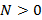 , то каждый следующий набор отличается от предыдущего значением только одной переменной.
, то каждый следующий набор отличается от предыдущего значением только одной переменной.
Типы интервалов
| * | * | * | * | * | |||
| * | * | * | * | ||||
| * | * | ||||||
| * | * | * | * | ||||
| * | * | * | * | ||||
| * |
Интервал размера 1
Вырожденный случай. Упрощения не происходит. Интервал может встречаться на любых диаграммах.
Интервал размера 2
Упрощается одна переменная. Интервалы могут встречаться на любых диаграммах.
Интервал размера 4
Упрощается 2 переменных. Некоторые интервалы встречаются, начиная с диаграммы Вейча для функции от 3 переменных.
Интервалы размером 8
Упрощается 3 переменных. Некоторые интервалы встречаются, начиная с диаграммы Вейча для функции от 4 переменных.
Алгоритм минимизации
1. Нарисовать исходную таблицу диаграммы и сделать ее разметку в зависимости от количества переменных функции.
2. Заполнить таблицу значениями функции с учетом цели минимизации (удобно выписывать только 1 для МДНФ и только 0 для МКНФ).
3. Выделить контурами интервалы из единиц (МДНФ) или нулей (МКНФ), соблюдая следующие правила:
a. Необходимо стараться выделить максимально большие интервалы;
b. Каждый новый интервал должен содержать хотя бы одно значение, принадлежащее только ему;
c. Необходимо выделить минимально возможное количество интервалов.
4. Выписать формулу МДНФ (МКНФ), для чего:
a. Для каждого интервала выписать конъюнкт (дизъюнкт), в который будут входить только те переменные или их отрицания, которые сохраняют свое значение на интервале. Остальные переменные упростятся.
b. Соединить выписанные конъюнкты (дизъюнкты) через дизъюнкцию (конъюнкцию).
Традиционное применение
· В составе схем управления другими устройствами для последовательной подачи разрешающих сигналов;
· В составе схем преобразователей кодов;
· Для реализации логических функций.
Традиционное применение
· «Ленивая» реализация логических функций, когда минимизацией можно пренебречь. Удобно для разработчика, но приводит к дополнительным затратам.
· В качестве коммутатора  к 1:
к 1:
o Для преобразования параллельного входа в последовательный;
o Для поочередного подключения многих источников информации к одному потребителю.
Традиционное использование
· Получение кодов нажатых клавиш;
· В составе преобразователей кодов.

48.Сумматор – цифровое устройство, предназначенное для сложения двух чисел в разных кодах. Если используются специальные коды, то на сумматоре можно выполнять вычитание.
57.
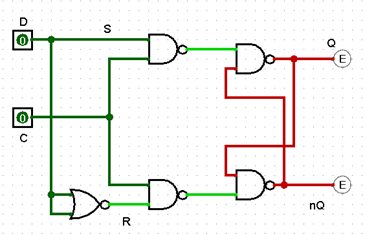
Триггер-задержка – хранит предыдущее состояние до прихода очередного синхроимпульса.
| D | Q(t) | Q(t+1) |
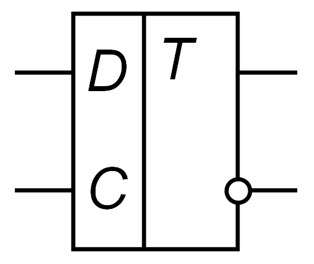
D-триггер — запоминает состояние входа и выдаёт его на выход. D-триггеры имеют, как минимум, два входа: информационный D и синхронизации С. Вход синхронизации С может быть статическим (потенциальным) и динамическим. У триггеров со статическим входом С информация записывается в течение времени, при котором уровень сигнала C=1. В триггерах с динамическим входом С информация записывается только в течение перепада напряжения на входе С. В таком триггере информация на выходе может быть задержана на один такт по отношению к входной информации. Так как информация на выходе остаётся неизменной до прихода очередного импульса синхронизации, D-триггер называют также триггером с запоминанием информации или триггером-защёлкой. Рассуждая чисто теоретически, парафазный (двухфазный) D-триггер можно образовать из любых RS- или JK-триггеров, если на их входы одновременно подавать взаимно инверсныесигналы.
60.
Регистром называется цифровой автомат, реализованный на триггерах, основным назначением которого является прием двоичной информации, временное хранение двоичной информации и выдача информации потребителю.
Этот минимум операций выполняет простейший регистр, который называется регистром хранения. Запись и выдача информации осуществляется на все разряды одновременно (т.е. в параллельном коде).
Усовершенствованный регистр (сдвиговый) может также выполнять операцию сдвига информации вправо и влево (умножение или деление на 2).
Благодаря операции сдвига становятся возможными различные способы приема и выдачи информации:
· Параллельный прием
· Параллельная выдача
· Последовательный прием
· Последовательная выдача
Таким образом, сдвиговый регистр может:
· Преобразовывать последовательный код в параллельный и наоборот
· Быстро выполнять операции умножения и деления на 2
Регистры классифицируют по:
· Количеству разрядов
· Триггерам, на которых они реализованы
· Способу приема и выдачи данных
o Параллельные (простейшие триггеры хранения)
o Последовательные (последовательный прием, последовательная выдача)
Параллельно-последовательные (универсальный сдвиговый регистр).
Сдвиговый регистр
Триггеры сдвигового регистра связаны между собой цепями переноса, что позволяет одновременно переносить содержимое отдельного триггера регистра в соседний триггер, осуществляя операцию сдвига. Сдвиг характеризуется:
· Направлением – влево или вправо
· Типом
o Логический (в освободившийся крайний триггер заносится 0)
o Арифметический (содержимое регистра понимается как число в дополнительном коде. При сдвиге влево справа появляется 0, при сдвиге вправо слева дублируется предыдущее значение)
o Циклический (вытесняемое из регистра значение заносится в освободившийся триггер на другом конце)
63.
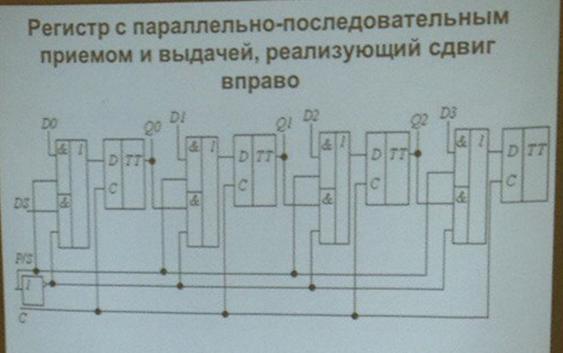
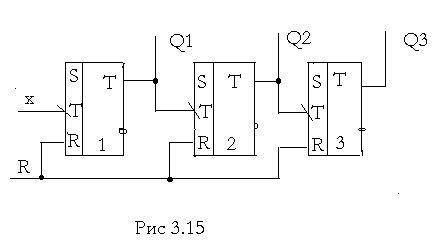 66.
66.
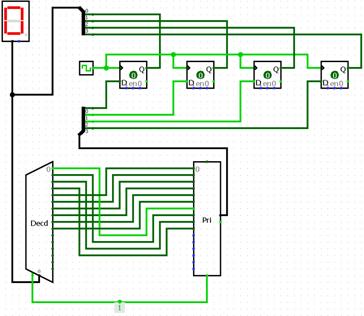
трехразрядный суммирующий двоичный счетчик на Т-триггерах с последовательным переносом
| № состояния | 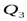 | 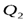 | 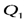 |
Счетчики с последовательным переносом имеют большие времена задержки и их основное применение – системы управления с относительно невысоким быстродействием.
69.
72.
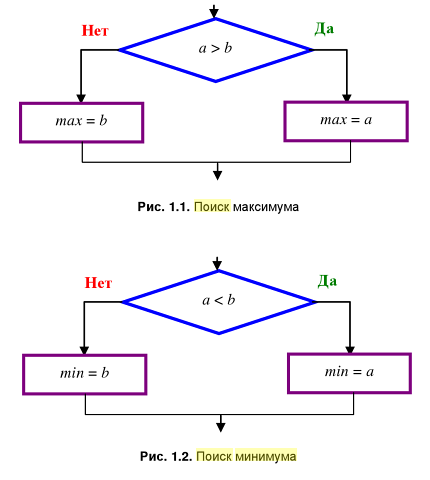
Минимум
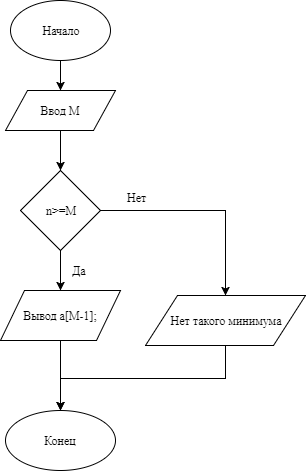
int M;
sort(n, a);
out_arr(n, a);
cout<<endl;
bool flag;
do{
flag = true;
cout<<"Введите номер M-ый минимум"<<endl;
try {
string s;
cin>> s;
M = stoi(s);
if (n>=M && M>0)
cout<<"M-ыйминимум "<< a[M - 1] <<endl;
else
throw 1;
}
catch (...)
{
cout<<"Такогоминимуманет"<<endl;
cout<<"Введитезаново"<<endl;
flag = false;
}
} while (!flag);
system("PAUSE");
break;
}
Максимум
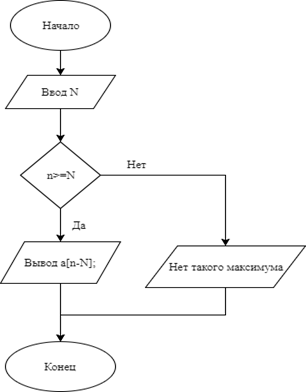
int N;
sort(n, a);
out_arr(n, a);
cout<<endl;
bool flag;
do{
flag = true;
cout<<"ВведитеномерN-максимума"<<endl;
try {
string s;
cin>> s;
N = stoi(s);
if (n >= N && N > 0)
cout<<"N-ыймаксимум "<< a[n - N] <<endl;
else
throw 1;
}
catch(...)
{
cout<<"Такогомаксимуманет"<<endl;
cout<<"Введитезаново"<<endl;
flag = false;
}
} while (!flag);
system("PAUSE");
break;
}
75.
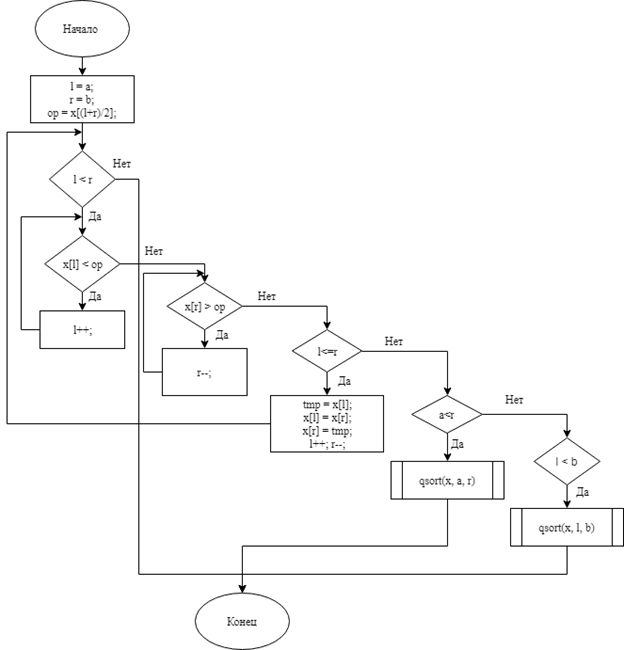
voidqsort(int *x, inta, intb)
{
int op;
int left = a, right = b;
op = x[(left + right) / 2];
do
{
while (x[left] < op)
left++;
while (x[right] > op)
right--;
if (left <= right)
{
inttmp = x[left];
x[left] = x[right];
x[right] = tmp;
left++;
right--;
}
} while (left<right);
if (a<right)
qsort(x, a, right);
if (left<b)
qsort(x, left, b);
}
18.
Плавающая точка (floatingpoint) - метод представления действительных чисел, при котором число хранится в виде мантиссы и показателя степени, а значение числа вычисляется по формуле:  , где , где  - число, - число, 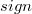 - бит, отвечающий за знак числа, - бит, отвечающий за знак числа, 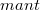 - мантисса, - мантисса, 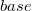 - основание степени, - основание степени, 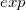 - показатель степени. - показатель степени. |
Такой метод является компромиссом между точностью и диапазоном представляемых значений. Представление чисел с плавающей точкой рассмотрим на примере чисел двойной точности (doubleprecision). Такие числа занимают в памяти два машинных слова (8 байт на 32-битных системах). Наиболее распространенное представление описано в стандарте IEEE 754.
Кроме чисел двойной точности также используются следующие форматы чисел:
§ половинной точности (halfprecision) (16 бит),
§ одинарной точности (singleprecision) (32 бита),
§ четверной точности (quadrupleprecision) (128 бит),
§ расширенной точности (extendedprecision) (80 бит).
Нормализованной называется форма представления числа, при которой абсолютное значение мантиссы десятичного числа лежит на полуинтервале  , а двоичного на полуинтервале
, а двоичного на полуинтервале 
Число не нормализовано, если старшая цифра мантиссы равна нулю, т.е.  .
.
q – основание системы счисления
m– мантисса числа
21.Стандарт IEEE 754
IEEE 754 — широко распространённый стандарт, описывающий формат представления чисел с плавающей точкой. Используется в программных и аппаратных реализациях арифметических. Форматы стандарта:
· Число половинной точности (разрядная сетка 2 байта)
Представление мантиссы
В записи числа используется нормализованная мантисса. Но реализация нормализации отличается от общей идеи. Дело в том, что в традиционном нормализованном числе единица в старшем бите мантиссы есть всегда. Следовательно, ее можно не сохранять, но «подразумевать». Поэтому стандарт определяет мантиссу следующим образом: она состоит из неявного бита, который всегда равен 1, двоичной точки и остальных разрядов. Получается, что мантисса охватывает диапазон чисел [1, 2). Мантисса представляется в прямом коде.
При выполнении арифметических операций с мантиссами не забывать про мнимые единицы!
Представление порядка
Порядок числа записывается в смещенном коде, т.е., к нему прибавляется фиксированное число, чтобы порядок был всегда неотрицательным. Это упрощает выполнения операций над порядками, избавляет от знакового разряда порядка.
Истинный порядок может быть и положительным, и отрицательным. Все доступные разряды порядка разделяются поровну между его положительными и отрицательными значениями. При выполнении арифметических операций процессор учитывает сдвиг.
Одна комбинация резервируется для специальных нужд.
Ограничения точности для целых чисел
· Целые между 0 и 2047 представляются точно
· Целые между 2048 и 4095 округляются вниз до кратного 2 (четному числу)
· Целые между 4096 и 8191 округляются вниз до кратного 4
· Целые между 8192 и 16383 округляются вниз до кратного 8
· Целые между 16384 и 32767 округляются вниз до кратного 16
· Целые между 32768 и 65535 округляются вниз до кратного 32
24.Логические основы вычислительной техники – это раздел информатики, занимающийся вопросами анализа и синтеза основных устройств цифровой схемотехники.
Комбинационные схемы 𝑦=𝑓(𝑥1,…,𝑥𝑛):
· Элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, ИСКЛ-ИЛИ
· Мультиплексоры и демультиплексоры
· Шифраторы и дешифраторы
· Компараторы
· Комбинационные сумматоры
Под комбинационной схемой (КС) понимают схему, комбинация сигналов на выходе которой в любоймомент времени однозначно определяется комбинацией сигналов на её входе.
Примером КС могут служить разнообразные шифраторы, дешифраторы, преобразователи кодов, сумматоры и целый ряд других схем, не содержащих элементов памяти.
КС
В КС совокупность входных сигналов y в любой момент времени определена входными сигналами x, поступающими на входы в тот же самый момент времени. Реализуемый способ работы обработки информации называется комбинационным, т.к. результат обработки зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входной информации.
Закон функционирования КС определен, если задано соответствие между ее входными и выходными словами. Это соответствие может быть задано в виде таблицы или с помощью булевых функций.
Простые цифровые автоматы 𝑦(𝑡+1)=𝑓(𝑥1,…,𝑥𝑛,𝑦(𝑡)):
· Триггеры
· Регистры
· Счетчики
Цифровой автомат (ЦА) – это условная, формальная модель любого информационного устройства дискретного действия. Модель предназначена для представления устройства на логическом уровне, т.е. в ней не допускается использование каких-либо физических характеристик процессов, происходящих при работе реального устройства.
ЦА (базой является КС)
ЦА в отличие от КС имеет некоторое конечное число различных внутренних состояний. Под воздействием входного слова X ЦА переходит из одного состояния в другое и выдает при этом выходное слово.
Выходное слово в такте определяется выходным словом, поступившим в этот такт на вход автомата, и внутренним состоянием автомата, которое явилось результатом воздействия на автомат входных слов в предыдущем такте.
Комбинация входного слова и текущего состояния автомата в данном такте определяет не только выходное слово, но и состояние, в котором автомат перейдет к началу следующего такта.
27.Конъюнкт – конъюнкция некоторых переменных или их отрицаний.
Дизъюнкт – дизъюнкция некоторых переменных или их отрицаний.
Если конъюнкт (дизъюнкт) состоит из всех переменных функции или их отрицаний, где каждая переменная участвует лишь единожды, то такой конъюнкт (дизъюнкт) называется совершенным.
Минтерм (конституента единицы) – это логическая функция, принимающая значение истина только на одном наборе значений своих аргументов. Формальная записьминтерма – это конъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от 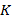 переменных есть
переменных есть  минтермов. Минтерм – это совершенный конъюнкт.
минтермов. Минтерм – это совершенный конъюнкт.
Макстерм (конституента нуля) – это логическая функция, принимающая значение ложь только на одном наборе значений своих аргументов. Формальная записьмакстерама – это дизъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от 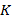 переменных есть
переменных есть  макстермов. Макстерм – это совершенный дизъюнкт.
макстермов. Макстерм – это совершенный дизъюнкт.
Дизъюнктивная нормальная форма (ДНФ) – дизъюнкция конечного числа конъюнктов. Совершенная ДНФ(СДНФ)– дизъюнкция совершенных конъюнктов (т.е. минтермов). Любая логическая функция, не являющаяся логическим нулем, имеет только одну СДНФ.
Конъюнктивная нормальная форма (КНФ) – конъюнкция конечного числа дизъюнктов. Совершенная КНФ (СКНФ)– конъюнкция совершенных дизъюнктов (т.е. макстермов). Любая логическая функция, не являющаяся логической единицей, имеет только одну СКНФ.
30.Задача минимизации логической функции заключается в том, чтобы найти наиболее компактное ее представление в виде нормальной формы минимальной сложности – минимальной дизъюнктивной нормальной формы (МДНФ) или минимальной конъюнктивной нормальной формы (МКНФ).
Минимальная нормальная форма – это нормальная форма, содержащая минимальное количество переменных, использованных с отрицанием или без.
Минимальная дизъюнктивная нормальная форма – это дизъюнкция минимального числа конъюнкций переменных, взятых с отрицанием или без.
Минимальная конъюнктивная нормальная форма – это конъюнкция минимального числа дизъюнкций переменных, взятых с отрицанием или без.
Метод эквивалентных логических преобразований
Получение МДНФ (МКНФ) через упрощение СДНФ (СКНФ) по правилам преобразования.
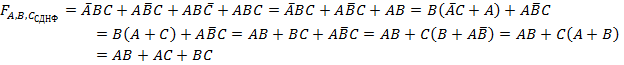
33.Графический способ минимизации логических функций. Работает на основе операций склеивания и поглощения. Представляет собой особым образом переупорядоченную таблицу истинности.
Операция склеивания осуществляется между двумя совершенными конъюнктами (дизъюнктами), у которых совпадают все литералы, кроме одного. По правилам склеивания совпадающие литералы выносятся за скобки, а оставшиеся подвергнуть склейке.
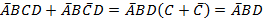
В диаграмме Вейча ячейки таблицы истинности сгруппированы таким образом, что переход из одной ячейки в другую по вертикали или горизонтали связан с изменением значения только одной переменной. В результате этого наборы, между которыми возможно склеивание, получаются сгруппированными вместе и их легко заметить. Метод Вейча подходит для минимизации функций до 7 переменных. При большем количестве теряются достоинства метода.
Интервал логической функции от 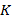 переменных – это такое множество наборов значений переменных, что:
переменных – это такое множество наборов значений переменных, что:
· Значение функции на этом множестве постоянно;
· Мощность (величина, размер интервала) этого множества равна  ,
, 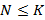 ;
;
· 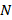 является количеством переменных, которые упрощаются на этом множестве, а оставшихся (
является количеством переменных, которые упрощаются на этом множестве, а оставшихся (  ) переменных достаточно для описания логической функции на данном множестве;
) переменных достаточно для описания логической функции на данном множестве;
· Если 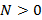 , то каждый следующий набор отличается от предыдущего значением только одной переменной.
, то каждый следующий набор отличается от предыдущего значением только одной переменной.
Типы интервалов
| * | * | * | * | * | |||
| * | * | * | * | ||||
| * | * | ||||||
| * | * | * | * | ||||
| * | * | * | * | ||||
| * |
Интервал размера 1
Вырожденный случай. Упрощения не происходит. Интервал может встречаться на любых диаграммах.
Интервал размера 2
Упрощается одна переменная. Интервалы могут встречаться на любых диаграммах.
Интервал размера 4
Упрощается 2 переменных. Некоторые интервалы встречаются, начиная с диаграммы Вейча для функции от 3 переменных.
Интервалы размером 8
Упрощается 3 переменных. Некоторые интервалы встречаются, начиная с диаграммы Вейча для функции от 4 переменных.
Алгоритм минимизации
1. Нарисовать исходную таблицу диаграммы и сделать ее разметку в зависимости от количества переменных функции.
2. Заполнить таблицу значениями функции с учетом цели минимизации (удобно выписывать только 1 для МДНФ и только 0 для МКНФ).
3. Выделить контурами интервалы из единиц (МДНФ) или нулей (МКНФ), соблюдая следующие правила:
a. Необходимо стараться выделить максимально большие интервалы;
b. Каждый новый интервал должен содержать хотя бы одно значение, принадлежащее только ему;
c. Необходимо выделить минимально возможное количество интервалов.
4. Выписать формулу МДНФ (МКНФ), для чего:
a. Для каждого интервала выписать конъюнкт (дизъюнкт), в который будут входить только те переменные или их отрицания, которые сохраняют свое значение на интервале. Остальные переменные упростятся.
b. Соединить выписанные конъюнкты (дизъюнкты) через дизъюнкцию (конъюнкцию).
Диаграмма Вейча для функции от 3 переменных
МКНФ:
 | 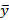 | |||
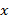 | 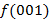 |  |  | 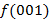 |
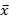 |  | 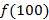 | 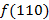 | 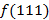 |
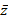 |  | 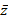 |
36.Логический базис:
· Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.
· Полная система функций называется базисом, если она перестаёт быть полной при исключении из неё любого элемента.
