Решение задач с поразрядными операциями

Для решения этих задач удобно применять метод, предложенный А.В. Здвижковой (г. Армавир) и обоснованный автором[2]. Введём обозначения

Это означает, что если истинно , то это равносильно тому, что истинно . Для сокращения записи вместо будем писать просто .

Пусть в двоичной записи числа K бит с номером i, обозначаемый как k_i, равен 1. Если при этом для некоторого x выполнено условие , то соответствующий i-й бит в двоичной записи числа x равен нулю, так как должно выполняться условие .

Для преобразования выражений полезно следующее свойство:

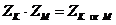
где «or» означает поразрядную дизъюнкцию между двумя натуральными числами. Для доказательства предположим, что в двоичной записи числа K биты с номерами i₁, i₂, …, i_q равны 1, а остальные равны 0; а в двоичной записи числа M биты с номерами j₁, j₂, …, j_p равны 1, а остальные равны 0. Истинность выражения в левой части означает, что все биты числа x, входящие во множества B_K = {i₁, i₂, …, i_q} и B_M = {j₁, j₂, …, j_p} одновременно равны нулю. Поэтому любая комбинация битов из этих множеств тоже равна нулю. Это справедливо, в том числе, и для множества, которое представляет собой объединение множеств B_K и B_M, то есть, для множества единичных битов числа K or M.

Самый важный результат можно сформулировать так:

Условие истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

Доказательство. Пусть в двоичной записи числа K биты с номерами i₁, i₂, …, i_q равны 1, а остальные равны 0. Пусть также истинно для некоторого x, это значит, что в числе x биты с теми же номерами – нулевые. Если все единичные биты двоичной записи числа M входят во множество B_K = {i₁, i₂, …, i_q}, то истинно и высказывание , а следовательно – высказывание (1 ® 1 = 1). Если же хотя бы один бит двоичной записи числа M не входит во множество B_K (пусть это будет бит с номером j), то для тех х, у которых все биты из множества B_K нулевые, а бит j равен 1, выполняется , но не выполняется , так что высказывание ложно.

Для упрощения выражений полезен следующий результат:

Условие при любых натуральных K, M и N ложно для некоторых натуральных значений x.

Идея доказательства состоит в том, чтобы представить импликацию в виде произведения двух импликаций:

.

Вторая импликация в правой части ложна хотя бы для некоторых x, поскольку из того, что некоторые биты числа x равны нулю (выполняется ) совершенно не следует, что какие-то другие (или те же самые) биты того же числа ненулевые (выполняется ). Строгое доказательство дано в статье, ссылка на которую приведена в сноске на предыдущей странице.

Метод, предложенный А.В. Здвижковой заключается в следующем:

1) упростить заданное выражение, сведя его к импликации, в которой нет инверсий

2) применить полученные выше результаты для нахождения всех подходящих значений неизвестного числа a, включая минимальное и максимальное значения.

Этот же метод можно применить и в том случае, когда результат поразрядной операции «И» сравнивается не с нулём, а с другими числами. Например, рассмотрим выражение R = (x &125= 5). Переведём числа в двоичную систему:

6 5 4 3 2 1 0

125 = 1111101₂

5 = 101₂.

Истинность R означает, что

1) биты числа x с номерами 3, 4, 5 и 6 равны 0;

2) биты числа x с номерами 0 и 2 равны 1.

С учётом введённых выше обозначений можно записать эквивалентное условие:

R = (x &125= 5) Û .

Применяя операцию «НЕ» к этому выражению, получаем

= (x &125¹ 5) Û Û .

В общем виде для чисел b и c, таких, что множество единичных битов числа c входит во множество единичных битов числа b, имеем

R = (x & b = c) Û

= (x & b ¹ c) Û .

где c­₁, c­₂, …, c­_q – степени числа 2, которые соответствуют единичным битам числа c. Например, для
c = 5 = 101₂ имеем c­₁ = 2² = 4, c­₂ = 2⁰ = 1.

Пример задания:

Р-25. Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число a, такое что выражение

( x &125¹ 1) Ú ((x & 34 = 2) ® (x & a = 0))